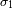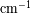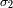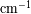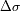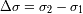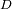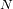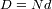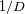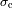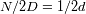Objetivos
Objetivos
Mostrar cómo los parámetros de un interferograma tienen que ser elegidos para optimizar su
adquisición. Se sobreentiende que optimizado significa respectando la resolución espectral deseada.
Los parámetros del espectro
La interferometría consiste en conseguir una información espectral con unos elementos deseados. Los
parámetros del interferograma tienen que obedecer a este principio.
Un espectro queda esencialmente caracterizado por:
- El intervalo espectral
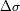 : corresponde al filtro de entrada. En la práctica se elige dentro de una lista propuesta.
: corresponde al filtro de entrada. En la práctica se elige dentro de una lista propuesta.
- La resolución espectral
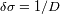 que hay que ajustar con una de las propiedades del interferograma.
que hay que ajustar con una de las propiedades del interferograma.
Los parámetros del interferograma
Criterios de elección de los parámetros del interferograma
Por principio, la espectrometría de transformada de Fourier requiere la selección de una región
espectral que no sea muy ancha. Por ello se tiene que utilizar un filtro adecuado para hacer
esta selección alrededor de la lineas que se pretende estudiar estudiar. Este requisito se puede
entender de dos maneras: (a) del punto de vista instrumental, un filtro ancho producirá un
color plano muy rápidamente, impidiendo la extracción de cualquier información. (b) del punto
de vista del espacio de Fourier, se requiere trabajar en una región limitada del espectro para
que un muestreo limitado (es decir un intervalo espectral limitado) sea suficiente para recobrar
toda la información espectral.
Intervalo espectral libre
Se denota
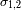
a los limites inferior y superior respectivamente de la banda pasante útil. El ancho de la banda
pasante
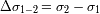
determina el dominio de los números de onda en el cual no debe haber
confusión espectral.
Dicho de otra manera, el sampling tiene que asegurar una frecuencia de corte espacial
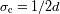
de tal manera que el ancho espectral
![[s1,s2]](../../../../images/fourier/images-TeX4ht/fourier109x.png)
del filtro sea contenido
por el intervalo espectral libre
![[nsc,(n + 1)sc]](../../../../images/fourier/images-TeX4ht/fourier110x.png)
:
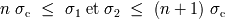
con

un numero entero natural.
Elección de los parámetros del interferograma en la práctica

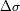 : corresponde al filtro de entrada. En la práctica se elige dentro de una lista propuesta.
: corresponde al filtro de entrada. En la práctica se elige dentro de una lista propuesta.
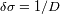 que hay que ajustar con una de las propiedades del interferograma.
que hay que ajustar con una de las propiedades del interferograma.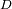 .
.
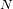 entre la diferencia de camino nula y máxima
entre la diferencia de camino nula y máxima
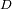 , equidistantes de
, equidistantes de
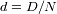 .
.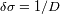
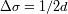
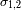 a los limites inferior y superior respectivamente de la banda pasante útil. El ancho de la banda
pasante
a los limites inferior y superior respectivamente de la banda pasante útil. El ancho de la banda
pasante
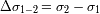 determina el dominio de los números de onda en el cual no debe haber confusión espectral.
determina el dominio de los números de onda en el cual no debe haber confusión espectral.
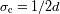 de tal manera que el ancho espectral
de tal manera que el ancho espectral
![[s1,s2]](../../../../images/fourier/images-TeX4ht/fourier109x.png) del filtro sea contenido por el intervalo espectral libre
del filtro sea contenido por el intervalo espectral libre
![[nsc,(n + 1)sc]](../../../../images/fourier/images-TeX4ht/fourier110x.png) :
:
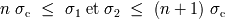
 un numero entero natural.
un numero entero natural.
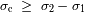 . Si se supone la diferencia de camino máxima
. Si se supone la diferencia de camino máxima
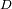 fijada (y con ello la resolución), se puede elegir el numero de puntos óptimo
fijada (y con ello la resolución), se puede elegir el numero de puntos óptimo
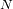 que resulta de las 2 condiciones anteriores.
que resulta de las 2 condiciones anteriores.
 y
y
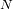 tienen que ser enteros, sus soluciones reales deben verificar:
tienen que ser enteros, sus soluciones reales deben verificar:
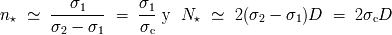
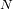 y
y
 que aseguran de manera óptima:
que aseguran de manera óptima:

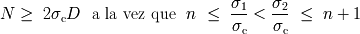
 y
y
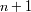 aseguran la validez del intervalo espectral
aseguran la validez del intervalo espectral
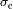 definido por
definido por
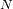 .
.