 Requisitos previos
Requisitos previos
Nociones elemental de estadística.
 Objetivos
Objetivos
La definición de un ruido se basa en sus propiedades estadísticas. Esta página repasa nociones simples de
estadística, distinguiendo las
leyes de probabilidad, sus
pruebas, y la
estimación de sus parámetros
estadísticos.
Ley de probabilidad
La ley de probabilidad de una variable aleatoria

viene dada por
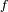
su densidad de probabilidad o
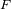
su función de repartición
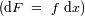
.
En los momentos centrados asociados, el promedio

y la desviación estándar

son definidos como:
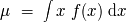
y
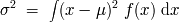
(
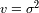
es la varianza).
Una ley estadística tiene propiedades peculiares que caracterizan tal o tal fenómeno. Por ejemplo la ley
de
Poisson
(discreta) describe bien la llegada de sucesos independientes. Otro ejemplo, la ley de
Gauss
describe la suma de una gran cantidad de fenómenos independientes...

Realizaciones
La realización de una ley de probabilidad es aleatoria: 6 tiradas de un dado no conducirán a la
obtención de cada cifra. Pero cuanto mayor sea la cantidad de
pruebas
más se parecerá la observación de éstas a la ley de probabilidad.
Estimaciones
En la practica, se tiene que distinguir por una parte el valor promedio

de la densidad de probabilidad y su medida

. Siendo
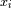
las pruebas aleatorias, sólo tenemos acceso a :
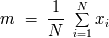
Y no hay ninguna razón para que
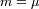
. Esto ocurre cada vez más en cuanto
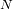
se hace muy grande.
La varianza

se puede medir por:
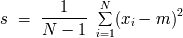
con
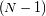
en el denominador porque

ya fue conseguido con las
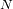
medidas y sólo quedan
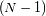
valores independientes para estimar

.
La desviación entre

y

vale típicamente

.

 viene dada por
viene dada por
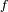 su densidad de probabilidad o
su densidad de probabilidad o
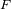 su función de repartición
su función de repartición
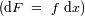 .
.
 y la desviación estándar
y la desviación estándar
 son definidos como:
son definidos como:
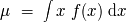
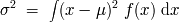
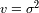 es la varianza).
es la varianza).
 de la densidad de probabilidad y su medida
de la densidad de probabilidad y su medida
 . Siendo
. Siendo
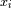 las pruebas aleatorias, sólo tenemos acceso a :
las pruebas aleatorias, sólo tenemos acceso a :
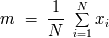
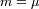 . Esto ocurre cada vez más en cuanto
. Esto ocurre cada vez más en cuanto
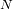 se hace muy grande.
se hace muy grande.
 se puede medir por:
se puede medir por:
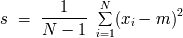
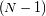 en el denominador porque
en el denominador porque
 ya fue conseguido con las
ya fue conseguido con las
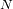 medidas y sólo quedan
medidas y sólo quedan
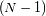 valores independientes para estimar
valores independientes para estimar
 .
.
 y
y
 vale típicamente
vale típicamente
 .
.