 Objetivos
Objetivos
Utilizar la TF para buscar fenómenos periódicos.
Medida
Si se graba una serie temporal de
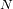
señales, durante un tiempo
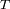
, el análisis por transformada de Fourier se reescribe:
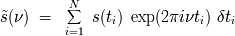
siendo
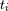
las fechas individuales y
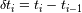
. Si la grabación es lo suficiente regular:
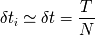
Los tiempos
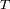
y
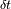
definen las principales propiedades del análisis de Fourier.
Resolución en frecuencia
Una señal observada durante un tiempo total
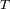
permite una resolución en frecuencia
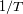
.
Frecuencia de corte
Una señal observada con un paso de muestreo
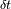
permite seguir las frecuencias hasta el corte a
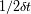
. El factor 2 proviene de la necesidad de observar en 2 medidas distintas una mitad de periodo
negativa y una positiva.
Digitalización
La observación de fenómenos variables debe permitir:
- un muestreo lo suficientemente rápido de la serie temporal como para acceder a las
variaciones las más rápidas
- una duración de observación lo suficientemente larga como para seguir un periodo entero
de un fenómeno periódico
Acordarse
Si grabamos una serie temporal de
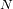
señales, en un tiempo total
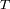
con un paso de digitalización
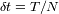
, podemos distinguir sin ambigüedad
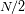
frecuencias, entre
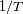
et
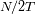
.

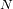 señales, durante un tiempo
señales, durante un tiempo
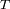 , el análisis por transformada de Fourier se reescribe:
, el análisis por transformada de Fourier se reescribe:
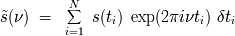
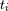 las fechas individuales y
las fechas individuales y
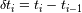 . Si la grabación es lo suficiente regular:
. Si la grabación es lo suficiente regular:
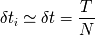
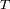 y
y
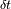 definen las principales propiedades del análisis de Fourier.
definen las principales propiedades del análisis de Fourier.
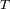 permite una resolución en frecuencia
permite una resolución en frecuencia
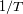 .
.
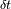 permite seguir las frecuencias hasta el corte a
permite seguir las frecuencias hasta el corte a
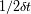 . El factor 2 proviene de la necesidad de observar en 2 medidas distintas una mitad de periodo
negativa y una positiva.
. El factor 2 proviene de la necesidad de observar en 2 medidas distintas una mitad de periodo
negativa y una positiva.
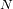 señales, en un tiempo total
señales, en un tiempo total
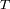 con un paso de digitalización
con un paso de digitalización
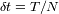 , podemos distinguir sin ambigüedad
, podemos distinguir sin ambigüedad
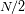 frecuencias, entre
frecuencias, entre
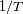 et
et
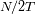 .
.