 Requisitos previos
Requisitos previos
Vista matemática de la transformada de Fourier.
 Objetivos
Objetivos
Presentación de la transformada de Fourier y repaso de algunas propiedades.
Formalismo de la transformación de Fourier
La transformación de Fourier asocia a una función
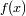
su transformada:
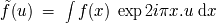
Las variables

y

son conjugadas. A la variable temporal

se le asocia la variable frecuencial

, y a la variable espacial

se le asocia la frecuencia espacial

.
Propiedades
La transformación de Fourier (TF) tiene muchas propiedades (linearidad...). Para más
información, consultar un libro de matemáticas.
La operación inversa de la TF se denota:
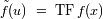
et
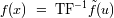
.
Teorema de Parseval-Plancherel
Análisis de Fourier discreto
Se tiene que cambiar un poco la definición de la transformación (continua) para aplicarla a
las señales reales, que son discretas. El análisis de Fourier discreto utiliza una cantidad finita
de capturas de la señal y proporciona una cantidad finita de frecuencias para describirla.
La discretización se realiza sin problemas, porque la TF de una función peine (sucesión de
distribuciones de Dirac a intervalos regulares) es otra función peine. Y la función peine describe
la operación de digitalización.
Análisis de Fourier rápido

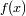 su transformada:
su transformada:
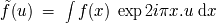
 y
y
 son conjugadas. A la variable temporal
son conjugadas. A la variable temporal
 se le asocia la variable frecuencial
se le asocia la variable frecuencial
 , y a la variable espacial
, y a la variable espacial
 se le asocia la frecuencia espacial
se le asocia la frecuencia espacial
 .
.
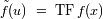 et
et
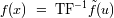 .
.
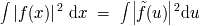


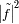
![2 [XY]](../../../../images/tratar/images-TeX4ht/tratar25x.png)
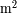 )
) 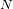 , donde
, donde
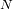 es una potencia de 2 (
es una potencia de 2 (
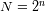 puntos). En caso contrario, no hay ganancia de tiempo. La FFT puede hacerse muy lenta
si la cantidad de punto es un numero primo o se factoriza con grandes factores primos.
puntos). En caso contrario, no hay ganancia de tiempo. La FFT puede hacerse muy lenta
si la cantidad de punto es un numero primo o se factoriza con grandes factores primos.
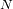 valores conduce a un espectro de
valores conduce a un espectro de
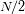 frecuencias.
frecuencias.