 Requisitos previos
Requisitos previos
Aunque recordaremos las bases teóricas, esta lección supone que la red ya ha sido estudiada en clase de física.
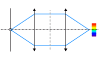
Una red es alimentada con un haz paralelo de una
ranura
y produce una serie de imágenes coloreadas.
 Objetivos
Objetivos
Caracterizar las interferencias constructivas de una red. Estudiar la distribución de energía en la figura de
interferencia.

Interferencias constructivas
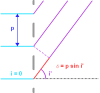
Se denota

al
periodo de la red ,
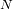
a la cantidad de rayos que la compone y

a la longitud de onda estudiada. La condición para conseguir
interferencias constructivas se
escribe:
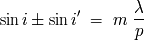
donde

es el orden de interferencia. El signo

en esta relación corresponde a una red por
transmisión. El signo

a una red por
reflexión. Utilizaremos este segundo caso, porque corresponde al de la
red inclinada
.
Esta condición ilustra el hecho que el
desfase

entre las amplitudes complejas que provienen de dos rayos consecutivos vale
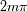
(o que la diferencia de camino vale
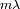
, lo cual es equivalente).

El papel de la difracción y de las interferencias
La
difracción por una ranura de la red
determina las diferentes direcciones hacia las cuales la luz es enviada, dado que cada ranura de la red se
comporta como una fuente secundaria.
Las interferencias entre estas fuentes secundarias construyen franjas de interferencia, que serán más
finas cuantos más rayos tenga la red (consultar el
cálculo
de la intensidad de la figura de interferencia).
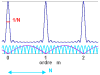
Intensidad de la figura de interferencia
La intensidad de la figura de interferencia proviene del efecto combinado de la difracción por
una sola ranura y de las interferencias por
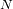
ranuras. Nos interesamos primero en el fenómeno de interferencia por sí solo. Se denota

al desfase entre 2 ranuras consecutivas, y
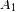
a la amplitud compleja. Haremos los cálculos en la aproximación de Fraunhofer, para demostrar
que la intensidad difractada vale:
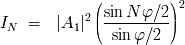
 Demostración
Demostración
La
suma
de las amplitudes conduce a :
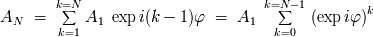
El tratamiento de la suma de los términos de una serie en progresión geométrica
da:
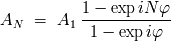
Calculamos la intensidad factorizando el numerador y el denominador mediante la
exponencial compleja del ángulo medio (de módulo unidad) para obtener:
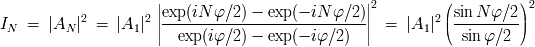
El termino de intensidad es importante sólo cuando el denominador se anula. En este caso, el
numerador se anula también y, por continuidad del cociente, el pico de intensidad tiende
hacia
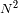
. Cada
pico
corresponde a un orden de interferencia. El tamaño de este pico viene dado por la variación del
numerador que oscila
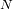
veces más rápido que el denominador. Es entonces
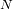
veces inferior al tamaño entre dos órdenes consecutivos.
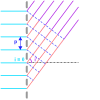
Ineficacia de la red por transmisión
El inconveniente de la red por transmisión es su falta de eficacia. El esencial de la energía pasa en el
orden 0, lo que no es interesante para la dispersión. Otro concepto tecnológico permite conseguir una
buena eficacia: la
red inclinida.

 al periodo de la red ,
al periodo de la red ,
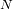 a la cantidad de rayos que la compone y
a la cantidad de rayos que la compone y
 a la longitud de onda estudiada. La condición para conseguir interferencias constructivas se
escribe:
a la longitud de onda estudiada. La condición para conseguir interferencias constructivas se
escribe:
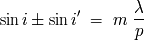
 es el orden de interferencia. El signo
es el orden de interferencia. El signo
 en esta relación corresponde a una red por transmisión. El signo
en esta relación corresponde a una red por transmisión. El signo
 a una red por reflexión. Utilizaremos este segundo caso, porque corresponde al de la red inclinada
.
a una red por reflexión. Utilizaremos este segundo caso, porque corresponde al de la red inclinada
.
 entre las amplitudes complejas que provienen de dos rayos consecutivos vale
entre las amplitudes complejas que provienen de dos rayos consecutivos vale
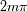 (o que la diferencia de camino vale
(o que la diferencia de camino vale
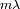 , lo cual es equivalente).
, lo cual es equivalente).
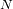 ranuras. Nos interesamos primero en el fenómeno de interferencia por sí solo. Se denota
ranuras. Nos interesamos primero en el fenómeno de interferencia por sí solo. Se denota
 al desfase entre 2 ranuras consecutivas, y
al desfase entre 2 ranuras consecutivas, y
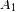 a la amplitud compleja. Haremos los cálculos en la aproximación de Fraunhofer, para demostrar
que la intensidad difractada vale:
a la amplitud compleja. Haremos los cálculos en la aproximación de Fraunhofer, para demostrar
que la intensidad difractada vale:
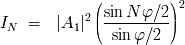
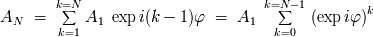
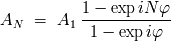
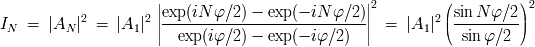
 . Cada pico
corresponde a un orden de interferencia. El tamaño de este pico viene dado por la variación del
numerador que oscila
. Cada pico
corresponde a un orden de interferencia. El tamaño de este pico viene dado por la variación del
numerador que oscila
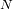 veces más rápido que el denominador. Es entonces
veces más rápido que el denominador. Es entonces
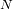 veces inferior al tamaño entre dos órdenes consecutivos.
veces inferior al tamaño entre dos órdenes consecutivos.