 Requisitos previos
Requisitos previos
Lección sobre la difracción de Fraunhofer.
 Objetivos
Objetivos
(Consultar esta lección únicamente en una segunda lectura) Relacionar el formalismo describiendo
la difracción en el infinito por una pupila y el formalismo de la transformación de Fourier.
Difracción y transformada de Fourier
Marcamos un punto de la pupila por la variable

siendo
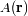
la función que caracteriza la iluminación de la pupila. Entonces, la amplitud difractada en
una dirección angular de vector director

se escribe:
![integral integral [ ] r- dr-- A(u) = pupille A(r) exp - 2ipu. 2 [ c ] c integral integral r- dr-- = P (r) I (r) exp - 2ipu. 2 c c](../../../../images/optica/images-TeX4ht/optica394x.png)
Con el término
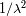
introducido para normalizar el elemento de superficie
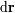
, y siendo
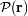
la pupila de entrada que limita la fracción de la onda plana emitida por la fuente en el infinito. Para
una iluminación uniforme en incidencia normal,
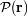
es típicamente una función rectángulo de dos dimensiones.
El formalismo de la transformación de Fourier se escribe
![integral integral f~(u) = f (r) exp [- 2ipu.r] dr](../../../../images/optica/images-TeX4ht/optica399x.png)
El aspecto similar de estas 2 últimas igualdades no es casual.
La TF de la pupila
Si suponemos la iluminación uniforme, la amplitud difractada en una dirección

viene dada por la transformada de Fourier de la función de pupila
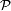
(la variable de posición está normalizada en unidades de longitud de onda):
![integral integral [ r] dr A(u) = A P (r) exp - 2ipu. -- ---- 0 c c2](../../../../images/optica/images-TeX4ht/optica402x.png)
Las variables conjugadas son la dirección angular dada por el vector

, y
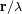
la variable espacial que describe la pupila con dividida por la longitud de onda.
Difracción y filtro
Podemos utilizar las propiedades de la transformada de Fourier para reescribir las
características de la difracción. Una pupila de tamaño

filtra las frecuencias elevadas. Es decir la información angular más fina que
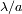
.
Cuanto más grande es la pupila menos filtra angularmente.

 siendo
siendo
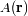 la función que caracteriza la iluminación de la pupila. Entonces, la amplitud difractada en
una dirección angular de vector director
la función que caracteriza la iluminación de la pupila. Entonces, la amplitud difractada en
una dirección angular de vector director
 se escribe:
se escribe:
![integral integral [ ] r- dr-- A(u) = pupille A(r) exp - 2ipu. 2 [ c ] c integral integral r- dr-- = P (r) I (r) exp - 2ipu. 2 c c](../../../../images/optica/images-TeX4ht/optica394x.png)
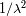 introducido para normalizar el elemento de superficie
introducido para normalizar el elemento de superficie
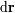 , y siendo
, y siendo
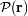 la pupila de entrada que limita la fracción de la onda plana emitida por la fuente en el infinito. Para
una iluminación uniforme en incidencia normal,
la pupila de entrada que limita la fracción de la onda plana emitida por la fuente en el infinito. Para
una iluminación uniforme en incidencia normal,
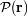 es típicamente una función rectángulo de dos dimensiones.
es típicamente una función rectángulo de dos dimensiones.
![integral integral f~(u) = f (r) exp [- 2ipu.r] dr](../../../../images/optica/images-TeX4ht/optica399x.png)
 viene dada por la transformada de Fourier de la función de pupila
viene dada por la transformada de Fourier de la función de pupila
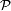 (la variable de posición está normalizada en unidades de longitud de onda):
(la variable de posición está normalizada en unidades de longitud de onda):
![integral integral [ r] dr A(u) = A P (r) exp - 2ipu. -- ---- 0 c c2](../../../../images/optica/images-TeX4ht/optica402x.png)
 , y
, y
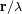 la variable espacial que describe la pupila con dividida por la longitud de onda.
la variable espacial que describe la pupila con dividida por la longitud de onda.
 filtra las frecuencias elevadas. Es decir la información angular más fina que
filtra las frecuencias elevadas. Es decir la información angular más fina que
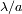 .
.