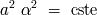Requisitos previos
Requisitos previos
Noción de ángulo solido.
 Objetivos
Objetivos
Definir la extensión del haz, y sobre todo demostrar la conservación de la extensión del haz.
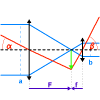
Ejemplo : montaje afocal
Un montaje afocal transforma un haz plano en otro. La razón de los diámetros de estos haces
y de las inclinaciones de entrada y salida dependen del aumento.
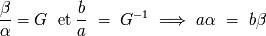
Este producto es un invariante que traduce una relación física más general: la conservación
de la energía del haz.

Haz, extensión del haz y conservación de la energía
La potencia (o
luminosidad
)
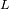
transportada por un haz luminoso, emitida por un elemento de superficie S y recibida por S' se
conserva. Esta potencia es proporcional a la
luminosidad
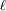
, al elemento de superficie emisor y al elemento de ángulo solido de emisión.
Escribiendo las magnitudes fotométricas de los datos de la
figura,
se puede expresar la conservación de la potencia luminosa como la conservación de la extensión
geométrica del haz. Se define la
extensión del haz como el producto
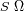
, y se conserva a lo largo del haz. Donde
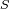
es la sección del elemento óptico atravesado por el haz (colimado: sin perdida de energía),
y
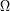
su ángulo solido. Se considera que el medio tiene un índice de 1 (como el vacío o el
aire).
Para los sistemás sin astigmatismo (es decir con aberraciones limitadas), la conservación de la energía se
traduce en la conservación de la extensión del haz:
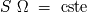
 Demostración
Demostración
Pasar de la luminosidad
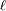
a la potencia luminosa requiere utilizar el producto de un elemento de superficie emisor
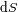
y un ángulo solido de emisión
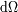
. La luminosidad elemental se escribe:
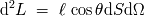
El ángulo solido "ve'' una superficie receptora
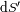
a la distancia

definida como:
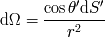
La luminosidad elemental se escribe entonces:
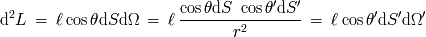
Con
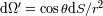
el ángulo solido de la fuente vista desde la superficie receptora. Podemos ver que los
papeles de los elementos emisores y receptores son simétricos. El producto
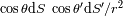
introduce la extensión geométrica elemental.
La integración del haz entero a través de una pupila (realizado en el espacio objeto o
imagen) guarda la simetría del producto superficie por ángulo solido:
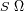
.
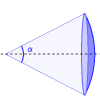
Haz cónico poco abierto
Un haz cónico de apertura total

cubre un ángulo solido:
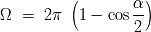
Si el ángulo

es pequeño, este ángulo solido se escribe simplemente:
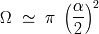
A través una óptica de diámetro

, la conservación del producto
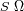
se vuelve (para un haz cónico):
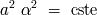
Encontramos otra vez el resultado conseguido en el caso del montaje afocal.
Algunas consecuencias
Podemos notar las consecuencias importantes siguientes:
- cuanto más fino sea el diámetro por el que pasa el haz colectado, más divergente será éste,
- cuanto mayor sea la superficie del colector mayor será la extensión del haz. En ese caso,
mayores tienen que ser los instrumentos para recibir un haz de gran diámetro,
- la superficie del detector y el ángulo que puede ver (del orden del ángulo de apertura del
telescopio) limitan el tamaño angular del campo objeto.
Extensión de haz coherente
Un haz monocromático es
coherente
sobre una extensión igual a
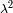
(ver la justificación dada en el
ejercicio
).

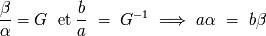
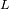 transportada por un haz luminoso, emitida por un elemento de superficie S y recibida por S' se
conserva. Esta potencia es proporcional a la luminosidad
transportada por un haz luminoso, emitida por un elemento de superficie S y recibida por S' se
conserva. Esta potencia es proporcional a la luminosidad
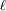 , al elemento de superficie emisor y al elemento de ángulo solido de emisión.
, al elemento de superficie emisor y al elemento de ángulo solido de emisión.
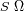 , y se conserva a lo largo del haz. Donde
, y se conserva a lo largo del haz. Donde
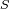 es la sección del elemento óptico atravesado por el haz (colimado: sin perdida de energía),
y
es la sección del elemento óptico atravesado por el haz (colimado: sin perdida de energía),
y
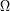 su ángulo solido. Se considera que el medio tiene un índice de 1 (como el vacío o el
aire).
su ángulo solido. Se considera que el medio tiene un índice de 1 (como el vacío o el
aire).
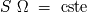
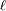 a la potencia luminosa requiere utilizar el producto de un elemento de superficie emisor
a la potencia luminosa requiere utilizar el producto de un elemento de superficie emisor
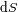 y un ángulo solido de emisión
y un ángulo solido de emisión
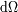 . La luminosidad elemental se escribe:
. La luminosidad elemental se escribe:
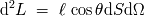
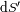 a la distancia
a la distancia
 definida como:
definida como:
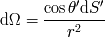
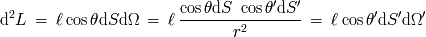
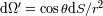 el ángulo solido de la fuente vista desde la superficie receptora. Podemos ver que los
papeles de los elementos emisores y receptores son simétricos. El producto
el ángulo solido de la fuente vista desde la superficie receptora. Podemos ver que los
papeles de los elementos emisores y receptores son simétricos. El producto
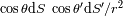 introduce la extensión geométrica elemental.
introduce la extensión geométrica elemental.
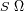 .
.
 cubre un ángulo solido:
cubre un ángulo solido:
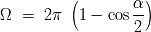
 es pequeño, este ángulo solido se escribe simplemente:
es pequeño, este ángulo solido se escribe simplemente:
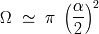
 , la conservación del producto
, la conservación del producto
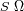 se vuelve (para un haz cónico):
se vuelve (para un haz cónico):