 Requisitos previos
Requisitos previos
Difracción de Fraunhofer.
 Objetivos
Objetivos
(Una segunda lectura) Introducir las funciones de Bessel para una apertura circular. Éstas justifican el
factor
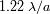
que dimensiona la difracción.
Difracción por cualquier pupila
Consideramos una pupila modelizado por una apertura plana centrada en
. Sea
un punto de la pupila. Esta pupila está iluminada por una onda uniforme, monocromática, en
incidencia normal. La amplitud de la onda difractada en la dirección del vector director

se escribe
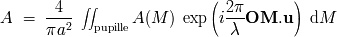
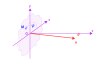
Pupila circular
La pupila es circular, de radio
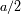
. De este modo es más simple escribir las coordenadas del punto
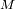
y de la dirección de difracción

en coordenadas polares, con la notación siguiente:
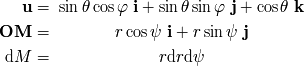
(
es el vector normal al plano de la pupila). La amplitud de la onda difractada en la
dirección

forma un ángulo

con el eje óptico. Se escribe entonces (suponiendo la amplitud incidente uniforme):
Se introducen ahora las funciones de Bessel. Los dos primeros términos son
por definición :
![1 integral J (X ) = ---- 2p exp[ - iX cos v] dv 0 2p 0 integral -1- X J1(X ) = 0 uJ0(u) du X](../../../../images/optica/images-TeX4ht/optica377x.png)
La amplitud difractada en una dirección haciendo un pequeño ángulo

con el eje óptico se escribe entonces:
 Demostración
Demostración
Los cálculos pasan por cambios de variable
La intensidad difractada en la dirección

se escribe entonces:
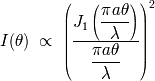
Ceros, anillos y tamaño a media altura
Para valores de
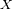
cercanos a 0,
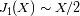
. Por otra parte, el primer cero de la función
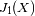
ocurre para
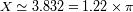
.
El tamaño a media altura del pico central de difracción (que se supone igual a la mitad de la
distancia entre los 2 ceros de cada lado del pico central) se escribe en función del diámetro de
la pupila

y del tamaño de onda

:
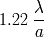
La figura de difracción se anula después para los radios 2.23, 3.23, 4.24, 5.24.... en unidades
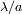
. Los anillos luminosos tienen como radios: 1.63, 2.68, 3.70, 4.71, 5.71... en las mismas unidades.

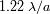 que dimensiona la difracción.
que dimensiona la difracción. 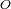 . Sea
. Sea
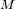 un punto de la pupila. Esta pupila está iluminada por una onda uniforme, monocromática, en
incidencia normal. La amplitud de la onda difractada en la dirección del vector director
un punto de la pupila. Esta pupila está iluminada por una onda uniforme, monocromática, en
incidencia normal. La amplitud de la onda difractada en la dirección del vector director
 se escribe
se escribe
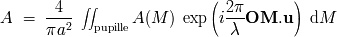
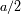 . De este modo es más simple escribir las coordenadas del punto
. De este modo es más simple escribir las coordenadas del punto
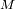 y de la dirección de difracción
y de la dirección de difracción
 en coordenadas polares, con la notación siguiente:
en coordenadas polares, con la notación siguiente:
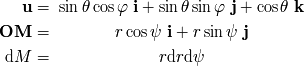
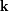 es el vector normal al plano de la pupila). La amplitud de la onda difractada en la
dirección
es el vector normal al plano de la pupila). La amplitud de la onda difractada en la
dirección
 forma un ángulo
forma un ángulo
 con el eje óptico. Se escribe entonces (suponiendo la amplitud incidente uniforme):
con el eje óptico. Se escribe entonces (suponiendo la amplitud incidente uniforme):
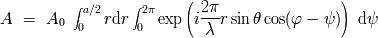
![1 integral J (X ) = ---- 2p exp[ - iX cos v] dv 0 2p 0 integral -1- X J1(X ) = 0 uJ0(u) du X](../../../../images/optica/images-TeX4ht/optica377x.png)
 con el eje óptico se escribe entonces:
con el eje óptico se escribe entonces:
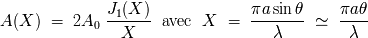
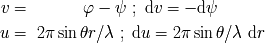
 se escribe entonces:
se escribe entonces:
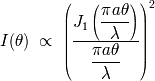
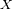 cercanos a 0,
cercanos a 0,
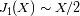 . Por otra parte, el primer cero de la función
. Por otra parte, el primer cero de la función
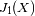 ocurre para
ocurre para
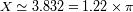 .
El tamaño a media altura del pico central de difracción (que se supone igual a la mitad de la
distancia entre los 2 ceros de cada lado del pico central) se escribe en función del diámetro de
la pupila
.
El tamaño a media altura del pico central de difracción (que se supone igual a la mitad de la
distancia entre los 2 ceros de cada lado del pico central) se escribe en función del diámetro de
la pupila
 y del tamaño de onda
y del tamaño de onda
 :
:
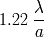
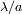 . Los anillos luminosos tienen como radios: 1.63, 2.68, 3.70, 4.71, 5.71... en las mismas unidades.
. Los anillos luminosos tienen como radios: 1.63, 2.68, 3.70, 4.71, 5.71... en las mismas unidades.