Caso circular
La situación más simple es aquélla en la que
la órbita es circular y vista de lado, es decir con
una inclinación de
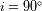
(el plano de la órbita contiene la línea de mira). En ese caso las dos curvas de velocidad radial
son sinusoides que oscilan en fase, alrededor de la velocidad
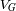
de su baricentro, con el mismo periodo
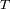
.
Como cada una de las estrellas A y B están dotadas de un movimiento circular y uniforme de
periodo
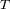
alrededor de G, las velocidades
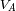
y
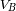
están ligadas a las distancias
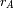
y

según las relaciones:
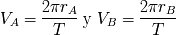
Masas
Por definición del centro de masas :
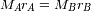
. A partir de ello hallamos la razón entre las masas
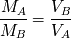
que viene dada en función de la razón de las amplitudes de las dos curvas. Por otro lado, según la
tercera ley de Kepler,
tenemos que
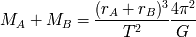
Obtenemos:
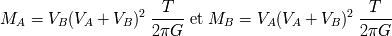
Si la inclinación

es diferente de
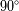
, la amplitud de la curva de velocidad radial disminuye en un factor
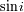
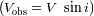
.
En ese caso en las ecuaciones precedentes,
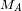
es remplazado por
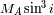
(respectivamente
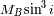
).
Órbita elíptica
Si la órbita no es circular sino elíptica con una excentricidad

no nula, las curvas de velocidad radial ya no son sinusoidales, aunque sigan en oposición de
fase y con una razón de amplitudes igual a la razón de masas.

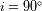 (el plano de la órbita contiene la línea de mira). En ese caso las dos curvas de velocidad radial
son sinusoides que oscilan en fase, alrededor de la velocidad
(el plano de la órbita contiene la línea de mira). En ese caso las dos curvas de velocidad radial
son sinusoides que oscilan en fase, alrededor de la velocidad
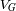 de su baricentro, con el mismo periodo
de su baricentro, con el mismo periodo
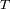 .
.
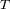 alrededor de G, las velocidades
alrededor de G, las velocidades
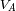 y
y
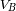 están ligadas a las distancias
están ligadas a las distancias
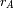 y
y
 según las relaciones:
según las relaciones:
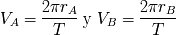
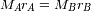 . A partir de ello hallamos la razón entre las masas
. A partir de ello hallamos la razón entre las masas
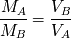
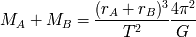
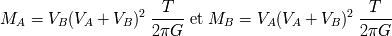
 es diferente de
es diferente de
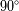 , la amplitud de la curva de velocidad radial disminuye en un factor
, la amplitud de la curva de velocidad radial disminuye en un factor
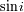
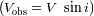 .
.
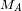 es remplazado por
es remplazado por
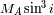 (respectivamente
(respectivamente
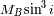 ).
).
 no nula, las curvas de velocidad radial ya no son sinusoidales, aunque sigan en oposición de
fase y con una razón de amplitudes igual a la razón de masas.
no nula, las curvas de velocidad radial ya no son sinusoidales, aunque sigan en oposición de
fase y con una razón de amplitudes igual a la razón de masas.