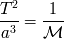Objetivos
Objetivos
La tercera ley de Kepler tiene en sí misma, como cualquier ley física, una potencialidad enorme : generalizar lo
particular, para comprender mejor cómo funciona el Universo.
Ocurre que desde este punto de vista, funciona extraordinariamente bien. Permite "pesar" cualquier objeto del
Universo, con la única condición de que haya un objeto menos masivo que gire alrededor de
él.
Determinar la masa del centro de fuerzas
No hay que interpretar el término pesar en este tema desde un punto de vista físico (medir el
peso) sino desde el punto de vista de la vida corriente : medir la masa.
La mecánica newtoniana permite precisar la constante que interviene en la tercera ley de Kepler
aplicada a un sistema parecido al sistema solar : uno o varios objetos poco masivos que giran
en el potencial central de un cuerpo más masivo.
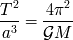
Esta ley implica tres parámetros físicos : El periodo
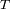
de revolución, el semieje mayor de la órbita y la masa
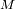
del cuerpo central.
La medida de dos de estos tres parámetros permite deducir el tercero : esto es aprovechado
para determinar la masa
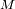
del centro de fuerzas a partir de los parámetros orbitales

y
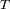
. Estos dos términos son, en efecto, observables, mientras que la masa no lo es.
La medida del periodo
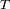
necesita localizar el movimiento a lo largo de la trayectoria.
La medida del semieje mayor de la órbita deriva de la medida de su tamaño angular, y precisa
conocer la distancia del sistema. Se ve una vez más la importancia de la
medida de
distancias
en astronomía.


Diferentes sistemas de unidades
Si se elige un sistema de unidades donde los tiempos se cuentan en años, las distancias en unidades
astronómicas y las masas en masas solares, la
tercera ley de Kepler
se reescribe para el sistema solar, como
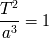
Sin llevar a cabo
ningún cálculo,
el caso de la órbita terrestre, para el cual

= 1 UA,
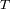
= 1 año, basta para verificar la corrección de las unidades, lo que valida el caso de cualquier otro
planeta.
Para otro sistema caracterizado por un centro de fuerzas de masa
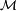
, la tercera ley se transforma, siempre en el sistema de unidades (UA, año,
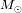
) :
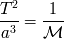
Una aplicación de esta ley en
distintos ejemplos
ilustra cómo una ley física puede extender su validez a una amplia gama de valores.

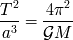
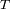 de revolución, el semieje mayor de la órbita y la masa
de revolución, el semieje mayor de la órbita y la masa
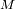 del cuerpo central.
del cuerpo central.
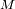 del centro de fuerzas a partir de los parámetros orbitales
del centro de fuerzas a partir de los parámetros orbitales
 y
y
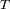 . Estos dos términos son, en efecto, observables, mientras que la masa no lo es.
. Estos dos términos son, en efecto, observables, mientras que la masa no lo es.
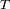 necesita localizar el movimiento a lo largo de la trayectoria.
necesita localizar el movimiento a lo largo de la trayectoria.
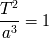
 = 1 UA,
= 1 UA,
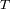 = 1 año, basta para verificar la corrección de las unidades, lo que valida el caso de cualquier otro
planeta.
= 1 año, basta para verificar la corrección de las unidades, lo que valida el caso de cualquier otro
planeta.
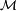 , la tercera ley se transforma, siempre en el sistema de unidades (UA, año,
, la tercera ley se transforma, siempre en el sistema de unidades (UA, año,
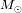 ) :
) :