Hipótesis
El estudio de las masas de los principales objetos del sistema solar desvela un peso pesado,
el Sol, rodeado por un cortejo de pequeños objetos, los planetas. Este hecho determina las
aproximaciones hechas habitualmente para describir el movimiento de un planeta : se considera
que su masa es despreciable con respecto a la masa del Sol, y se desprecian las interacciones
interplanetarias.
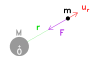
El problema de dos cuerpos
El problema se resume en la inteacción entre dos cuerpos, el Sol de masa
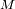
y el planeta de masa
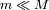
. El referencial de estudio es heliocéntrico, de centro
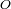
. El planeta
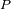
queda localizado por el radiovector
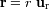
.
El planeta siente una fuerza
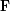
por parte del Sol, expresada por:
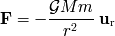
El estudio completo del movimiento es un poco técnico. La resolución por las fórmulas de Binet no será
detallada en este curso ; otro modo de resolución, introduciendo el vector excentricidad, es propuesto en
este
ejercicio
Las leyes de Kepler
La relación fundamental de la dinámica permite deducir que la trayectoria es plana.
Denominamos como
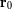
y
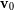
a la posición y velocidad del planeta en un instante dado. Y también como
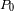
al plano definido por estos dos vectores. La relación dice entonces que la aceleración
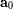
, colinear con
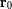
, está igualmente en este plano. Debido a que ningún término de aceleración se dirige fuera del
plano, cualquier trayectoria está necesariamente inscrita en él.
Como basta que la fuerza sea central para que el momento cinético del sistema sea conservado,
la derivación de la segunda ley de Kepler es inmediata.
La tercera ley de Kepler es fácilmente deducida en el caso particular de una trayectoria circular. La
demostración está propuesta en este
ejercicio.

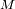 y el planeta de masa
y el planeta de masa
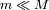 . El referencial de estudio es heliocéntrico, de centro
. El referencial de estudio es heliocéntrico, de centro
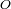 . El planeta
. El planeta
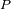 queda localizado por el radiovector
queda localizado por el radiovector
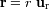 .
El planeta siente una fuerza
.
El planeta siente una fuerza
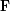 por parte del Sol, expresada por:
por parte del Sol, expresada por:
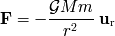
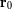 y
y
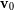 a la posición y velocidad del planeta en un instante dado. Y también como
a la posición y velocidad del planeta en un instante dado. Y también como
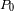 al plano definido por estos dos vectores. La relación dice entonces que la aceleración
al plano definido por estos dos vectores. La relación dice entonces que la aceleración
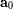 , colinear con
, colinear con
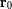 , está igualmente en este plano. Debido a que ningún término de aceleración se dirige fuera del
plano, cualquier trayectoria está necesariamente inscrita en él.
Como basta que la fuerza sea central para que el momento cinético del sistema sea conservado,
la derivación de la segunda ley de Kepler es inmediata.
, está igualmente en este plano. Debido a que ningún término de aceleración se dirige fuera del
plano, cualquier trayectoria está necesariamente inscrita en él.
Como basta que la fuerza sea central para que el momento cinético del sistema sea conservado,
la derivación de la segunda ley de Kepler es inmediata.