Una manera muy elegante de hacer física consite en asociar un
invariante a una
ley física.
El objetivo de este ejercicio es encontrar qué invariante está asociado al hecho de que el módulo
de la fuerza gravitacional varíe como la inversa del cuadrado de la distancia. Ello permite
encontrar la ecuación de la trayectoria elíptica de un satélite en un campo de fuerzas central,
aún requiriendo algunos cálculos.
Consideremos un satélite, de masa

, en el campo de fuerzas central de un cuerpo de masa
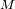
. Localizamos su posición por el vector radial
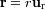
. Denotamos
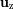
al vector ortonormal perpendicular al plano de la trayectoria, que determina el momento
cinético del satélite, de tal manera que el triedro
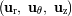
forme un triedro ortonormal directo.
4)
Multiplicamos escalarmente la ecuación obtenida anteriormente por el vector posición

. Demostrar que esto permite encontrar la ecuación de la trayectoria
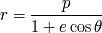
eligiendo como origen de la variable angular

la dirección y el sentido del vector excentricidad
 ayuda
solución
ayuda
solución

 , en el campo de fuerzas central de un cuerpo de masa
, en el campo de fuerzas central de un cuerpo de masa
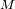 . Localizamos su posición por el vector radial
. Localizamos su posición por el vector radial
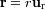 . Denotamos
. Denotamos
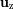 al vector ortonormal perpendicular al plano de la trayectoria, que determina el momento
cinético del satélite, de tal manera que el triedro
al vector ortonormal perpendicular al plano de la trayectoria, que determina el momento
cinético del satélite, de tal manera que el triedro
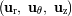 forme un triedro ortonormal directo.
forme un triedro ortonormal directo.