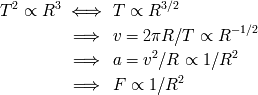Objetivos
Objetivos
La página
"De las leyes de Newton a las leyes de Kepler"
muestra cómo se derivan hoy en día las leyes de Kepler a partir de las leyes de la gravitación y del formalismo de
la mecánica clásica. Pero históricamente, las tres leyes de Kepler son anteriores al formalismo
newtoniano, al igual que frecuentemente el hecho observacional precede a la formalización teórica.
Es importante ver cómo las leyes de Kepler llevan en sí las semillas de la ley de gravitación.
Lo que indujo la primera ley
La
primera ley de Kepler
da un papel particular al Sol, que puede ser interpretado de dos maneras.
Desde un punto de vista dinámico, el papel central del Sol está claramente enunciado. Aunque hoy la
preponderancia del Sol en el seno del sistema solar sea un hecho reconocido, no era así en el siglo XVII.
El Sol es el centro de fuerzas, más aún cuando toda la masa del sistema solar es despreciable con
respecto a su masa.
En términos del referencial de estudio, la primera ley introdujo claramente el referencial heliocéntrico,
que es el "buen" referencial de estudio, puesto que es bastante más galileano que el referencial
geocéntrico. La primera ley identifica claramente un centro de fuerzas supuesto inmóvil, así como el
buen referencial asociado.
Lo que induce la segunda ley
La
segunda ley de Kepler
enuncia la ley de las áreas, es decir, la conservación del momento cinético del sistema. Esto es específico
de las fuerzas centrales. De la primera y segunda leyes nace entonces la idea de que el Sol es el centro de
fuerzas. Esta fuerza puede escribirse como
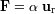
, siendo el vector
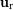
un
vector unitario radial
definido con respecto al centro de fuerzas.
Lo que induce la tercera ley
La relación entre el periodo y el
semieje mayor dada por la
tercera ley de
Kepler
es específica de una dependencia particular del módulo de la fuerza y la variable radial. Esta ley sólo
aparecerá para una fuerza que varíe como
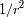
.
El conjunto de las leyes de Kepler conduce finalmente a una fuerza que se puede expresar de la manera
siguiente:
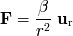
Las leyes de Kepler no dan más información acerca del parámetro
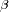
. Son las
leyes de gravitación,
debidas a Isaac Newton, las que permiten obtener su forma explícita.
De las leyes de Kepler a una fuerza central que varía como la inversa del cuadrado de la distancia
 Demostración
Demostración
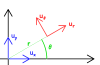
En coordenadas polares planas ,
definidas en el plano de la órbita con respecto al foco descrito por la primera ley de
Kepler, el radiovector, la velocidad y la aceleración del objeto se describen según:
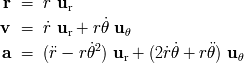
La componente ortoradial de la aceleración se identifica, si eliminamos las constantes, con la
derivada temporal del momento cinético (perpendicular al plano de la trayectoria) :
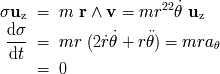
La nulidad de la componente ortoradial de la aceleración se debe a la existencia de una
fuerza
central.
La demostración de la tercera ley de Kepler, en el caso de un movimiento circular, se deriva de
la formulación siguiente, donde
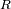
es el radio de la órbita,
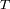
el periodo y

la velocidad del objeto:
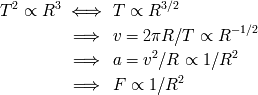

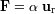 , siendo el vector
, siendo el vector
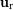 un vector unitario radial
definido con respecto al centro de fuerzas.
un vector unitario radial
definido con respecto al centro de fuerzas.
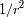 .
.
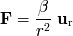
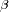 . Son las leyes de gravitación,
debidas a Isaac Newton, las que permiten obtener su forma explícita.
. Son las leyes de gravitación,
debidas a Isaac Newton, las que permiten obtener su forma explícita.
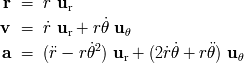
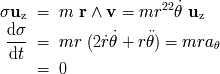
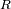 es el radio de la órbita,
es el radio de la órbita,
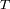 el periodo y
el periodo y
 la velocidad del objeto:
la velocidad del objeto: