Elipses, parábolas e hipérbolas

Las trayectorias que son la solución del problema de dos cuerpos dependen de la energía mecánica total del sistema y de su momento cinético, y pueden ser circulares, elípticas, parabólicas o hiperbólicas.
En coordenadas polares, la trayectoria de un sistema en el contexto del problema de dos cuerpos tiene como ecuación paramétrica:

Esta expresión puede obtenerse a partir de las ecuaciones del movimiento de un sistema de dos cuerpos por el estudio de las ecuaciones de Binet (consultar un curso de física); o por el vector excentricidad.
Dos parámetros bastan para definir la trayectoria en su plano.

• La excentricidad define la naturaleza de la cónica
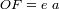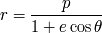
• El parámetro es una magnitud relacionada con el semieje mayor y la excentricidad .

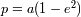• El radiovector está definido con respecto al foco 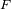de la elipse que define el centro de fuerza, y no con respecto al centro .
• El punto más cercano al foco es el periastro ; el punto más alejado es el apoastro
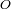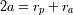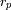• El semieje mayor verifica , con y 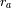los radios del peri y apoastro.
• 
• 
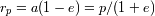
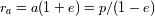
• El parámetro de la elipse verifica
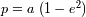
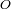• La distancia del centro al foco 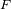vale

• En el sistema solar, cuanto más masivo es un objeto, más tiende su trayectoria a ser circular; los asteroides tienen trayectorias generalmente más elípticas que la mayoría de los planetas.
• Los cometas de gran periodo tienen trayectorias muy elípticas.
• Los cometas de muy gran periodo tienen trayectorias a menudo indeterminadas; de hecho suelen ser muy sensibles a las perturbaciones gravitacionales.