 Objetivos
Objetivos
Encontrar rapidamente las diferentes trayectorias posibles en un potencial gravitacional, analizando el
movimiento radial de una partícula de prueba.
En el siguiente
ejercicio
se calcula explicitamente una trayectoria.
Leyes de conservación
En un potencial gravitacional de masa
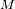
, un objeto de masa

conserva una energía mecánica
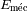
constante, suma de las energías cinética y potencial, igual a:
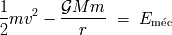
En coordenadas polares, el cuadrado de la velocidad se escribe:
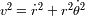
.
De manera que la conservación del momento cinético se enuncia:
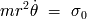
Y la velocidad angular
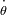
se expresa en funcion del invariante
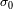
y de la variable radial

según:
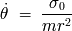

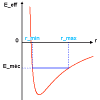
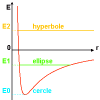
El potencial efectivo
Eliminando la variable angular de la ecuación de conservación de energía, llegamos a una
ecuación que relaciona la energía cinética radial
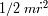
con un potencial únicamente radial :
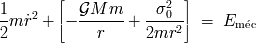
Decidimos entonces estudiar el
movimiento radial del sistema que posee
la energía potencial
efectiva:
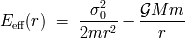
Identificamos la
suma
de dos contribuciones:
- término gravitacional en
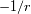
- término rotacional en
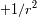
El movimiento radial se estudia con ayuda de la
curva de potencial efectivo.
Las diferentes
excursiones radiales
dependen de la energía
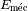
del sistema.

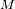 , un objeto de masa
, un objeto de masa
 conserva una energía mecánica
conserva una energía mecánica
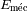 constante, suma de las energías cinética y potencial, igual a:
constante, suma de las energías cinética y potencial, igual a:
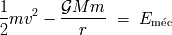
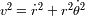 .
.
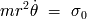
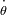 se expresa en funcion del invariante
se expresa en funcion del invariante
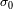 y de la variable radial
y de la variable radial
 según:
según:
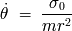
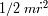 con un potencial únicamente radial :
con un potencial únicamente radial :
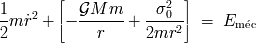
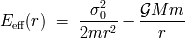
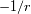
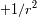
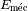 del sistema.
del sistema.