 Objetivos
Objetivos
Reconstituir los elementos geométricos de la órbita verdadera del sistema.
 Requisitos previos
Requisitos previos
Elementos geométricos que definen una trayectoria
elíptica
Semieje mayor
La observación da una serie de posiciones relativas de las dos estrellas en el cielo. Eligiendo la
estrella más brillante (E2) como origen de las coordenadas, las posiciones de la estrella más
débil (E1) se sitúan en una elipse, pero ocurre que E2 no está en el foco de la órbita proyectada.
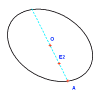
Sea O el centro de la elipse aparente y A la intersección de la recta OE2 con la elipse, en
el punto más cercano a E2; O es la proyección del centro de la órbita verdadera y A es la
proyección de su perigeo. El segmento [OA] es la proyección del semieje mayor de la órbita
verdadera.
Excentricidad
La excentricidad

, relación entre la distancia centro-foco y el semieje mayor, es conservada por proyección e igual
a OE2/OA.
inclinación
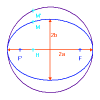
La inlinación

de la órbita verdadera con el plano del cielo se haya reconstituyendo la proyección del círculo
principal de la elipse verdadera: este círculo se proyecta siguiendo una elipse cuya relación de
ejes es igual a

.
Se utiliza para ello una propiedad de la elipse y de su círculo principal: la dirección paralela al
diámetro conjugado del eje mayor pasando por un punto
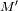
de la elipse corta al círculo principal en un punto
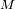
y el eje mayor en un punto
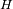
, tales que
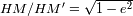
. Dado que esta propiedad se conserva por proyección se puede reconstituir la elipse proyección
del círculo principal punto por punto a partir de la trayectoria observada y de la dirección
conjugada, por ejemplo la dirección de la tangente a la elipse observada en los puntos
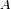
y
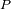
.
El semieje mayor de la órbita verdadera es finalmente igual a
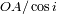
.

 , relación entre la distancia centro-foco y el semieje mayor, es conservada por proyección e igual
a OE2/OA.
, relación entre la distancia centro-foco y el semieje mayor, es conservada por proyección e igual
a OE2/OA.
 de la órbita verdadera con el plano del cielo se haya reconstituyendo la proyección del círculo
principal de la elipse verdadera: este círculo se proyecta siguiendo una elipse cuya relación de
ejes es igual a
de la órbita verdadera con el plano del cielo se haya reconstituyendo la proyección del círculo
principal de la elipse verdadera: este círculo se proyecta siguiendo una elipse cuya relación de
ejes es igual a
 .
.
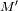 de la elipse corta al círculo principal en un punto
de la elipse corta al círculo principal en un punto
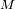 y el eje mayor en un punto
y el eje mayor en un punto
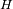 , tales que
, tales que
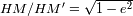 . Dado que esta propiedad se conserva por proyección se puede reconstituir la elipse proyección
del círculo principal punto por punto a partir de la trayectoria observada y de la dirección
conjugada, por ejemplo la dirección de la tangente a la elipse observada en los puntos
. Dado que esta propiedad se conserva por proyección se puede reconstituir la elipse proyección
del círculo principal punto por punto a partir de la trayectoria observada y de la dirección
conjugada, por ejemplo la dirección de la tangente a la elipse observada en los puntos
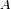 y
y
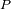 .
.
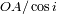 .
.