 Ejercicio 'Esfera de influencia'
Ejercicio 'Esfera de influencia'
Nivel **
Tiempo necesario :
30 min
La esfera de influencia de un planeta de masa

que orbita en una órbita circular de radio

alrededor de una estrella de masa
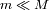
puede ser definida como la zona en el interior de la cual un satélite permanece atrapado
alrededor del planeta (en el exterior de esta esfera, el satélite es capturado en órbita alrededor
de la estrella). Para determinar el radio de esta esfera se busca en el referencial que gira con
el planeta la posición de equilibrio entre los dos cuerpos
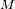
y

. Se denota
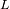
a esta posición (primer punto de Lagrange).
1)
Sea
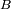
la distancia de
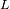
al planeta. Determinar las distancias de
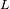
a la estrella y de
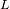
al baricentro
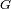
del sistema (planeta-estrella) en función de

y

. Esta última distancia se denota como

.
2)
Demostrar, identificando los diferentes términos, que la relación siguiente define el estado de equilibro
del satélite en el referencial baricéntrico:
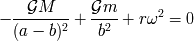
3)
Desarrollar esta relación utilizando únicamente los términos de orden 0 ó 1 (
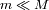
y
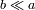
). Deducir a partir de ello que:
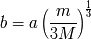
4)
Aplicación numérica:
Calcular

para la Tierra (
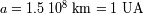
) y comparar la distancia Tierra-Luna (380 000 km). Calcular

para el Sol que orbita alrededor del centro galáctico (
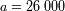
años luz, masa
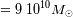
), y comparar con la distancia media entre dos estrellas (distancia Sol-Próxima del Centauro = 4.2 AL)
al igual que la distancia de la nube de Oort (del orden de
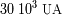
).

 que orbita en una órbita circular de radio
que orbita en una órbita circular de radio
 alrededor de una estrella de masa
alrededor de una estrella de masa
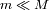 puede ser definida como la zona en el interior de la cual un satélite permanece atrapado
alrededor del planeta (en el exterior de esta esfera, el satélite es capturado en órbita alrededor
de la estrella). Para determinar el radio de esta esfera se busca en el referencial que gira con
el planeta la posición de equilibrio entre los dos cuerpos
puede ser definida como la zona en el interior de la cual un satélite permanece atrapado
alrededor del planeta (en el exterior de esta esfera, el satélite es capturado en órbita alrededor
de la estrella). Para determinar el radio de esta esfera se busca en el referencial que gira con
el planeta la posición de equilibrio entre los dos cuerpos
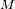 y
y
 . Se denota
. Se denota
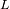 a esta posición (primer punto de Lagrange).
a esta posición (primer punto de Lagrange).
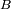 la distancia de
la distancia de
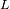 al planeta. Determinar las distancias de
al planeta. Determinar las distancias de
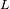 a la estrella y de
a la estrella y de
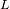 al baricentro
al baricentro
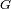 del sistema (planeta-estrella) en función de
del sistema (planeta-estrella) en función de
 y
y
 . Esta última distancia se denota como
. Esta última distancia se denota como
 .
.
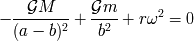
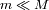 y
y
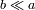 ). Deducir a partir de ello que:
). Deducir a partir de ello que:
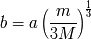
 para la Tierra (
para la Tierra (
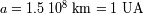 ) y comparar la distancia Tierra-Luna (380 000 km). Calcular
) y comparar la distancia Tierra-Luna (380 000 km). Calcular
 para el Sol que orbita alrededor del centro galáctico (
para el Sol que orbita alrededor del centro galáctico (
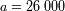 años luz, masa
años luz, masa
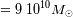 ), y comparar con la distancia media entre dos estrellas (distancia Sol-Próxima del Centauro = 4.2 AL)
al igual que la distancia de la nube de Oort (del orden de
), y comparar con la distancia media entre dos estrellas (distancia Sol-Próxima del Centauro = 4.2 AL)
al igual que la distancia de la nube de Oort (del orden de
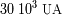 ).
).