La Tierra no es un punto, sino que tiene unas dimensiones finitas. Es decir la intensidad del
campo gravitacional de la Luna varía con la inversa del cuadrado de la distancia a la misma.
La consecuencia de ello es una atracción diferencial que deforma la Tierra. Se puede estimar
el valor del campo de marea
en el contexto del modelo de océano global. Se demuestra que el módulo de
 Demostración
Demostración
Cálculo del campo de marea.
Se estima la marea creada por la Luna
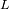
en un punto
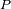
del globo terrestre cuyas coordenadas son dadas en función al centro
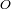
de la Tierra.
Se denota
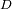
a la distancia
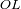
y
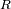
al radio terrestre. La componente del campo de marea
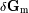
en
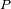
representa la diferencia de campo lunar entre los puntos
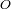
y
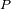
. Los cálculos se reducen a primer orden con respecto al término
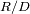
(puesto que
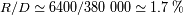
) :
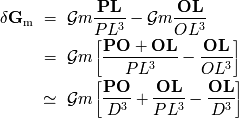
Se estima entonces el término
de la ecuación precedente, introduciendo la relación de Chasles
, y aplicando el primer orden en
:
![OL---- ---OL------- ---------OL------------ 3 = 2 3/2 = 2 3/2 P L [PL ] [(PO + OL) ] OL -~ ----------------------------------- D3 (1 + 2 PO.OL/D2)3/2 OL ( 2) -~ ------ 1 - 3 PO.OL/D D3](../../../../images/marea/images-TeX4ht/marea39x.png)
Se encuentra entonces para el campo de marea
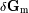
introduciendo los vectores unitarios

y

de tal manera que
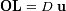
y
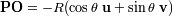
:
![|_ PO 3 PO.OL OL _| dG = Gm |_ ------- -------------- ----- _| m D3 D2 D3 Gm--- = 3 [- R (cos h u + sin h v) + 3R cos h u] D GmR = --------[2 cos h u - sin h v] D3](../../../../images/marea/images-TeX4ht/marea45x.png)
Se pueden comparar los módulos de los campos de marea y gravitacional:
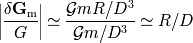
A partir de este análisis se puede deducir que el efecto de marea:

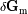 en el contexto del modelo de océano global. Se demuestra que el módulo de
en el contexto del modelo de océano global. Se demuestra que el módulo de
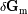 es del orden de
es del orden de
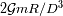
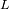 en un punto
en un punto
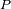 del globo terrestre cuyas coordenadas son dadas en función al centro
del globo terrestre cuyas coordenadas son dadas en función al centro
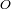 de la Tierra.
Se denota
de la Tierra.
Se denota
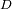 a la distancia
a la distancia
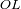 y
y
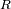 al radio terrestre. La componente del campo de marea
al radio terrestre. La componente del campo de marea
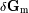 en
en
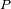 representa la diferencia de campo lunar entre los puntos
representa la diferencia de campo lunar entre los puntos
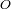 y
y
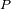 . Los cálculos se reducen a primer orden con respecto al término
. Los cálculos se reducen a primer orden con respecto al término
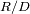 (puesto que
(puesto que
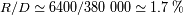 ) :
) :
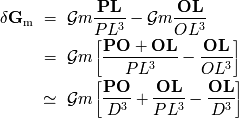
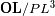 de la ecuación precedente, introduciendo la relación de Chasles
de la ecuación precedente, introduciendo la relación de Chasles
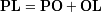 , y aplicando el primer orden en
, y aplicando el primer orden en
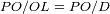 :
:
![OL---- ---OL------- ---------OL------------ 3 = 2 3/2 = 2 3/2 P L [PL ] [(PO + OL) ] OL -~ ----------------------------------- D3 (1 + 2 PO.OL/D2)3/2 OL ( 2) -~ ------ 1 - 3 PO.OL/D D3](../../../../images/marea/images-TeX4ht/marea39x.png)
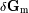 introduciendo los vectores unitarios
introduciendo los vectores unitarios
 y
y
 de tal manera que
de tal manera que
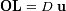 y
y
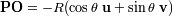 :
:
![|_ PO 3 PO.OL OL _| dG = Gm |_ ------- -------------- ----- _| m D3 D2 D3 Gm--- = 3 [- R (cos h u + sin h v) + 3R cos h u] D GmR = --------[2 cos h u - sin h v] D3](../../../../images/marea/images-TeX4ht/marea45x.png)
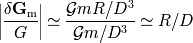
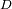 al cuerpo que provoca la marea.
al cuerpo que provoca la marea.
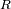 del objeto afectado.
del objeto afectado.