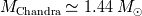Objetivos
Objetivos
Cuando la masa del núcleo de la estrella alcanza
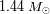
, el núcleo llega a una fase de la evolución durante la cual la presión de Fermi de los electrones no consigue
mantener la estrella.
Presión de degeneración relativista
Cuando la masa de una enana blanca crece, con un radio cada vez mas pequeño, su masa
volúmica y su temperatura aumentan. Hay que considerar en este caso los electrones como
relativistas. La presión, siempre definida como un flujo de cantidad de movimiento, se vuelve
en este caso igual a (con

):
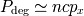
Presión de degeneración relativista
Se deduce la expresión de la presión de degeneración relativista.
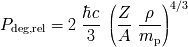
donde
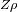
es la carga volúmica y
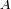
el número de masa de átomos presentes.
Colapso
El balance del equilibro del objeto tiene que ser realizado entre la presión de degeneración
relativista y la presión gravitacional :
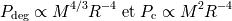
Los dos términos tienen la misma dependencia en función del radio : contrariamente al caso
clásico, una disminución del radio no permite a la presión de Fermi de sostener la estrella. En
cambio, la dependencia en función de la masa desfavorece la presión de Fermi : si la masa del
objeto es demasiado grande, la presión no puede sostener la estrella.
Masa de Chandrasekhar
La aplicación numérica muestra que más allá de
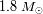
, la estrella no se puede mantener. Una simulación más precisa da una masa límite, llamada
masa de Chandrasekhar, más de la cual la estrella se colapsa debido a la ausencia de apoyo de
la presión de degeneración de los electrones :
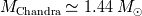
Si la masa del núcleo central de una estrella es superior a este valor, la estrella colapsa hacia
una
estrella de neutrones.

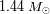 , el núcleo llega a una fase de la evolución durante la cual la presión de Fermi de los electrones no consigue
mantener la estrella.
, el núcleo llega a una fase de la evolución durante la cual la presión de Fermi de los electrones no consigue
mantener la estrella.  ):
):
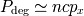
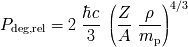
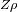 es la carga volúmica y
es la carga volúmica y
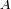 el número de masa de átomos presentes.
el número de masa de átomos presentes.
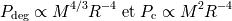
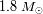 , la estrella no se puede mantener. Una simulación más precisa da una masa límite, llamada
masa de Chandrasekhar, más de la cual la estrella se colapsa debido a la ausencia de apoyo de
la presión de degeneración de los electrones :
, la estrella no se puede mantener. Una simulación más precisa da una masa límite, llamada
masa de Chandrasekhar, más de la cual la estrella se colapsa debido a la ausencia de apoyo de
la presión de degeneración de los electrones :