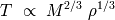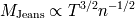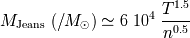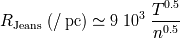Objetivos
Objetivos
¿ Cuáles son las condiciones necesarias para que una nube se contracte ? El criterio de Jeans da una respuesta
ya que une la masa o el radio límite de la nube a su densidad partícula y a su temperatura.
Perturbación
Una nube se colapsa si, perturbada, su energía mecánica es negativa :
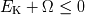
Se deduce una relación sobre la masa límite de la nube, en función de la temperatura (para
la agitación cinética) y de la densidad (para la contracción). Una masa superior a la masa
límite implica una contracción de la nube.
Se supone el medio homogeno y uniforme. La relacion entre la masa y el radio es
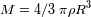
. En el caso límite, se deduce la desigualdad entre la energia cinetica y la potencial :
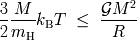
Vamos proseguir el cálculo, interesándonos a la dependencia en función de las variables.
Permitirá facilitar los cálculos y deshacerse de las constantes numéricas que no están
correctamente estimadas en la aproximación simplificada. Sustituyendo
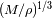
à
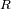
, el caso límite de la desigualdad precedente da una dependencia :
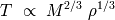

Masa de Jeans
Se deduce la masa límite de la nube, llamada
masa de Jeans. Depende de la temperatura y de
la densidad de la nube según la relación :
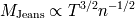
Cuanto más caliente está la nube más masiva puede ser antes de colapsarse : la presión
cinética ayuda a matenerse. Al contrario, cuanto más densa más la masa de Jeans disminuye
debido al potencial gravitacional.
En unidad de masa solar, la masa de Jeans es :
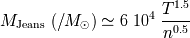

Radio de Jeans
El límite de colapso puede expresarse a través del radio de la nube, en función de la temperatura
de la nube y de su densidad.
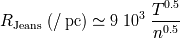

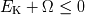
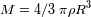 . En el caso límite, se deduce la desigualdad entre la energia cinetica y la potencial :
. En el caso límite, se deduce la desigualdad entre la energia cinetica y la potencial :
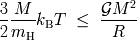
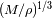 à
à
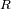 , el caso límite de la desigualdad precedente da una dependencia :
, el caso límite de la desigualdad precedente da una dependencia :