 Ejercicio 'Medida del periodo de Mercurio'
Ejercicio 'Medida del periodo de Mercurio'
Nivel * a **
Tiempo necesario :
1.5 heure
1)
Propagacion : Se recibe el eco de una señal radio emitida por el telescopio de Arecivo y reflejada por
Mercurio 616.125 s después de su emisión. Deducir la distancia Tierra-Mercurio

en la época de observación. representar la posicion relativa de los dos planetas y del Sol. ¿ Las
observaciones efectuadas en radio pueden ser realizadas con la luz visible?
ayuda
solución
2)
El campo de velocidad : Se localiza un punto
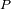
de la superficie visible de Mercurio por sus coordenadas cartesianas en el referencial
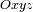
, donde
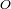
es el baricentro del planeta,
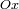
apunta hacia la Tierra y
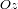
es paralelo al eje de rotación del planeta. Se define
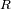
el radio de Mercurio,
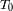
su periodo de revolución sideral y
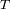
su periodo de rotación propia.
Dar las coordenadas del punto subterrestre [el punto de Mercurio que ve la Tierra en el
zénit].
Demostrar que la componente radial (colinear al eje Tierra-Mercurio) de la velocidad de arrastre de
rotación sólo depende de una de las componentes de la posición
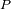
.
ayuda
ayuda
solución
3)
Análisis tiempo-frecuencia del eco radar :
¿ Qué regiones de la superficie contribuyen al inicio (
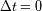
) y al final (
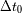
) de la señal del eco? Determinar la duración total teórica
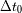
del eco. Representar el aspecto de las líneas de iso-atraso (líneas que presentan el mismo
atraso)
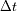
sobre el mapa de Mercurio [
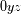
].
Se define
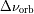
el desplazamiento Doppler de la señal reflejada en el punto subterrestre. ¿ Qué regiones contribuyen al
ensanchamiento Doppler extremo
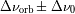
de la señal ? Representar en el mapa de Mercurio el aspecto de las líneas de iso-frecuencia
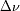
(con precisión de
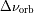
)
Calcular, para un punto de Mercurio de coordenadas
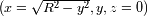
, el retraso
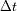
del eco y del desplazamiento espectral
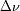
. Mostrar que se obtiene :
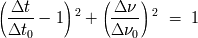 ayuda
solución
ayuda
solución
4)
El eco : El documento adjunto (Dyce et al. 1965) muestra el escalonamiento en frecuencia del eco en
función del retraso a la recepción. Comparar el retraso máximo teórico con el retraso medido e
interpretar. Deducir que la relación entre
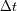
y
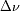
se reduce, para las medidas efectuadas, a
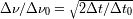
¿ Cómo interpretar las variaciones temporales de la intensidad de la señal?
Estimar
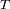
, el periodo de rotación propia de Mercurio.
Se define
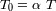
. ¿ Qué significado se puede dar a
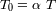
? ¿ De qué fracción simple de

se aproxima su valor ? ¿ Es una casualidad?
¿ Por qué los datos que presentan un mayor atraso no son las más fáciles de estudiar?
ayuda
ayuda
ayuda
solución
5)
La potencia del eco : ¿ Qué fracción de la señal intercepta Mercurio ? [Se busca un orden de magnitud.
Se supone que el flujo radar es homogéneo en el campo de ángulo sólido igual al lóbulo principal de
difracción].
Estimar, con un modelo simple, el numero de fotones incidentes necesario para recibir un fotón de
vuelta después de una reflexión en el punto subterrestre.
¿ Es sorprendente una potencia de emisión de 2 MW? [El impulso radar incidente es muy breve
:
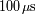
]
ayuda
ayuda
solución

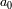
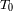
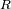

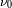

 en la época de observación. representar la posicion relativa de los dos planetas y del Sol. ¿ Las
observaciones efectuadas en radio pueden ser realizadas con la luz visible?
ayuda
solución
en la época de observación. representar la posicion relativa de los dos planetas y del Sol. ¿ Las
observaciones efectuadas en radio pueden ser realizadas con la luz visible?
ayuda
solución
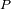 de la superficie visible de Mercurio por sus coordenadas cartesianas en el referencial
de la superficie visible de Mercurio por sus coordenadas cartesianas en el referencial
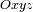 , donde
, donde
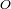 es el baricentro del planeta,
es el baricentro del planeta,
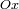 apunta hacia la Tierra y
apunta hacia la Tierra y
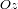 es paralelo al eje de rotación del planeta. Se define
es paralelo al eje de rotación del planeta. Se define
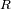 el radio de Mercurio,
el radio de Mercurio,
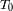 su periodo de revolución sideral y
su periodo de revolución sideral y
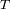 su periodo de rotación propia.
su periodo de rotación propia.
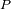 .
ayuda
ayuda
solución
.
ayuda
ayuda
solución
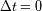 ) y al final (
) y al final (
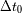 ) de la señal del eco? Determinar la duración total teórica
) de la señal del eco? Determinar la duración total teórica
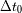 del eco. Representar el aspecto de las líneas de iso-atraso (líneas que presentan el mismo
atraso)
del eco. Representar el aspecto de las líneas de iso-atraso (líneas que presentan el mismo
atraso)
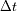 sobre el mapa de Mercurio [
sobre el mapa de Mercurio [
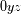 ].
].
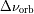 el desplazamiento Doppler de la señal reflejada en el punto subterrestre. ¿ Qué regiones contribuyen al
ensanchamiento Doppler extremo
el desplazamiento Doppler de la señal reflejada en el punto subterrestre. ¿ Qué regiones contribuyen al
ensanchamiento Doppler extremo
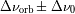 de la señal ? Representar en el mapa de Mercurio el aspecto de las líneas de iso-frecuencia
de la señal ? Representar en el mapa de Mercurio el aspecto de las líneas de iso-frecuencia
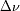 (con precisión de
(con precisión de
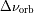 )
)
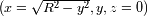 , el retraso
, el retraso
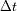 del eco y del desplazamiento espectral
del eco y del desplazamiento espectral
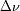 . Mostrar que se obtiene :
. Mostrar que se obtiene :
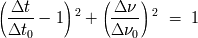
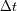 y
y
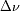 se reduce, para las medidas efectuadas, a
se reduce, para las medidas efectuadas, a
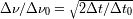 ¿ Cómo interpretar las variaciones temporales de la intensidad de la señal?
¿ Cómo interpretar las variaciones temporales de la intensidad de la señal?
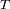 , el periodo de rotación propia de Mercurio.
, el periodo de rotación propia de Mercurio.
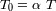 . ¿ Qué significado se puede dar a
. ¿ Qué significado se puede dar a
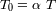 ? ¿ De qué fracción simple de
? ¿ De qué fracción simple de
 se aproxima su valor ? ¿ Es una casualidad?
se aproxima su valor ? ¿ Es una casualidad?
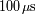 ]
ayuda
ayuda
solución
]
ayuda
ayuda
solución