Réalisations
Une loi de probabilité est déterministe. Mais ses réalisations sont ... aléatoires. C'est seulement avec un nombre élevé de réalisations que l'ensemble de ces réalisations retrace fidèlement la loi de probabilité. Si le nombre de réalisations est petit, on n'observe rien d'identifiable.
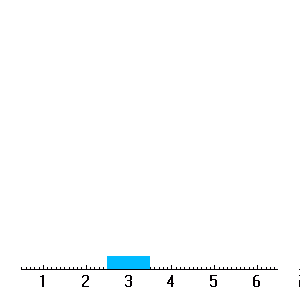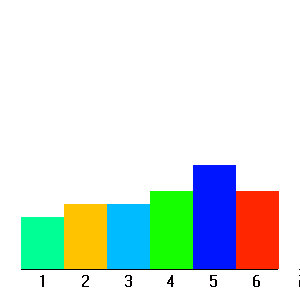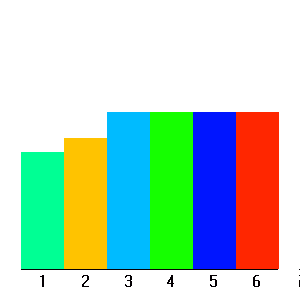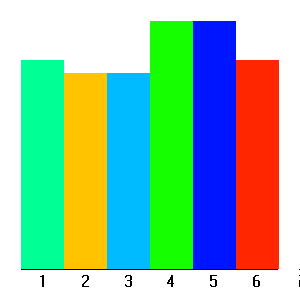
Loi uniforme, tirage d'un dé.
Crédit :
ASM
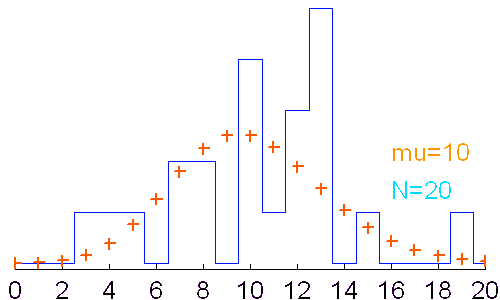
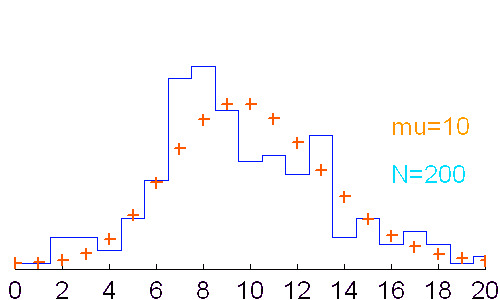
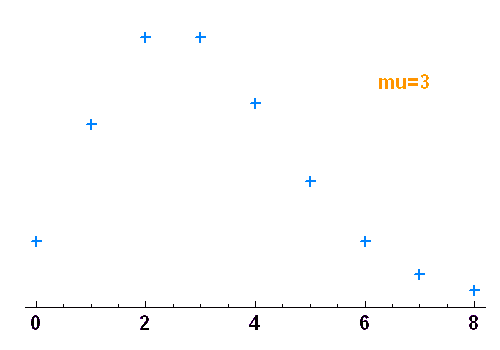
Réalisations d'un phénomène aléatoire obéissant à la loi de Poisson (moyenne = 10). Avec un nombre N de tirages peu élevé, la distribution des valeurs (courbe en bleu) ne ressemble que de très loin à la fonction de probabilité attendue (croix en rouge).
Crédit :
ASM
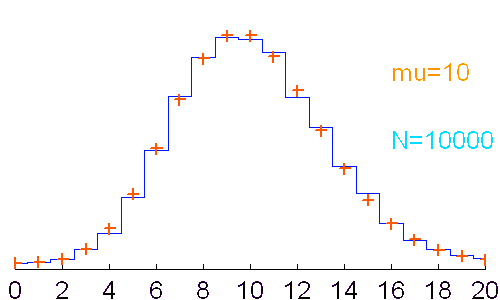
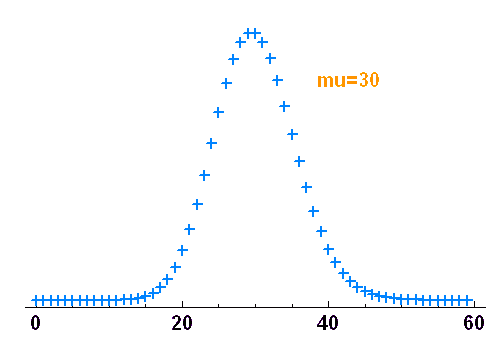
Réalisations d'un phénomène aléatoire obéissant à la loi de Poisson. Avec un nombre de tirages élevé, la distribution des valeurs trace convenablement la fonction de probabilité.
Crédit :
ASM
Estimations
Estimation de la moyenne et de l'écart type d'une loi. La moyenne peut être estimée de diverses façons, et la meilleure façon d'estimer une moyenne dépend de la loi de probabilité.
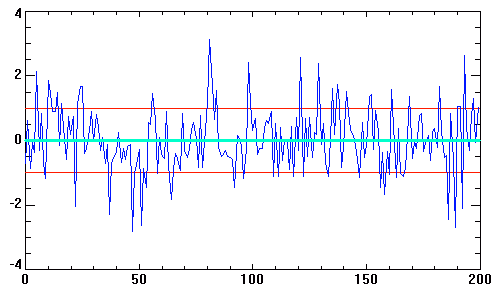
Moyenne (trait bleu ciel) et écart-type (droites de part et d'autre de la moyenne) pour un bruit blanc.
Crédit :
ASM
 Prérequis
Prérequis
Notions élémentaires de statistiques
 Objectifs
Objectifs
La définition d'un bruit repose sur ses propriétés statistiques. Cette page rappelle des notions simples de statistiques, en distinguant les lois de probabilité, leurs réalisations, et l'estimation de paramètres statistiques.
Loi de probabilité
La loi de probabilité d'une variable aléatoire 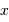 va être donnée par
va être donnée par 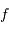 sa densité de probabilité, ou bien
sa densité de probabilité, ou bien 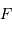 sa fonction de répartition
sa fonction de répartition 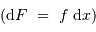 .
.
Parmi les moments centrés associés,
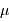 la moyenne et
la moyenne et 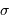 l'écart-type sont respectivement définis par :
l'écart-type sont respectivement définis par :
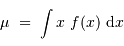
et :
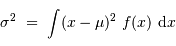
(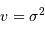 est la variance).
est la variance).
Une loi statistique possède des propriétés particulières, qui caractérisent tel ou tel phénomène : une loi poissonnienne (discrète) rend compte de l'arrivée d'événements indépendants, une loi gaussienne est souvent issue de l'addition d'un grand nombre de phénomènes indépendants...
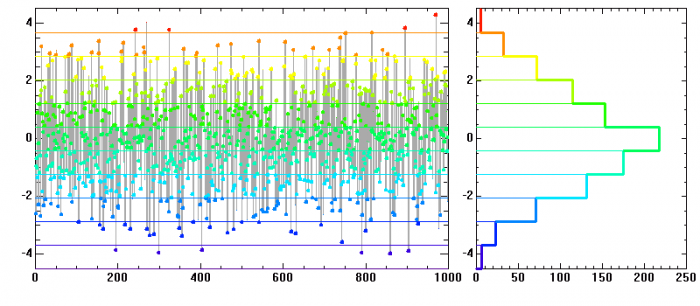
Réalisation d'une loi normale. L'histogramme se rapproche de la loi de probabilité.
Crédit :
ASM
Réalisations
La réalisation d'une loi de probabilité est aléatoire : un tirage de dés, réalisé 6 fois, ne conduira pas nécessaire à l'obtention une fois et une seule de chaque chiffre de 1 à 6. Plus le nombre de réalisations est grand, meilleur est l'accord entre l'observation de ces réalisations et la loi de probabilité.
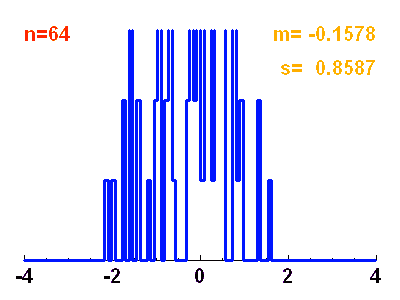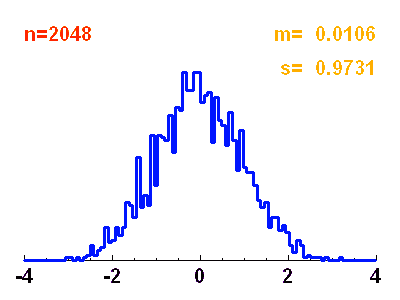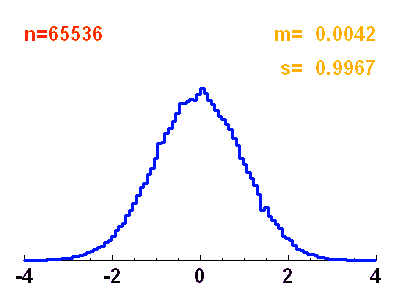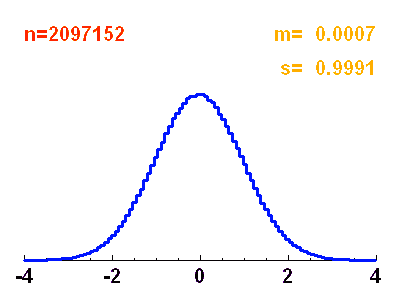
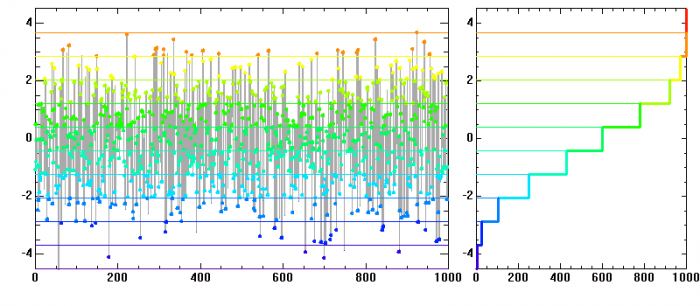
Histogramme d'une distribution de
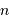
points obéissant à une loi normale de moyenne nulle et écart-type unité. Ce n'est qu'avec un très grand nombre de points que les réalisations représentent précisément la courbe théorique gaussienne.
Crédit :
ASM
Loi statistique et réalisation
L'animation ci-joint montre comment est réalisée en pratique une distribution normale. Ce n'est qu'avec un très grand nombre de tirages que l'histogramme des réalisations ressemble vraiment à la distribution statistique.


Mesure de bruits
Les appliquettes ci-jointes dévoilent des signaux temporels bruités, affectés ou non d'une lente dérive. On se propose d'en mesurer le bruit et le
rapport signal à bruit.
Se servir des appliquettes pour :
- Déterminer la moyenne du signal.
- Le cas échéant, corriger de la dérive.
- Mesurer l'écart-type, en appliquant sa définition et la fonction ajustement.
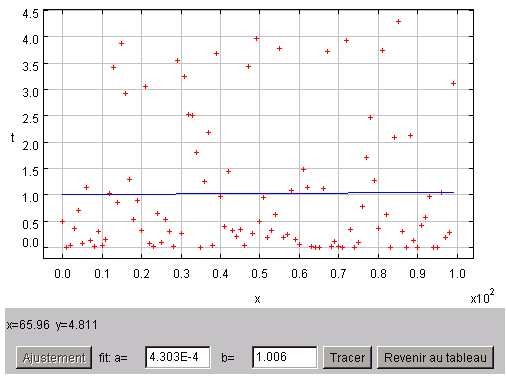
Avec l'appliquette, on calcule
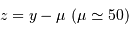
et puis
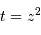
. L'ajustement donne un écart-type de 1.
Crédit :
ASM
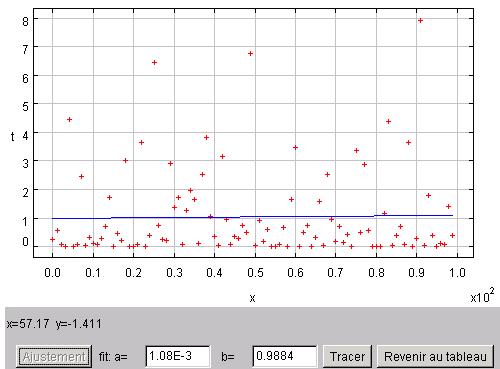
On remarque que la distribution des valeurs de
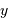
n'est pas uniforme autour d'une valeur moyenne, mais suis une relation linéaire. Il est nécessaire de soustraire la pente. On estime cette dernière avec l'appliquette, et on calcule alors la valeur centrée sur 0
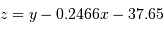
et puis
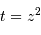
. L'ajustement donne un écart-type de 1.04.
Crédit :
ASM
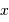 suit une loi de Poisson de moyenne
suit une loi de Poisson de moyenne 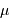 si la probabilité pour réaliser
si la probabilité pour réaliser 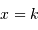 vaut
vaut 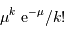





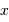 va être donnée par
va être donnée par 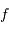 sa densité de probabilité, ou bien
sa densité de probabilité, ou bien 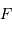 sa fonction de répartition
sa fonction de répartition 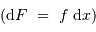 .
.
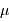 la moyenne et
la moyenne et 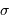 l'écart-type sont respectivement définis par :
l'écart-type sont respectivement définis par :
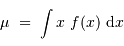
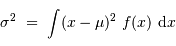
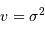 est la variance).
est la variance).


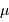 de la densité de probabilité de sa mesure
de la densité de probabilité de sa mesure 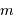 . Avec
. Avec 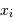 les réalisations d'une variable aléatoire, on a accès seulement à :
les réalisations d'une variable aléatoire, on a accès seulement à :
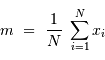
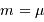 . En fait, c'est de mieux en mieux réalisé lorsque
. En fait, c'est de mieux en mieux réalisé lorsque 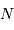 devient très grand.
devient très grand.
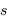 est mesurable par :
est mesurable par :
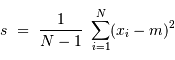
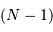 au dénominateur car
au dénominateur car 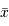 a déjà été obtenu à l'aide des
a déjà été obtenu à l'aide des 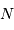 mesures, et il ne reste plus que
mesures, et il ne reste plus que 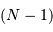 valeurs indépendantes pour estimer
valeurs indépendantes pour estimer 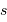 .
.
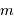 et
et 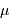 vaut typiquement
vaut typiquement 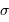 .
.

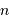 points obéissant à une loi normale de moyenne nulle et écart-type unité. Ce n'est qu'avec un très grand nombre de points que les réalisations représentent précisément la courbe théorique gaussienne.
points obéissant à une loi normale de moyenne nulle et écart-type unité. Ce n'est qu'avec un très grand nombre de points que les réalisations représentent précisément la courbe théorique gaussienne.


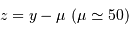 et puis
et puis 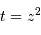 . L'ajustement donne un écart-type de 1.
. L'ajustement donne un écart-type de 1.

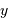 n'est pas uniforme autour d'une valeur moyenne, mais suis une relation linéaire. Il est nécessaire de soustraire la pente. On estime cette dernière avec l'appliquette, et on calcule alors la valeur centrée sur 0
n'est pas uniforme autour d'une valeur moyenne, mais suis une relation linéaire. Il est nécessaire de soustraire la pente. On estime cette dernière avec l'appliquette, et on calcule alors la valeur centrée sur 0 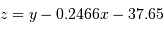 et puis
et puis 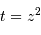 . L'ajustement donne un écart-type de 1.04.
. L'ajustement donne un écart-type de 1.04.