
|
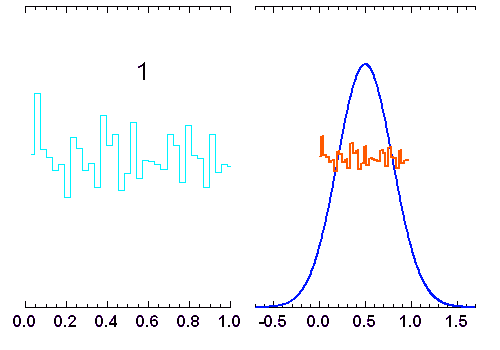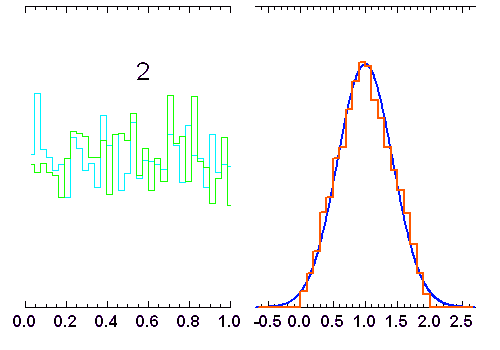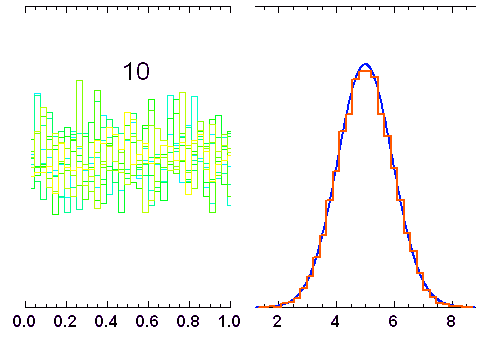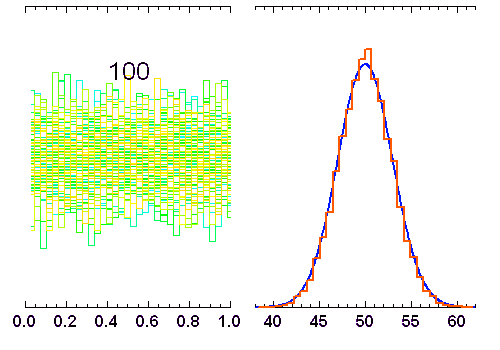
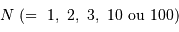 variables indépendantes, obéissant à une loi de distribution uniforme (entre 0 et 1). Lorsque
variables indépendantes, obéissant à une loi de distribution uniforme (entre 0 et 1). Lorsque 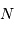 augmente, la distribution tend vers une loi gaussienne de moyenne
augmente, la distribution tend vers une loi gaussienne de moyenne 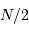 et écart type
et écart type 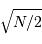 (courbe rouge). Pour
(courbe rouge). Pour 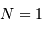 , la distribution reste bien sûr uniforme,
pour
, la distribution reste bien sûr uniforme,
pour 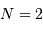 elle garde une allure triangulaire.
elle garde une allure triangulaire.
La superposition de plusieurs variables aléatoires indépendantes les unes des autres conduit à une loi normale. C'est l'une des conséquences du théorème de la limite centrale. L'animation ci-jointe en montre un exemple.
Exemples de distributions gaussiennes.
Si un bruit est gaussien, la probabilité qu'il s'écarte de plus ou moins 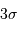 de la valeur moyenne est très faible. Cette propriété est mise à profit pour identifier le signal du bruit, mais ne marche que si le bruit est vraiment gaussien.
de la valeur moyenne est très faible. Cette propriété est mise à profit pour identifier le signal du bruit, mais ne marche que si le bruit est vraiment gaussien.