
|
Loi de probabilité ; éléments de statistique
Le théorème de la limite central implique qu'un bruit résultant de l'action indépendante de différents facteurs physiquesobéit à la loi de probabilité, dite loi normale :
![f(x) \ = \ {1\over \sqrt{2\pi}\sigma}\ \exp \left[ -{(x-\mu)^2\over 2 \sigma^2} \right]](../pages_analyser/equations_bruit-gaussien/equation9.png)
avec 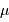 la moyenne et
la moyenne et 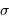 l'écart-type. Un tel bruit est dit gaussien.
l'écart-type. Un tel bruit est dit gaussien.
Pour une loi gaussienne, la probabilité d'observer un signal s'écartant de 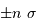 par rapport à la valeur moyenne décroît rapidement avec
par rapport à la valeur moyenne décroît rapidement avec 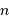 ;
99.7 % des réalisations du signal s'écartent de moins de
;
99.7 % des réalisations du signal s'écartent de moins de 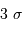 de la moyenne.
de la moyenne.
| n | 1 | 2 | 3 | 4 |
| % | 69.2 | 95.4 | 99.7 | 99.99 |
Probabilité d'avoir une valeur dans l'intervalle ![[-n\ \sigma, \ n \ \sigma]](../pages_analyser/equations_bruit-gaussien/equation15.png) pour un bruit gaussien.
pour un bruit gaussien.
De ce qui précède, peut-on dire qu'un événement qui s'écarte de plus de 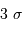 de la moyenne est sûrement dû à un signal et non à un bruit, et l'identifier comme tel ?
de la moyenne est sûrement dû à un signal et non à un bruit, et l'identifier comme tel ?
On considère une détection sûre lorsqu'elle dépasse un seuil de 4 ou 5 fois l'écart-type. Mais, la difficulté réside souvent dans le fait que la nature d'un bruit n'est pas exactement gaussienne, ou que des signaux parasites non identifiés compliquent l'interprétation d'un signal.
L'analyse fréquentielle d'un bruit gaussien ne montre aucune composante privilégiée. Pour cette raison, on parle d'un bruit blanc.