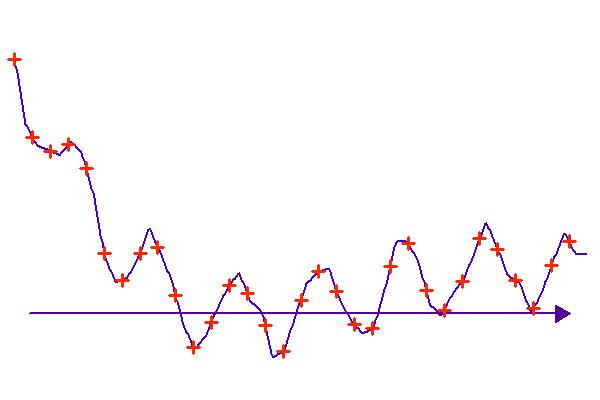
Fonction continue et signal discret associé.
Crédit :
ASM
Continu / discret
Un signal continu n'existe pas : décrire le continu nécessite une infinité de valeurs. Tout signal est échantillonné, càd décrit sur un nombre discret de valeurs.
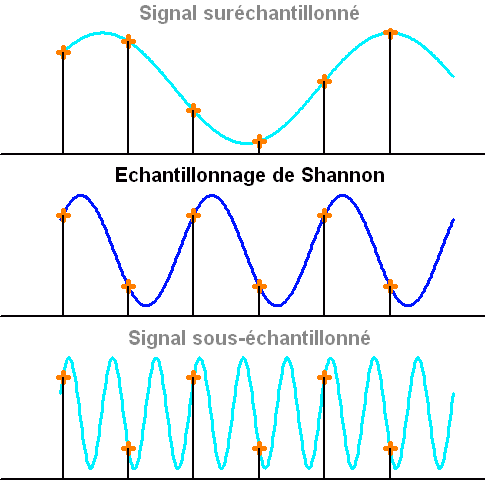
Un signal simple est échantillonné à la limite de Shannon avec 2 points par période. L'information d'un signal sous-échantillonné est perdue.
Crédit :
ASM
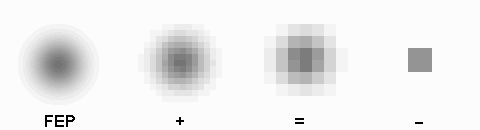
L'image initiale (cadre de gauche) est échantillonnée sur un nombre décroissant de pixels. Toute l'information utile est préservée dès lors que la fonction d'étalement du point est convenablement échantillonnée (=). Trop d'informations est inutile (+), et pas assez est destructif (-).
Crédit :
ASM
Échantillonnage de Shannon
Un détecteur ayant une résolution limite (spatiale ou temporelle), un signal physique est nécessairement échantillonné. Même si une observation avec ce détecteur semble prendre des valeurs continues, elle peut être traduite par une série finie de valeurs, correspondant à un échantillonnage discret.
Une bonne observation nécessite de ne pas dégrader la résolution du signal par ce phénomène d'échantillonnage, ce qu'exprime la condition d'échantillonnage de Shannon, qui s'applique aussi pour un signal 2-D.
Coupure
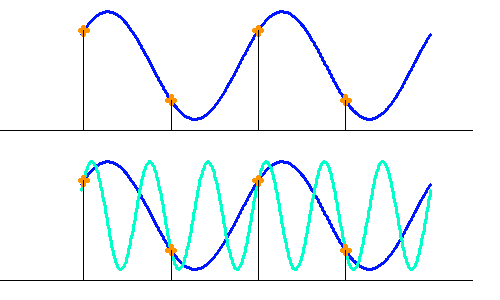
Il est nécessaire d'échantillonner au moins 2 points par période. L'échantillonnage définit ainsi une valeur maximale des fréquences analysables.
Au-delà de la fréquence de coupure, un signal de fréquence plus rapide que la fréquence de coupure peut se confondre avec un signal de pulsation moindre.
Crédit :
ASM
Echantillonnage et coupure
Le pas d'échantillonnage détermine la résolution maximale en fréquence. Au delà de la fréquence de coupure, échantillonnée sur 2 points par période, l'information est perdue. Autrement dit, la fréquence de coupure définie selon Fourier et le théorème de Shannon rendent compte du même phénomène.
Echantillonnage
Tout signal, spatial ou temporel, est limité en fréquence, à cause du processus d'observation. Il peut être codé sur une distribution discrète de valeurs. Ce processus de discrétisation est nommé échantillonnage.
Théorème de Shannon
Le critère de Shannon énonce qu'un signal doit avoir sa fréquence maximale échantillonnée sur au-moins 2 pixels afin de ne subir aucune dégradation.
En pratique, il faut :
- 2 acquisitions temporelles par période pour un signal temporel périodique
- 2 pixels par élément de résolution spatiale pour un signal spatial
La justification de ce critère est liée à l'analyse fréquentielle, par transformée de Fourier : en appliquant le critère de Nyquist, les fréquences sont restituées convenablement jusqu'à la fréquence de coupure.
 Choix d'un détecteur
Choix d'un détecteur
Difficulté : ☆
Temps : 10 min
Un télescope de la classe 4-m, dans une configuration ouverte à f/2, est installé dans un site dont le meilleur seeing est aux alentours de 0.5" en lumière visible. Une caméra CCD installée pour des programmes d'imagerie est spécifiée pour imager sans perdre d'éléments d'information.
Question 1)
Quel paramètre de la caméra est crucial pour satisfaire la spécification donnée ?
L'ouverture du faisceau est déterminée, ainsi que la résolution angulaire. Ceci permet de déterminer la résolution spatiale dans le plan focal.
Question 2)
Sur catalogue, on trouve des caméras avec des pixels de 9, 15 ou 25 microns. Quel choix effectuer ?
Question 3)
Un système d'optique adaptative permet d'atteindre la limite théorique de diffraction dans l'IR à 2 microns. Sachant qu'il n'existe pas de caméra avec des pixels plus petits que 9 micromètres, quel paramètre de la chaîne de collecte du signal doit évoluer ?
Déterminer la tache de diffraction à 2 micromètres.
Identifier les paramètres fixes, de ceux qui le sont moins...
 Signal sismique
Signal sismique
Difficulté : ☆
Temps : 10 min
On cherche à caractériser un spectre d'oscillations stellaires. La période minimale des oscillations stellaires est de 4 minutes, et on souhaite distinguer des fréquences avec une résolution de 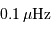 .
.
Question 1)
Estimer la durée totale nécessaire pour ce programme.
[1 points]
Question 2)
Déterminer l'échantillonnage temporel optimal, qui permette de ne pas filtrer les hautes fréquences et minimise le nombre final de données.
[1 points]
Question 3)
Les séquences d'observation du satellite COROT (projet CNES) sont-elles en accord, avec un point de mesure toutes les 32 s et 150 jours d'observation continue sur une cible stellaire ?
[1 points]
- Question 1
Aide :
L'ouverture du faisceau est déterminée, ainsi que la résolution angulaire. Ceci permet de déterminer la résolution spatiale dans le plan focal.
Solution :
L'ouverture du faisceau étant déterminée, la focale du télescope est connue (8 m) ainsi que la résolution angulaire, limité par le seeing 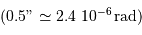 , la taille linéaire dans le plan focal est fixée :
, la taille linéaire dans le plan focal est fixée :
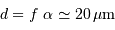
- Question 2
Solution :
La taille des pixels doit être au moins moitié moindre que la tache de seeing, il faut donc des pixels de 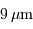 .
.
- Question 3
Aide :
Déterminer la tache de diffraction à 2 micromètres.
Aide :
Identifier les paramètres fixes, de ceux qui le sont moins...
Solution :
La tache de diffraction vaut 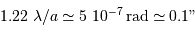 . Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.
. Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.
Comme le diamètre du télescope est fixée, de même que la taille minimale des pixels, la seule variable d'ajustement est l'ouverture du faisceau. Elle doit être diminuée d'un facteur au-moins 5, passant de f/4 à f/20.


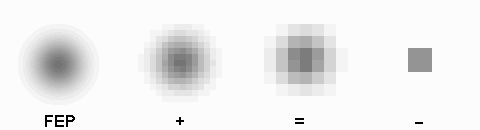

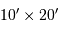 avec une résolution de 0.6",
il faut une caméra de taille (en pixels) :
avec une résolution de 0.6",
il faut une caméra de taille (en pixels) :
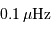 .
.
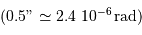 , la taille linéaire dans le plan focal est fixée :
, la taille linéaire dans le plan focal est fixée :
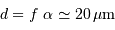
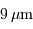 .
.
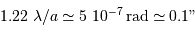 . Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.
. Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.