Traitement de l'image

Observer

Rapport signal à bruit du signal d'obscurité

Le signal d'obscurité doit être enregistré avec un rapport signal à bruit meilleur que celui des images à traiter.

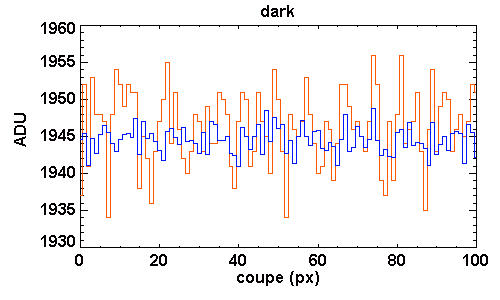
sommedark.png
Coupe le long de 2 images d'obscurité, l'une élémentaire, l'autre résultant de la moyenne de 20 images élémentaires. L'amélioration du rapport signal à bruit est bénéfique pour le traitement des images à suivre.
Crédit : ASM

Apprendre

objectifsObjectifs

Les étapes de correction des signaux de courant d'obscurité et de champ plat ne se font pas sans bruit. Le but de cette page est d'estimer les performances de ces opérations, et de montrer que les signaux de courant d'obscurité et de champ plat doivent être connus avec un rapport signal à bruit (bien) meilleur que celui du signal seul.

Courant d'obscurité

La correction consiste à soustraire au signal le signal d'obscurité. Ce dernier est acquis lors d'une pose longue, sans source. Cette soustraction s'exprime par :

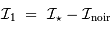
\mathcal{I}_1 \ = \ \mathcal{I}_\star - \mathcal{I} _{\mathrm{noir}}

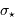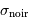Les bruits des signaux d'entrée sont respectivement \sigma_\star et \sigma _{\mathrm{noir}} (le bruit de la source comprend le bruit de photons). Non corrélés, il s'additionnent quadratiquement pour donner le bruit de la différence :

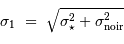
\sigma_1 \ = \ \sqrt{ \sigma_\star^2 + \sigma _{\mathrm{noir}}^2}

Le rapport signal à bruit s'écrit donc :

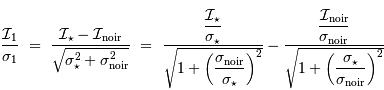
{ \mathcal{I}_1 \over \sigma_1}\ =\ { \mathcal{I}_\star - \mathcal{I} _{\mathrm{noir}} \over \sqrt{ \sigma_\star^2 + \sigma _{\mathrm{noir}}^2}} \ =\ {\displaystyle{ \mathcal{I}_\star \over \sigma_\star} \over \sqrt{1 +\left(\displaystyle{ \sigma _{\mathrm{noir}} \over \sigma_\star}\right)^2}} - {\displaystyle{ \mathcal{I} _{\mathrm{noir}} \over \sigma _{\mathrm{noir}}} \over \sqrt{1 +\left(\displaystyle{ \sigma_\star \over \sigma _{\mathrm{noir}}}\right)^2}}

Ceci montre que le rapport signal à bruit après correction du courant d'obscurité est moindre qu'avant correction :

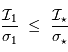
{ \mathcal{I}_1 \over \sigma_1}\ \le\ { \mathcal{I}_\star \over \sigma_\star}

Cette correction reste néanmoins nécessaire pour corriger certains effets structurels de la caméra.

Le cas 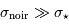\sigma _{\mathrm{noir}} \gg \sigma_\star où le bruit de courant d'obscurité domine apparaît très inintéressant : la performance de la correction sera d'autant bruitée. En revanche, si le signal d'obscurité est bien moins bruité que le signal astrophysique, càd 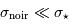\sigma _{\mathrm{noir}} \ll \sigma_\star, on récupère :

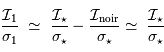
{ \mathcal{I}_1 \over \sigma_1}\ \simeq\ { \mathcal{I}_\star \over \sigma_\star} - { \mathcal{I} _{\mathrm{noir}} \over \sigma_\star} \simeq\ { \mathcal{I}_\star \over \sigma_\star}

Le rapport signal à bruit est très peu dégradé. Il est donc indispensable d'acquérir une bonne image très peu bruitée du courant d'obscurité.

Champ plat

La correction de champ plat consiste à diviser le signal 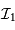\mathcal{I}_1 par le signal de champ plat normalisé (et éventuellement corrigé du courant d'obscurité). Le champ plat est acquis lors d'une pose sur une source la plus uniforme possible. La division s'exprime :

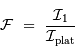
\mathcal{F} \ = \ { \mathcal{I}_1 \over \mathcal{I} _{\mathrm{plat}}}

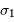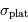Les bruits en entrée sont respectivement \sigma_1 et \sigma _{\mathrm{plat}}. Le bruit final dépend des bruits et signaux initiaux via :

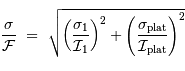
{ \sigma \over \mathcal{F}}\ =\ \sqrt{\left(\displaystyle{ \sigma_1 \over \mathcal{I}_1}\right)^2 + \left(\displaystyle{ \sigma _{\mathrm{plat}} \over \mathcal{I} _{\mathrm{plat}}}\right)^2}

Pour s'en convaincre, il suffit de différencier logarithmiquement la relation définissant 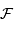\mathcal{F}. On peut donc réécrire le rapport signal à bruit :

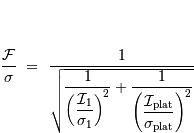
{ \mathcal{F} \over \sigma}\ =\ {1\over\sqrt{ \displaystyle{1 \over \left(\displaystyle{ \mathcal{I}_1 \over \sigma_1}\right)^2} + \displaystyle{1 \over \left(\displaystyle{ \mathcal{I} _{\mathrm{plat}} \over \sigma _{\mathrm{plat}}}\right)^2} }}

On remarque que cette correction dégrade nécessairement le rapport signal à bruit, car de toutes façons :

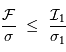
{ \mathcal{F} \over \sigma}\ \le \ { \mathcal{I}_1 \over \sigma_1}

Il est inintéressant d'avoir un champ plat très bruité, car la performance sera limitée au rapport signal à bruit du champ plat dans ce cas. En revanche, si le champ plat est peu bruité 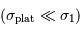( \sigma _{\mathrm{plat}} \ll \sigma_1), on obtient :

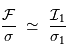
{ \mathcal{F} \over \sigma}\ \simeq \ { \mathcal{I}_1 \over \sigma_1}

Il est donc indispensable d'acquérir une image de champ plat la moins bruitée possible. Ceci peut nécessiter une longue durée d'observation sur une source artificielle uniforme.

Enfin, on remarque dans cette opération qu'un signal bruité est moins dégradé qu'un signal peu bruité. En effet, corriger un signal peu bruité nécessite une correction de qualité meilleure encore.

Simuler

Corrections

A l'aide de l'appliquette ci-jointe, assurer la correction du signal d'obscurité sur les images de Jupiter. La correspondance entre les noms de fichiers et les images est la suivante, selon le rang des lettres :

  1. f=flat : champ plat, j : image jovienne, d=dark : courant d'obscurité.
  2. s : SYMPA : projet de sismologie jovienne ; images enregistrées en 2004 au télescope de l'Observatoire San Pedro Martir au Mexique.
  3. e : image élémentaire ; s = image sommée
  4. N : numéro de l'image (facultatif)

Correction de l'image Jovienne application.png

Réaliser les opérations de corrections du courant d'obscurité et du champ plat, et comparer les résultats par des coupes d'images. Voir le mode d'emploi de l'appliquette donné précédemment.

Rapport signal à bruit de différentes sources

Le tableau de l'appliquette ci-jointe donne les signaux moyens, par pixel, du courant d'obscurité (dark) et du champ plat (flat), ainsi que de diverses sources plus ou moins brillantes. On cherche à déterminer le rapport signal à bruit des observations. Le bruit de lecture est estimé à 20 e-.

application.png

En fonction de ce qui précède, comparer l'évolution des rapports signaux à bruits des diverses sources.