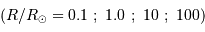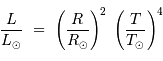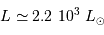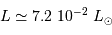Puissance totale rayonnée
 Objectifs
Objectifs
Etablir le bilan de la puissance rayonnée par un corps noir stellaire.
Quelle puissance rayonne une étoile de température d'équilibre 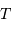 , assimilable à un corps
noir de température
, assimilable à un corps
noir de température 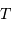 , supposée sphérique de rayon
, supposée sphérique de rayon 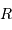 ? La réponse
nécessite d'intégrer la luminance spectrale du corps noir sur toute sa
surface, dans toutes les directions, à toute longueur d'onde.
? La réponse
nécessite d'intégrer la luminance spectrale du corps noir sur toute sa
surface, dans toutes les directions, à toute longueur d'onde.
Le calcul aboutit à la puissance :
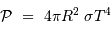
avec la constante de Stefan : 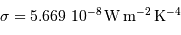 .
.
Puissance totale rayonnée
On peut justifier rapidement la présence des termes 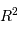 et
et 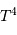 dans cette puissance totale rayonnée.
En effet, l'intégration de la luminance spectrale, spatiale, angulaire et spectrale :
dans cette puissance totale rayonnée.
En effet, l'intégration de la luminance spectrale, spatiale, angulaire et spectrale :
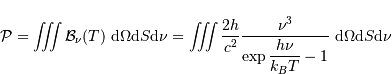
implique, pour la dépendance en fonction du rayon, un terme proportionnel à la surface
stellaire, variant donc comme 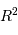 , et pour le terme de température, un
terme proportionnel à
, et pour le terme de température, un
terme proportionnel à 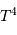 , mis en évidence par le changement de
variable
, mis en évidence par le changement de
variable 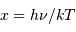 , qui conduit à :
, qui conduit à :
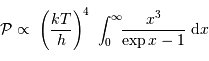
Les termes non explicités dans cette équation ne dépendent pas de la
température, pas plus que l'intégrale sur la variable 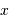 , qui n'est
plus qu'un simple nombre
, qui n'est
plus qu'un simple nombre 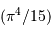 .
.
La loi en 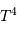 entraîne une grande diversité dans la vie des étoiles.
Deux étoiles de rayons analogues mais avec des températures variant du simple au
quintuple (4000 - 20000 K p.ex.) vont avoir des luminosités dans un rapport de
625, donc déjà des couleurs et luminosités très différents. Mais il s'ensuit
également des conséquences très fortes sur leurévolution.
entraîne une grande diversité dans la vie des étoiles.
Deux étoiles de rayons analogues mais avec des températures variant du simple au
quintuple (4000 - 20000 K p.ex.) vont avoir des luminosités dans un rapport de
625, donc déjà des couleurs et luminosités très différents. Mais il s'ensuit
également des conséquences très fortes sur leurévolution.
 Rayon stellaire
Rayon stellaire
Difficulté : ☆☆☆
Temps : 45min
La puissance rayonnée par une étoile, assimilée à un corps noir de rayon 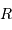 et température
et température 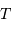 , varie comme :
, varie comme :
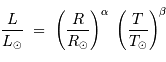
avec 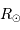 ,
, 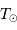 et
et 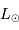 respectivement les rayon, température effective et luminosité du soleil.
respectivement les rayon, température effective et luminosité du soleil.
Question 1)
Rappeler les valeurs de 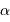 et
et 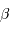
Voir la définition de la puissance rayonnée par un corps noir sphérique de rayon 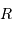 et
de température
et
de température 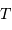
Question 2)
Une naine blanche présente une luminosité 100 fois inférieure à celle du Soleil, pour une température 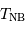 . Estimer son
rayon
. Estimer son
rayon 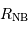 , en fonction des données solaires et de
, en fonction des données solaires et de 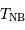 .
.
Il s'agit d'une simple application de la question précédente
Question 4)
Représenter sur le diagramme ci-joint les lignes iso-rayon, pour les étoiles de respectivement 0.1, 1 et 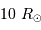 .
.
Diagramme HR
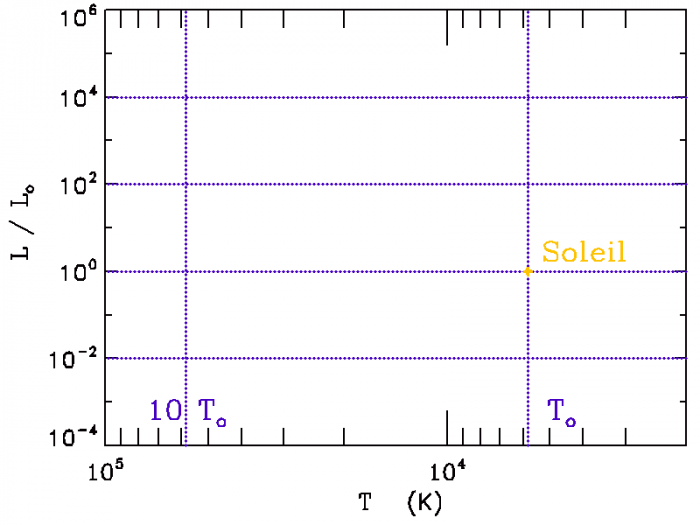
Diagramme HR : température en abscisse, luminosité (par rapport à la luminosité solaire) en ordonnée, avec en pointillé les
lignes iso-luminosité et iso-température (pour les températures
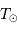
et
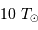
)
Crédit :
ASM
Le diagramme est en échelle log-log. Plutôt que de représenter les valeurs de température 1000, 10000 K par les logarithmes décimaux 3 et 4
selon une échelle linéaire, il présente 1000 et 10000 en échelle logarithmique.
Avec une telle échelle, une loi de puissance 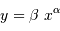 se traduit linéairement par
se traduit linéairement par
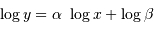
Une ligne iso-rayon relie dans le diagramme des étoiles de températures et luminosités variables, mais rayons identiques.
Question 5)
Situer sur ce diagramme une supergéante rouge de rayon 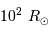 et une naine blanche de rayon
et une naine blanche de rayon 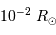 , de
température respective 4000 et 30 000 K.
, de
température respective 4000 et 30 000 K.
 Mesure de la température effective
Mesure de la température effective
Difficulté : ☆
Temps : 20 min
La loi de Stefan permet de calculer la température d'un corps noir à partir de sa luminosité et de sa taille. La difficulté est que ces deux termes dépendent de la distance de l'objet. L'exercice se propose de voir comment pallier cette difficulté, dès lors que l'on peut connaître, par interférométrie, le rayon angulaire de l'étoile. Par la suite, on note 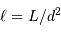 le flux relatif de l'étoile et
le flux relatif de l'étoile et 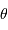 le rayon angulaire de l'étoile.
le rayon angulaire de l'étoile.
Question 1)
Comment 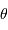 s'exprime-t-il en fonction du rayon
s'exprime-t-il en fonction du rayon 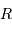 et de la distance
et de la distance 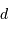 ?
?
[1 points]
L'approximation des petits angles est amplement justifiée.
Question 2)
Réécrire la relation de luminosité du corps noir en fonction des observables 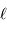 et
et 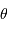 . En déduire que l'on peut relier la température de corps noir à des grandeurs directement mesurables.
. En déduire que l'on peut relier la température de corps noir à des grandeurs directement mesurables.
[2 points]
- Question 1
Aide :
Voir la définition de la puissance rayonnée par un corps noir sphérique de rayon 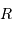 et
de température
et
de température 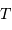
Solution :
La puissance du corps noir étant proportionnelle à 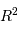 et
et 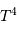 , il sort simplement :
, il sort simplement :
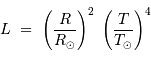
- Question 2
Aide :
Il s'agit d'une simple application de la question précédente
Solution :
L'égalité des luminosités se traduit par :
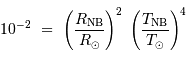
On en déduit :
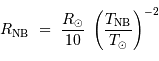
- Question 3
Solution :
L'application numérique de la question précédente donne
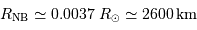
- Question 4
Aide :
Le diagramme est en échelle log-log. Plutôt que de représenter les valeurs de température 1000, 10000 K par les logarithmes décimaux 3 et 4
selon une échelle linéaire, il présente 1000 et 10000 en échelle logarithmique.
Avec une telle échelle, une loi de puissance 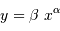 se traduit linéairement par
se traduit linéairement par
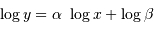
Aide :
Une ligne iso-rayon relie dans le diagramme des étoiles de températures et luminosités variables, mais rayons identiques.
Solution :
On s'intéresse à la ligne iso-rayon de rayon solaire. Elle est caractérisée par l'équation reliant température et luminosité s'exprimant :
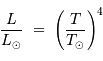
L'exposant 4 se traduit par une pente de 4 dans le diagramme log-log. La droite de pente 4 relie par exemple les points
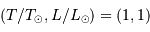 et
et 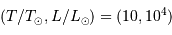 . Attention : la pente apparaît négative car l'axe des températures est orienté vers la gauche dans le diagramme HR usuel.
. Attention : la pente apparaît négative car l'axe des températures est orienté vers la gauche dans le diagramme HR usuel.
Diagramme HR
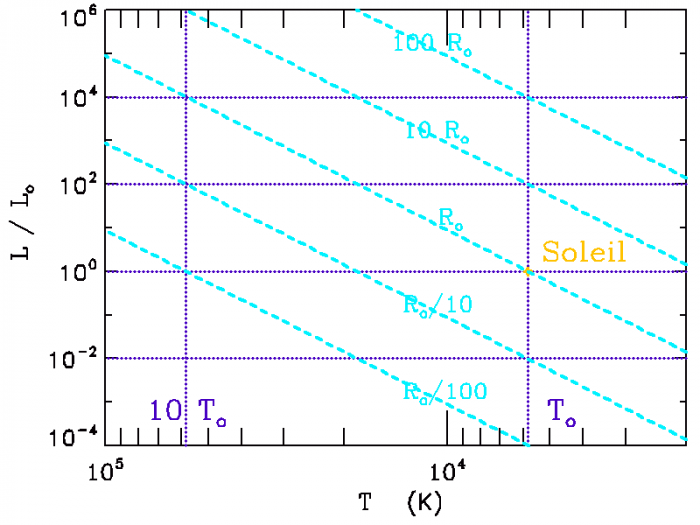
Diagramme HR avec lignes iso-rayon
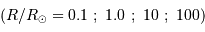
Crédit :
ASM
- Question 5
Solution :
L'application de l'expression donnant la luminosité
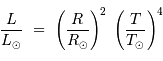
conduit, pour la géante rouge, à :
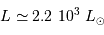
et pour la naine blanche :
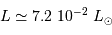
Diagramme HR
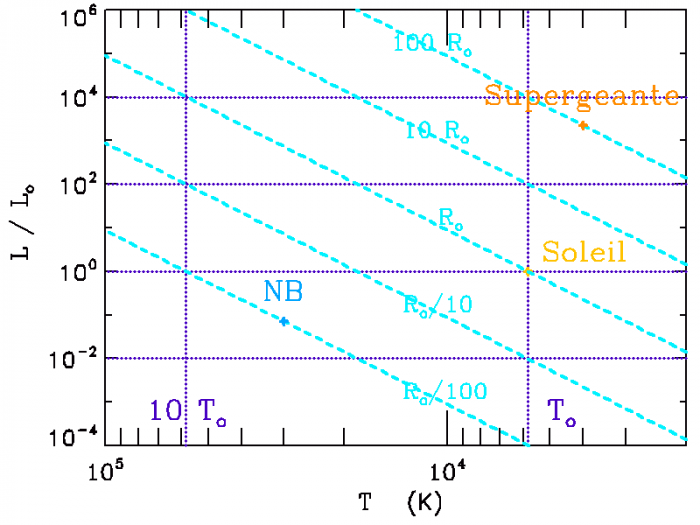
Crédit :
ASM
 Objectifs
Objectifs , assimilable à un corps
noir de température
, assimilable à un corps
noir de température 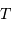 , supposée sphérique de rayon
, supposée sphérique de rayon 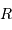 ? La réponse
nécessite d'intégrer la luminance spectrale du corps noir sur toute sa
surface, dans toutes les directions, à toute longueur d'onde.
? La réponse
nécessite d'intégrer la luminance spectrale du corps noir sur toute sa
surface, dans toutes les directions, à toute longueur d'onde.
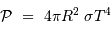
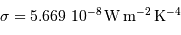 .
.
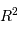 et
et 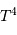 dans cette puissance totale rayonnée.
En effet, l'intégration de la luminance spectrale, spatiale, angulaire et spectrale :
dans cette puissance totale rayonnée.
En effet, l'intégration de la luminance spectrale, spatiale, angulaire et spectrale :
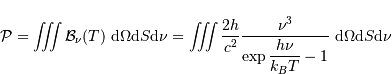
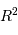 , et pour le terme de température, un
terme proportionnel à
, et pour le terme de température, un
terme proportionnel à 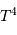 , mis en évidence par le changement de
variable
, mis en évidence par le changement de
variable 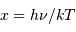 , qui conduit à :
, qui conduit à :
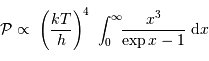
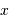 , qui n'est
plus qu'un simple nombre
, qui n'est
plus qu'un simple nombre 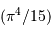 .
.
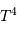 entraîne une grande diversité dans la vie des étoiles.
Deux étoiles de rayons analogues mais avec des températures variant du simple au
quintuple (4000 - 20000 K p.ex.) vont avoir des luminosités dans un rapport de
625, donc déjà des couleurs et luminosités très différents. Mais il s'ensuit
également des conséquences très fortes sur leurévolution.
entraîne une grande diversité dans la vie des étoiles.
Deux étoiles de rayons analogues mais avec des températures variant du simple au
quintuple (4000 - 20000 K p.ex.) vont avoir des luminosités dans un rapport de
625, donc déjà des couleurs et luminosités très différents. Mais il s'ensuit
également des conséquences très fortes sur leurévolution.
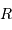 et température
et température 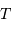 , varie comme :
, varie comme :
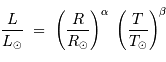
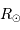 ,
, 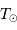 et
et 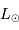 respectivement les rayon, température effective et luminosité du soleil.
respectivement les rayon, température effective et luminosité du soleil.
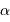 et
et 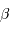
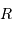 et
de température
et
de température 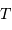
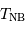 . Estimer son
rayon
. Estimer son
rayon 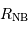 , en fonction des données solaires et de
, en fonction des données solaires et de 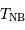 .
.
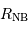 pour
pour 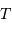 = 30000 K,
= 30000 K, 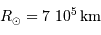 et
et 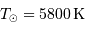 .
.
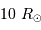 .
.

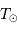 et
et 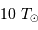 )
)
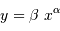 se traduit linéairement par
se traduit linéairement par
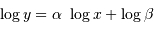
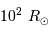 et une naine blanche de rayon
et une naine blanche de rayon 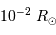 , de
température respective 4000 et 30 000 K.
, de
température respective 4000 et 30 000 K.
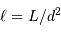 le flux relatif de l'étoile et
le flux relatif de l'étoile et 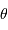 le rayon angulaire de l'étoile.
le rayon angulaire de l'étoile.
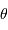 s'exprime-t-il en fonction du rayon
s'exprime-t-il en fonction du rayon 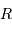 et de la distance
et de la distance 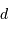 ?
?
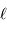 et
et 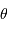 . En déduire que l'on peut relier la température de corps noir à des grandeurs directement mesurables.
. En déduire que l'on peut relier la température de corps noir à des grandeurs directement mesurables.
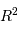 et
et 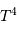 , il sort simplement :
, il sort simplement :
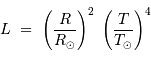
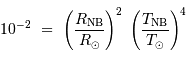
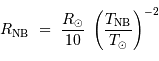
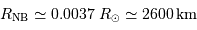
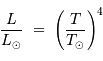
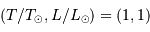 et
et 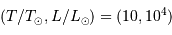 . Attention : la pente apparaît négative car l'axe des températures est orienté vers la gauche dans le diagramme HR usuel.
. Attention : la pente apparaît négative car l'axe des températures est orienté vers la gauche dans le diagramme HR usuel.