 Objectifs
Objectifs
Le corps correspond à un équilibre entre un corps de température 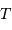 et un rayonnement de corps noir à cette même température.
et un rayonnement de corps noir à cette même température.
Thermalisation
L'exemple du soleil
permet de définir la température effective d'un corps noir, ou
température d'équilibre, ou température de brillance.
Le parcours de l'énergie au sein du soleil est, jusqu'aux couches
supérieures, une succession ininterrompue d'absorption et de réémission des photons initialement produits par les réactions nucléaires au centre de l'étoile, dans le domaine 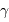 , jusqu'aux photons finalement émis, majoritairement dans les domaines UV, visible et IR.
, jusqu'aux photons finalement émis, majoritairement dans les domaines UV, visible et IR.
Arrivés dans la photosphère, les photons peuvent quitter le soleil, avec une distribution énergétique qui est celle du corps noir, de température donnée, que l'on appelle température effective.
Equilibre
En raison de l'équilibre entre le rayonnement de corps noir et la matière
du corps noir, il y a concordance entre cette température et celle du milieu
émetteur. D'après le second principe de la thermodynamique, les
couches atmosphériques plus profondes qui ont fourni l'énergie ne
peuvent être qu'à une température plus élevée. Il s'ensuit un certain
nombre de conséquences :
- La température effective correspond à la
température minimale rencontrée dans la partie supérieure de l'atmosphère
stellaire
- Le niveau de l'atmosphère que l'on voit, par définition celui dont sont
issus les photons, est de température très voisine à la température effective.
- Les niveaux inférieurs sont opaques, vu que le processus de
thermalisation entre matière et rayonnement y est à l'oeuvre
 Equilibre thermique d'une planète
Equilibre thermique d'une planète
Difficulté : ☆☆
Temps : 60 min
On s'intéresse au bilan radiatif d'une planète en orbite circulaire de rayon 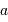 autour de son étoile.
On suppose l'espace interplanétaire vide, ce qui entraîne la conservation du flux stellaire intégrée sur toute surface entourant l'étoile. La rotation propre de la planète est suffisamment rapide pour que l'on puisse
considérer sa température
autour de son étoile.
On suppose l'espace interplanétaire vide, ce qui entraîne la conservation du flux stellaire intégrée sur toute surface entourant l'étoile. La rotation propre de la planète est suffisamment rapide pour que l'on puisse
considérer sa température 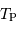 comme uniforme sur toute la surface. On néglige toute autre source
d'énergie que stellaire.
comme uniforme sur toute la surface. On néglige toute autre source
d'énergie que stellaire.
La planète réfléchit une fraction 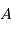 du rayonnement solaire, et en
absorbe une fraction
du rayonnement solaire, et en
absorbe une fraction 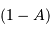 , où
, où 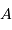 est l'albédo.
On peut, en première approximation à basse résolution spectrale,
considérer ce spectre comme la superposition du spectre de 2 corps noirs, dont
on cherche à déterminer les températures.
On note
est l'albédo.
On peut, en première approximation à basse résolution spectrale,
considérer ce spectre comme la superposition du spectre de 2 corps noirs, dont
on cherche à déterminer les températures.
On note 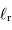 la composante énergétique directement
réfléchie, et
la composante énergétique directement
réfléchie, et 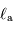 la composante absorbée puis rerayonnée.
la composante absorbée puis rerayonnée.
Question 1)
Montrer que la puissance interceptée par la planète vaut :
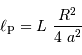
où 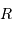 représente le rayon planétaire.
représente le rayon planétaire.
Faire un schéma, et estimer la surface interceptée par la planète
Question 2)
Calculer le rapport 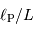 dans le cas de Jupiter et de la Terre.
dans le cas de Jupiter et de la Terre.
| Objet | 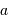 (UA) (UA) | 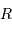 (km) (km) |
| Jupiter | 5.2 | 71000 |
| Terre | 1 | 6400 |
Pour mémoire 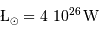 .
.
Question 4)
Quelle est la température 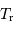 associée au rayonnement réfléchi
associée au rayonnement réfléchi 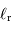 , assimilé à un rayonnement de corps noir ?
, assimilé à un rayonnement de corps noir ?
Question 5)
Montrer que la température associée à la composante
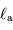 , voisine de la température d'équilibre de la planète, est alors:
, voisine de la température d'équilibre de la planète, est alors:
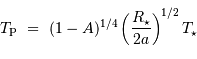
Associer 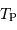 au rayonnement de type corps noir
au rayonnement de type corps noir 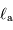 .
.
Question 7)
En déduire la longueur d'onde 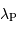 correspondant au maximum de l'émission planétaire.
A quel domaine spectral cette température correspond-elle?
correspondant au maximum de l'émission planétaire.
A quel domaine spectral cette température correspond-elle?
- Question 1
Aide :
Faire un schéma, et estimer la surface interceptée par la planète
Solution :
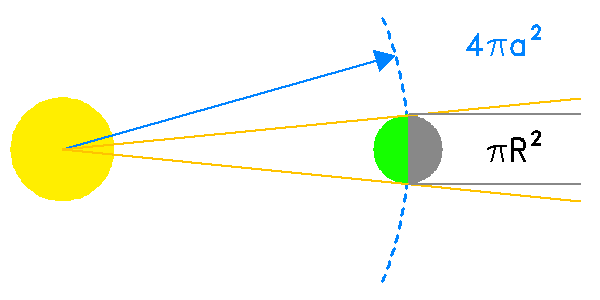
Au niveau de la planète, le flux stellaire est dilué sur une sphère de surface
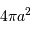 .
La section occultée par la planète, avec
.
La section occultée par la planète, avec 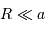 , correspond à celle d'un disque de surface
, correspond à celle d'un disque de surface 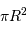 .
.
Le rapport de ces 2 aires vaut :
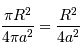
d'où le résultat proposé.
Avec l'hypothèse
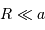
, la surface interceptée par la planète est voisine de
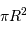
.
Crédit :
ASM
- Question 2
Aide :
Calculette !
Solution :
Les applications numériques donnent :
| Objet | 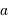 (UA) (UA) | 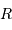 (km) (km) | 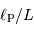 |
| Jupiter | 5.2 | 71000 | 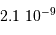 |
| Terre | 1 | 6400 | 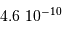 |
- Question 3
Aide :
L'énergie se conserve !
Solution :
La conservation de l'énergie impose
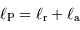
Toute l'énergie reçue sera rerayonnée, soit directement, soit après thermalisation. D'après la définition de l'albédo, il s'ensuit le partage :
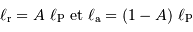
- Question 4
Aide :
Aucun calcul à mener !
Solution :
Le rayonnement directement réfléchi correspond au rayonnement solaire. Sa température de corps noir est donc 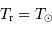 .
.
- Question 5
Aide :
Associer 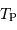 au rayonnement de type corps noir
au rayonnement de type corps noir 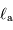 .
.
Solution :
Le rayonnement thermique de la planète correspond, par hypothèse, à un rayonnement de corps noir de température 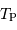 .
.
Il vérifie :
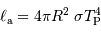
Par ailleurs :
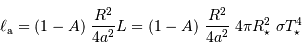
On en déduit :
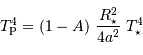
D'où le résultat à démontrer :
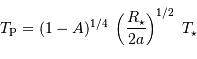
- Question 6
Aide :
Re-calculette !
Solution :
L'application numérique donne environ 1000 K.
- Question 7
Aide :
Aller voir la loi de Wien
Solution :
La loi de Wien donne :
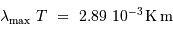
On en déduit que le maximum de rayonnement se situe aux alentours de 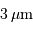 .
.
 Objectifs
Objectifs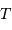 et un rayonnement de corps noir à cette même température.
et un rayonnement de corps noir à cette même température.
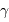 , jusqu'aux photons finalement émis, majoritairement dans les domaines UV, visible et IR.
, jusqu'aux photons finalement émis, majoritairement dans les domaines UV, visible et IR.
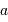 autour de son étoile.
On suppose l'espace interplanétaire vide, ce qui entraîne la conservation du flux stellaire intégrée sur toute surface entourant l'étoile. La rotation propre de la planète est suffisamment rapide pour que l'on puisse
considérer sa température
autour de son étoile.
On suppose l'espace interplanétaire vide, ce qui entraîne la conservation du flux stellaire intégrée sur toute surface entourant l'étoile. La rotation propre de la planète est suffisamment rapide pour que l'on puisse
considérer sa température 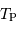 comme uniforme sur toute la surface. On néglige toute autre source
d'énergie que stellaire.
comme uniforme sur toute la surface. On néglige toute autre source
d'énergie que stellaire.
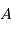 du rayonnement solaire, et en
absorbe une fraction
du rayonnement solaire, et en
absorbe une fraction 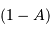 , où
, où 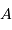 est l'albédo.
On peut, en première approximation à basse résolution spectrale,
considérer ce spectre comme la superposition du spectre de 2 corps noirs, dont
on cherche à déterminer les températures.
On note
est l'albédo.
On peut, en première approximation à basse résolution spectrale,
considérer ce spectre comme la superposition du spectre de 2 corps noirs, dont
on cherche à déterminer les températures.
On note 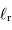 la composante énergétique directement
réfléchie, et
la composante énergétique directement
réfléchie, et 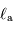 la composante absorbée puis rerayonnée.
la composante absorbée puis rerayonnée.
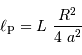
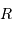 représente le rayon planétaire.
représente le rayon planétaire.
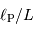 dans le cas de Jupiter et de la Terre.
dans le cas de Jupiter et de la Terre.
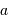 (UA)
(UA) 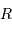 (km)
(km)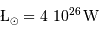 .
.
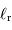 et
et 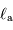 en fonction de la luminosité totale
en fonction de la luminosité totale
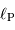 et de l'albédo
et de l'albédo 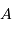 .
.
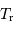 associée au rayonnement réfléchi
associée au rayonnement réfléchi 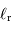 , assimilé à un rayonnement de corps noir ?
, assimilé à un rayonnement de corps noir ?
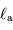 , voisine de la température d'équilibre de la planète, est alors:
, voisine de la température d'équilibre de la planète, est alors:
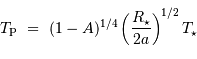
 au rayonnement de type corps noir
au rayonnement de type corps noir  .
.
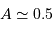 et un demi-grand axe
et un demi-grand axe
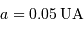 . Pour l'étoile, on prendra :
. Pour l'étoile, on prendra : 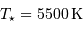 et
et 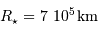 .
.
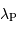 correspondant au maximum de l'émission planétaire.
A quel domaine spectral cette température correspond-elle?
correspondant au maximum de l'émission planétaire.
A quel domaine spectral cette température correspond-elle?
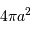 .
La section occultée par la planète, avec
.
La section occultée par la planète, avec 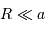 , correspond à celle d'un disque de surface
, correspond à celle d'un disque de surface 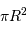 .
.
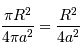

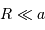 , la surface interceptée par la planète est voisine de
, la surface interceptée par la planète est voisine de 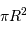 .
.
 (UA)
(UA)  (km)
(km)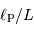
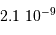
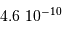
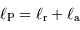
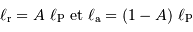
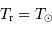 .
.
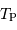 .
.
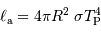
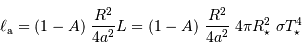
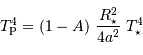
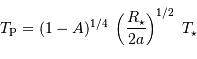
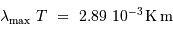
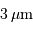 .
.