Introduction à la notion de repère
Auteurs: P. Rocher, Jean-Eudes Arlot
- Introduction
- La voûte céleste
- La sphère locale
- Exercice
- Le mouvement diurne
- Le mouvement annuel
- Les repères, outils mathématiques pour se positionner
- La notion de repère cartésien
- Se positionner dans le plan
- Translation de repère
- Exercice : Calcul de coordonnées polaires dans le plan
- Se positionner dans l'espace
- Exercice : Calcul des coordonnées polaires dans l'espace
- Les unités angulaires
- Exercice : conversion des unités
- Les repères de l'astronomie "fixes"
- Introduction
- Les repères quasi fixes
- Le repère céleste écliptique
- Exercice
- Le repère céleste équatorial
- Changement de repère
- Formulaire de trigonométrie sphérique
- Relations entre les coordonnées polaires écliptiques et équatoriales
- Position du Soleil sur l'écliptique
- Les mouvements du repère équatorial
- La médiation
- Le repère galactique J2000
- Les coordonnées terrestres
- Calcul des coordonnées géocentriques
- Les repères locaux
- Introduction
- Le système de coordonnées équatoriales horaires
- Exercice
- Effet d'un changement de longitude terrestre
- La variation du temps sidéral
- Le repère local
- Quelques définitions supplémentaires
- Formulaires liant les coordonnées locales
- Remarque sur le repère local (alt-azimutal)
- Simulations
- Exercices d'utilisation des simulations
- Applications liées au repère local
- Introduction
- Quelques définitions supplémentaires
- Les astres circumpolaires
- Astres ayant une plus grande digression est et ouest
- Tracer de la sphère locale dans l'hémisphère sud
- Passage au méridien supérieur
- Exercice : Passage au méridien
- Passage d'un astre au méridien inférieur
- Conclusion
- QCM
- Applications liées au repère local-2
- Hauteur du plan équatorial au dessus de l'horizon
- Hauteur du plan équatorial au dessous de l'horizon
- Passage du Soleil au zénith entre les tropiques
- Exercice
- Trouver les limites des étoiles qui ne se lèvent pas
- Trouver les limites des étoiles qui ne se couchent pas
- Trouver les étoiles ayant une plus grande digression
- Distinction entre les étoiles circumpolaires et les étoiles ayant une plus grande digression
- Simulation
- Les nouveaux repères
- Les nouveaux systèmes de reférence
Introduction
 Introduction
Introduction
Comment se repérer dans le ciel ?
Lorsque l'on regarde le ciel depuis le sol terrestre, nous voyons une voûte céleste constellée de points brillants (les étoiles) dont quelques uns en mouvement par rapport aux autres (les planètes), mais nous n'avons pas la sensation de nous mouvoir nous-mêmes dans l'espace. L'idée d'une Terre fixe au centre de l'univers s'impose tout naturellement, mais, à la réflexion, les choses ne sont
pas si simples que cela.

Crédit :
ASM/Gilles Bessou
Tout d'abord nous devons constater que les étoiles et les planètes ne restent pas fixes sur la voûte céleste. Leurs mouvements proviennent, d'une part du mouvement de la Terre autour de son axe (mouvement diurne), d'autre part du mouvement de la Terre autour du Soleil (mouvement apparent annuel du Soleil et des planètes), et enfin du mouvement propre de ces astres (insignifiant pour les étoiles mais régulier et très détectable pour les planètes). L'astronomie de position (ou astrométrie) et la mécanique céleste vont nous aider à déméler tous ces mouvements qui se superposent.
La voûte céleste
La sphère locale
Tout d'abord, notre perception du ciel est celle d'une sphère : étoiles et planètes sont toutes -apparemment- à la même distance de nous. Notre perception du relief, grâce à nos deux yeux, s'arrête en effet, à quelques dizaines de mètres de nous : au-delà, nous ne percevons plus de relief, donc plus de distances mais seulement des angles.
Nous sommes donc, chacun d'entre nous, le centre d'une sphère sur laquelle nous voyons les corps célestes : on l'appelle la sphère céleste locale et on va mesurer des angles sur cette sphère, puis à partir de ces angles et d'un modèle d'univers, on va en déduire la distance de ces points brillants que nous observons.
Dans la sphère céleste locale, on donne la position d'un astre avec deux valeurs, l'angle entre l'astre et l'horizon (mesuré verticalement) et l'angle entre la direction de l'astre et une direction fixe, par exemple le Sud (mesuré horizontalement).
Plus précisément, dans ce repère local, formé du plan de l'horizon et de la direction du Sud, on donne la position de l'astre avec les deux coordonnées :
L'angle azimutal ou azimut : est mesuré dans le plan de l'horizon, de 0 à 360 degrés à partir du Sud, positivement vers l'Ouest. La direction du Sud a donc un azimut de 0°, le point cardinal Ouest a un azimut de +90°, le point cardinal Nord est à +180° et par exemple le Nord-Ouest est à 135° d'azimut. Attention, les géomètres comptent l'azimut à partir du Nord, pas les astronomes !
L'altitude angulaire : c'est la hauteur dans le ciel mesurée de 0° à partir de l'horizon jusqu'à +90° au zénith (le point à la verticale de l'observateur).
Ce repère local dépend de l'observateur et varie d'un point à l'autre sur Terre.
Mais comment s'y retrouver entre observateurs du ciel qui sont à des endroirs différents sur Terre? D'autant plus qu'au-dessus d'un lieu donné, on ne voit pas toujours les mêmes étoiles...
Il faut construire un repère commun à tous les observateurs avec un plan origine, l'équateur (on comprendra plus tard pourquoi ce nom) et un méridien d'origine. Pour cela il y a plusieurs façons d'aborder le problème.
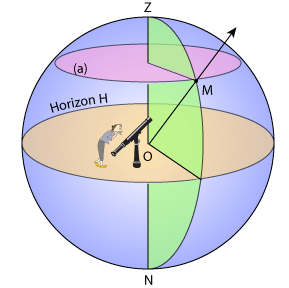
La sphère céleste locale définie par le plan horizontal (H, l'horizon du lieu) et le zénith (Z), l'observateur est en O.
Crédit :
ASM/Jean-Eudes Arlot et Damien Guillaume
Exercice
 La sphère céleste
La sphère céleste
Question 1)
Chaque observateur terrestre est entouré de sa sphère céleste locale dont il est le centre. Sa sphère locale est définie par le zénith du lieu, le plan horizontal et la direction Nord-Sud. Comment les observateurs de différents lieux terrestres pourront-ils comparer leurs mesures de position des astres ?
Il faut chercher des directions fixes communes à tous les observateurs. Quelles sont-elles ?
Le mouvement diurne
Pour déterminer un équateur dans le ciel, on remarque tout d'abord que toutes les étoiles semblent tourner sur des petits cercles autour de l'étoile polaire (c'est le mouvement diurne de la Terre). Ainsi, l'équateur terrestre se projette sur la sphère céleste et dessine un équateur céleste aisé à trouver. Ce mouvement amène à définir le repère céleste équatorial. Dans ce repère, tous les corps célestes, sauf la Lune, ont des coordonnées qui ne changent presque pas au cours de la nuit et très peu d'un jour à l'autre.
Le mouvement de rotation de la Terre autour de son axe apparaît donc de cette façon. Il faut donner ici quelques compléments sur le mouvement diurne. C'est le résultat de la rotation de la Terre autour de son axe. Cette rotation, repérée par rapport à une direction fixe (une étoile, par exemple), va durer 23h 56m 4s pour un tour complet (360°). Si on se repère par rapport à la direction du Soleil, il faudra alors 24h pour ramener celui-ci dans la même direction. En effet, durant sa rotation, la Terre s'est déplacée dans son mouvement de révolution autour du Soleil.
Le mouvement annuel
Au cours de l'année, les étoiles restent fixes les unes par rapport aux autres, mais les corps du système solaire, Lune, Soleil, planètes, bougent par rapport aux étoiles dans une bande du ciel autour de l'écliptique. Le plan de l'écliptique sert à définir le repère céleste écliptique.
Les repères, outils mathématiques pour se positionner
Auteur: P. Rocher
La notion de repère cartésien
Nous vivons et nous observons dans un espace à trois dimensions. Toute étude de mouvement dans notre environnement demande de positionner les corps par rapport à un repère de dimension trois. Le but du présent chapitre est de rappeler les notions de repère dans l'espace et les méthodes mathématiques qui permettent de changer de type de repère. On n'abordera pas dans ce chapitre la notion d'espace relativiste qui introduit le temps local comme quatrième dimension.
Vecteur unitaire sur un axe
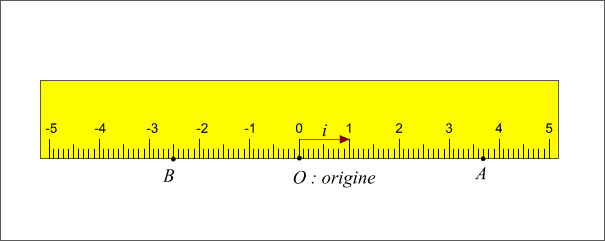
Figure 1: Vecteur unitaire sur un axe.
Crédit :
ASM/Patrick Rocher
On remarquera que nous n'avons pas indiqué d'unité de mesure sur le dessin, l'unité de mesure est la longueur du vecteur 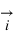 , ce vecteur porte donc le nom de vecteur unitaire.
, ce vecteur porte donc le nom de vecteur unitaire.
On peut également écrire que 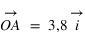 et que
et que 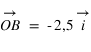 .
.
On remarquera également que chaque point de l'axe a une coordonnée et qu'inversement à chaque coordonnée correspond un point de l'axe. Cette propriété mathématique, appelée bijection entre le droite et l’ensemble des nombres réels, est fondamentale, car c’est elle qui permet de faire de la géométrie analytique.
Nota Bene : En mathématiques, le mot espace n'a pas le sens courant. Le 'plan' courant est un espace à 2 dimensions en mathématique et l''espace' courant est un espace à 3 dimensions en mathématiques. Il n'y a pas de mot courant pour les espaces à 4 (et plus) dimensions.
Se positionner dans le plan
Pour pouvoir se positionner dans le plan, on doit définir un repère ayant la même dimension que le plan : la dimension deux. Pour cela on utilise deux vecteurs unitaires notés 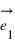 et
et 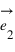 ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
Pour connaître la position d'un point A dans le plan par rapport au repère défini par les deux vecteurs, on va projeter le point A sur l'axe portant le vecteur 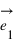 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 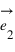 ; et sur l'axe portant le vecteur
; et sur l'axe portant le vecteur 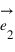 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 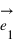 . Les coordonnées
. Les coordonnées 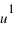 et
et 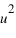 du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire : 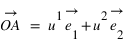 , les coordonnées
, les coordonnées 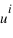 sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).
sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).
Repère quelconque
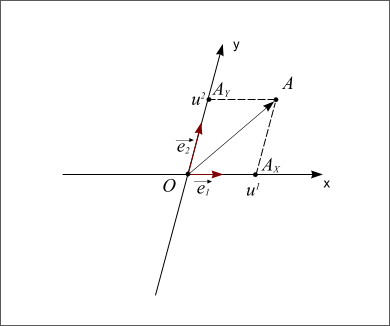
Figure 2: Repère direct quelconque
Crédit :
ASM/Patrick Rocher
Si les deux vecteurs sont perpendiculaires, le repère est dit orthogonal. Si les deux vecteurs ont la même longueur, on dit que le repère est normé. Et si les deux vecteurs sont perpendiculaires et s'ils ont la même longueur alors le repère est dit orthonormé. L'axe Ox porte le nom d'axe des abscisses et l'axe Oy porte le nom d'axe des ordonnées. Enfin si l'on passe de l'axe Ox à l'axe Oy par une rotation dans le sens inverse des aiguilles d'une montre (sens trigonométrique ou sens direct) on dit que le repère est direct. Dans le cas inverse, le repère est dit indirect.
Repère normé
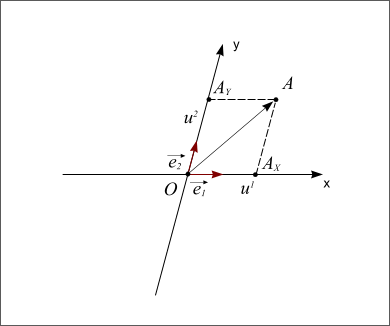
Figure 3 : Repère normé
Crédit :
ASM/Patrick Rocher
Repère orthonormé
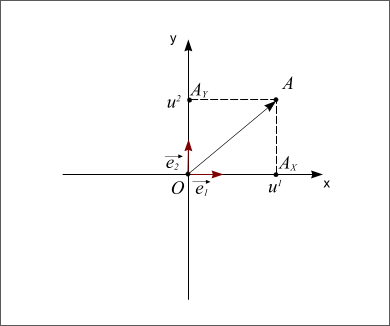
Figure 4 : Repère orthonormé
Crédit :
ASM/Patrick Rocher
Translation de repère
Changement d’origine d’un repère
L'usage de repère cartésien est très répandu, on l'utilise systématiquement lorsque l'on trace un graphique. Il est souvent intéressant de pouvoir déplacer le repère sans pour autant changer l'orientation de ses deux axes. On dit alors que le repère est en translation. Pour un point quelconque du plan, on distingue deux possibilités :
- Le point A est lié au repère, dans ce cas la position du point A dans le repère translaté est la même.
- Le point A n'est pas lié au repère, dans ce cas le point A ne se déplace pas avec le repère et ses coordonnées dans le repère translaté ne sont plus les mêmes.
Figure 5 : Point A lié au repère translaté
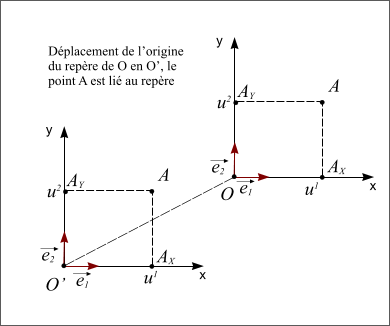
Figure 5 : Point A lié au repère translaté.
Crédit :
ASM/Patrick Rocher
Figure 6 : Point A non lié au repère tranlaté.
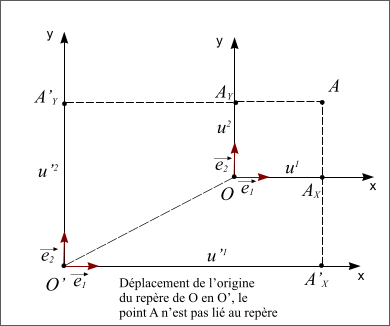
Figure 6 : Point A non lié au repère translaté.
Crédit :
ASM/Patrick Rocher
Rotation de repère
On peut également faire tourner le repère autour de son origine O, dans ce cas on peut également distinguer les points liés au repère qui vont tourner avec lui (dans ce cas leurs coordonnées ne changeront pas) et les points non liés au repère qui ne tourneront pas avec lui (dans ce cas leurs coordonnées vont changer).
Exercice : Calcul de coordonnées polaires dans le plan
Auteur: P. Rocher
 Calcul de coordonnées polaires
Calcul de coordonnées polaires
Soit un point A dans un repère orthonormé dont les coordonnées cartésiennes sont 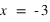 et
et 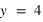 .
.
Question 1)
Calculer les coordonnées polaires de ce point , l'angle sera donné en degrés ?
Utiliser les formules du cours, attention aux unités pour l'angle si vous utilisez votre calculette.
Se positionner dans l'espace
Coordonnées cartésiennes
Pour se positionner dans l’espace, il convient d’ajouter une troisième dimension. Tout ce que nous avons dit pour les repères à deux dimensions se transpose pour les repères à trois dimensions.
La figure suivante représente un repère orthonormé direct, le troisième axe est l’axe Oz.
Repère orthonormé direct
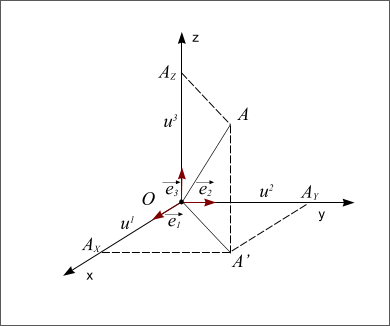
Figure 7 : Repère orthonormé direct.
Crédit :
ASM/Patrick Rocherr
Le point A est projeté orthogonalement en A’ sur le plan Oxy, puis A’ est projeté en AX sur l’axe Ox et en AY sur l’axe Oy. Le point A est également projeté orthogonalement en AZ sur l’axe Oz. Les coordonnées 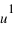 ,
,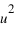 et
et 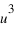 du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire : 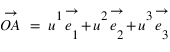 , les coordonnées
, les coordonnées 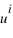 sont appelées coordonnées contravariantes du vecteur
sont appelées coordonnées contravariantes du vecteur 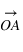 (ou projections parallèles). Elles sont souvent notées (x,y,z).
(ou projections parallèles). Elles sont souvent notées (x,y,z).
Exercice : Calcul des coordonnées polaires dans l'espace
Auteur: P. Rocher
 Calcul de coordonnées polaires
Calcul de coordonnées polaires
Difficulté : ☆☆☆
Question 1)
Le 18 janvier les coordonnées cartésiennes géocentriques de la Lune sont les suivantes : 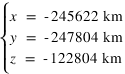 Calculer les coordonnées polaires (θ,φ,r) correspondantes, on donnera les valeurs des angles en degré, minute et seconde d'angle.
Calculer les coordonnées polaires (θ,φ,r) correspondantes, on donnera les valeurs des angles en degré, minute et seconde d'angle.
On fera attention aux signes de x et de y pour déterminer le bon angle φ.
Les unités angulaires
Le poids des traditions est très fort dans nos cultures, la standardisation des unités de mesure n’est pas toujours suivie d’effet et l’on trouve encore en fonction des pays et des publications des usages non standards. Ainsi les Anglo-saxons utilisent le mille terrestre international plus souvent que le mètre et les cartographes français utilisent encore le grade pour mesure les longitudes et les latitudes terrestres !
Les angles plans sont mesurés avec quatre systèmes d’unités :
Le radian
Le radian. La mesure d’un angle en utilisant cette unité se fait en radian et en fraction décimale de radian. C’est l’unité que l’on doit utiliser dans les calculs, en effet lorsque l'on dérive ou intègre une fonction trigonométrique l’angle doit être exprimé en radian.
Le degré sexagésimal
Le degré sexagésimal Cette unité est très ancienne, elle est basée sur le système sexagésimal qui permettait de faire des divisions facilement à l’époque où l’on connaissait mal les fractions. Le degré se divise en 60 minutes (symbole : ′), la minute se divise en 60 secondes (symbole : ″) etc. Dans le passé on divisait la seconde en 60 tierces (symbole : ′″) qui était elle-même divisée en 60 quatrièmes (symbole : IV). De nos jours on utilise plus les divisions inférieures à la seconde (on utilise les fractions décimales de la seconde), mais vous trouverez les anciennes notations dans les livres anciens. On remarquera que les symboles (′ - ″ - ′″ - IV ) correspondent à la numérotation romaine (I, II, III, IV) mise en exposant.
L'heure sexagésimale
L’heure sexagésimale L’heure se divise en 60 minutes (symbole : min), la minute se divise en 60 secondes (symbole : s). Il n’y a pas de divisions inférieures à la seconde (on utilise les fractions décimales de la seconde). Cette unité est encore largement utilisée en astronomie. Attention c’est une unité angulaire et non une unité de temps. L’unité de temps est définie à partir de la définition de la seconde de temps.
Le grade centésimal
Le grade centésimal Ce système est centésimal, ainsi le grade se divise en 100 minutes (symbole : ′) centésimales, la minute centésimale se divise en 100 secondes centésimales (symbole : ″) etc. On retrouve ici l’avantage du système centésimal, 23gr 35′ 25″ est égale à 23,3525 gr et si l’on prend le quadrant (angle droit) comme unité 0,233525 est directement le rapport de l’angle à l’angle droit.
On a les relations suivantes entre les différentes unités : 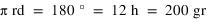
Exercice : conversion des unités
Auteur: P. Rocher
 Conversion des unités
Conversion des unités
Question 1)
Convertir un radian dans les différentes autres unités.
On donnera les valeurs trouvées en utilisant les subdivisions de chaque unités (par exemple h,min et secnde).
Les repères de l'astronomie "fixes"
Introduction
Nous allons décrire les repères astronomiques classiques. Ces dernières années, l’amélioration croissante de la précision des observations a nécessité des réformes importantes et la création de nouveaux repères célestes et terrestres que nous aborderons que très succinctement dans les pages « pour en savoir plus ».
Les repères quasi fixes
Historiquement, deux plans fondamentaux se sont imposés. Le premier est le plan de l’orbite apparente du Soleil vue depuis la Terre. Plus rigoureusement, il s'agit du plan de l'orbite du barycentre Terre-Lune. Ce plan est appelé écliptique, car c’est lorsque la Lune est proche de ce plan qu’il y a possibilité d’éclipse. Le Soleil, la Lune et les planètes sont toujours très proches de ce plan. Ce repère écliptique est utilisé pour étudier les mouvements des objets du système solaire.'
L’autre plan est le plan de l’équateur terrestre. Ce repère, le repère céleste équatorial est le repère principal pour les astrophysiciens (terriens!). Dans ce repère, les étoiles ont des coordonnées fixes.
Les astronomes ont construit un repère fondamental avec chacun de ces plans. Comme ces plans ne sont pas totalement fixes, ces repères sont définis pour un instant donné, par exemple pour l’instant correspondant au 1er janvier 2000 à 12h que l’on nomme époque J2000. De plus comme l’astronome observe et mesure uniquement des angles, on se limite souvent à des coordonnées polaires sur une sphère de rayon unité appelée sphère céleste.
Le repère céleste écliptique
Le repère écliptique J2000 est défini par le plan de base (Oxy) correspondant à l’orbite osculatricedu barycentre Terre-Lune autour du Soleil, la direction de l’axe Oz normale à ce plan (appelée pôle de l’écliptique) est choisie de sorte que le mouvement du barycentre Terre-Lune se fasse dans le sens direct (sens inverse des aiguilles d’une montre). Dans ce repère les coordonnées portent le nom de coordonnées écliptiques J2000. Les deux coordonnées polaires sont respectivement la longitude écliptique et la latitude écliptique. La longitude (notée 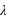 ) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée
) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée 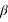 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.
Repère écliptique
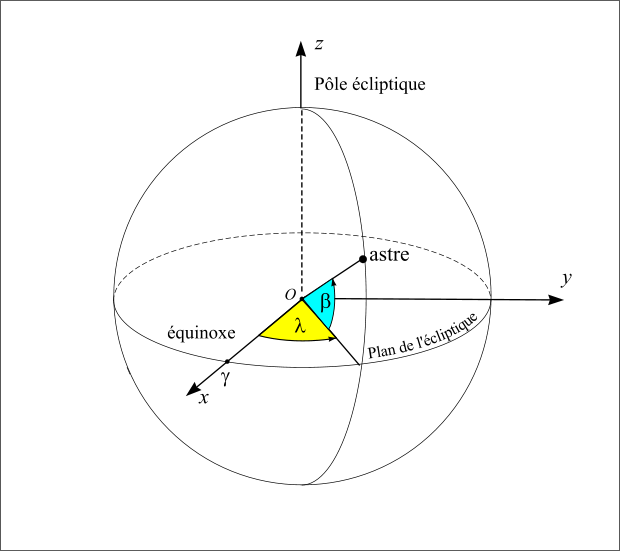
Figure 8 : Repère écliptique.
Crédit :
ASM/Patrick Rocher
Exercice
 Le repère écliptique
Le repère écliptique
Question 1)
Sachant que toutes les planètes se trouvent, comme le Soleil, dans l'écliptique ou très proches de l'écliptique, quelles sont, dans l’hémisphère nord, les meilleures conditions pour observer les planètes extérieures (Mars, Jupiter, Saturne, Uranus et Neptune) au plus haut dans le ciel nocturne ?
Dans l'hémisphère nord le Soleil culmine dans le ciel le jour du solstice d'été et il est au plus bas le jour du solstice d'hiver.
Ne pas oublier que le Soleil est toujours dans l'écliptique été comme hiver et que l'écliptique est toujours visible dans le ciel jour et nuit.
Le repère céleste équatorial
Le repère céleste équatorial
Le repère équatorial J2000 est défini par le plan de base (Oxy) correspondant au plan de l’équateur céleste (plan parallèle à l’équateur terrestre passant par le centre du repère) à l’instant considéré, la direction de l’axe Oz normale à ce plan (appelée pôle céleste nord) est choisie de sorte que le mouvement de la Terre autour de cet axe se fasse dans le sens direct (sens inverse des aiguilles d’une montre – donc d’ouest en est). Dans ce repère les coordonnées portent le nom de coordonnées équatoriales J2000. Les deux coordonnées polaires sont respectivement l’ascension droite et la déclinaison. L’ascension droite (notée 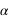 ) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée
) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée 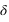 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée 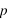 ).
).
Repère céleste équatorial
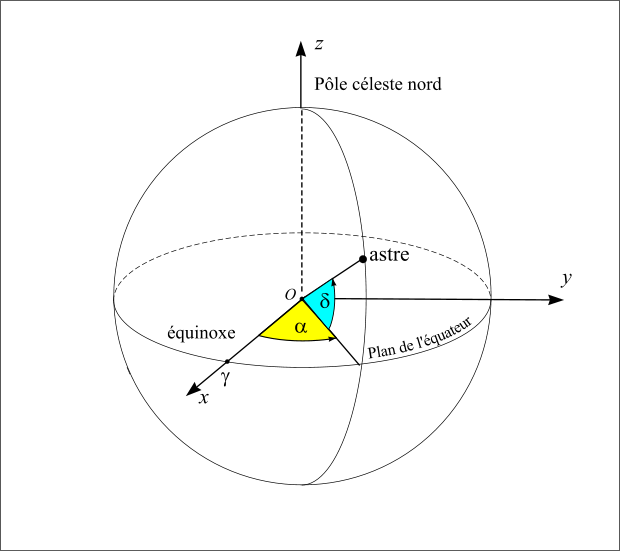
Figure 9 : Repère céleste équatorial.
Crédit :
ASM/Patrick Rocher
 Remarques
Remarques
On remarquera que nous n’avons pas encore précisé les directions origines Ox du repère écliptique et du repère équatorial. On pourrait définir des origines quelconques pour ces deux repères, mais comme l’axe de rotation de la Terre n’est pas perpendiculaire à son orbite, le plan de l’équateur n’est pas parallèle au plan de l’écliptique. L’intersection de ces deux plans est une droite que l’on nomme droite des équinoxes. Il était donc judicieux d’utiliser cette droite commune pour définir un axe Ox commun aux deux repères. Sur cette droite, on a le choix entre deux directions pour orienter l’axe Ox, on a choisi la direction de l’équinoxe correspondant au passage du Soleil des déclinaisons négatives aux déclinaisons positives dans son mouvement apparent annuel autour de la Terre. Cet équinoxe est appelé l’équinoxe de printemps ou point vernal. Il est noté pour la lettre gamma Υ, lettre grecque proche du symboledu signe du Bélier. La direction opposée est appelée direction de l’équinoxe d’automne, elle est notée par la lettre grecque oméga majuscule Ω proche du symbole du signe de la Balance.
Attention la direction de l’équinoxe de printemps est unique, elle ne change pas en fonction de l’hémisphère terrestre où l’on se trouve comme on le lit parfois. C’est le début de la saison astronomique qui change. Dans l’hémisphère nord le printemps commence lorsque le Soleil passe par l’équinoxe de printemps, cet instant correspond au début de l’automne dans l’hémisphère sud.
Changement de repère
Changement de repère
Les deux repères ayant le même axe Ox, on passe d’un repère à l’autre en faisant une rotation autour de cet axe Ox. Cet angle est l’angle que fait l’écliptique céleste avec l’équateur céleste. Il porte de nom d’obliquité de l’écliptique et est noté ε. Sa valeur à l’époque J2000 est proche de 23° 26' 21". Cet angle est également l’angle que fait l’axe de rotation de la Terre avec la normale à l’écliptique (pôle de l’écliptique).
Les deux repères (écliptique et équatorial).
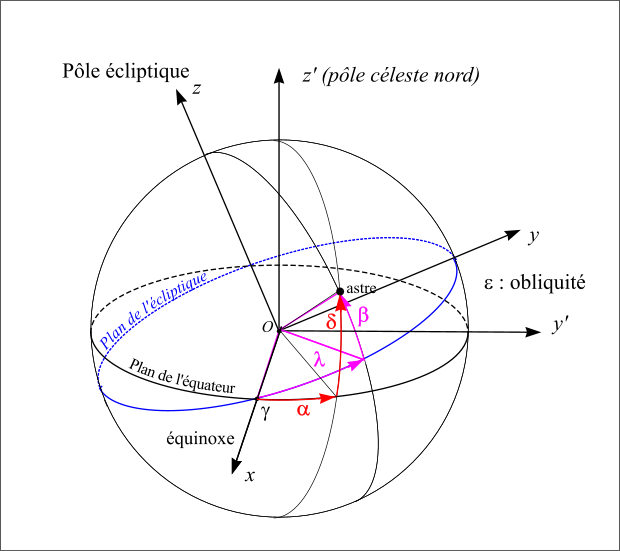
Figure 10 : Les deux repères (écliptique et équateur).
Crédit :
ASM/Patrick Rocher
Nouvelles définitions
Le grand cercle de la sphère céleste passant par les pôles célestes et les équinoxes porte le nom de colure des équinoxes. La droite perpendiculaire à la droite des équinoxes contenue dans le plan de l’écliptique porte le nom de droite des solstices. De même le grand cercle de la sphère céleste qui passe par les pôles célestes et les points solsticiaux porte le nom de colure des solstices. On remarquera que le colure des solstices passe également par les pôles de l’écliptique. Les colures des solstices et des équinoxes divisent l’équateur et l’écliptique en quatre secteurs égaux de 90°.
Selon l’origine des repères on parlera de :
- coordonnées barycentriques si l’origine est au barycentre du système solaire,
- coordonnées héliocentriques si l’origine est au centre de masse du Soleil,
- coordonnées géocentriques si l’origine est au centre de masse de la Terre,
- coordonnées topocentriques si l’origine est un lieu à la surface terrestre,
- coordonnées sélénocentriques si l’origine est au centre de masse de la Lune.
Formulaire de trigonométrie sphérique
Les formulaires de changement de repères en coordonnées polaires font appel à la trigonométrie sphérique.
Pour cela nous allons utiliser les formules de trigonométriques sphériques classiques.
Triangle sphérique
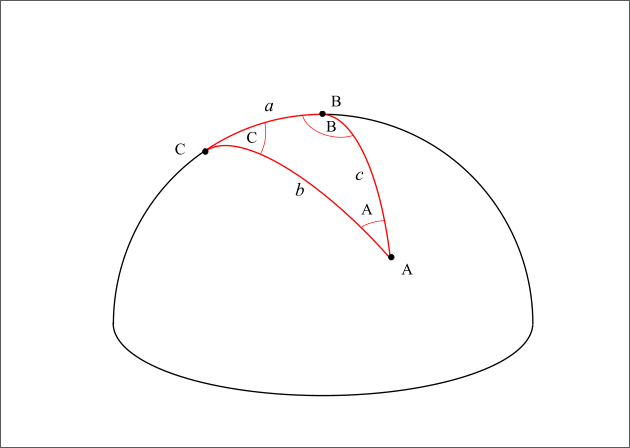
Figure 11 : Triangle sphérique.
Crédit :
ASM/Patrick Rocher
Considérons un triangle sphérique ABC formé par des arcs de grands cercles de la sphère, ce triangle possède trois angles aux sommets A, B et C et trois angles « côtés » a, b, c. A, B et C sont les angles entre les arcs de grands cercles et a, b et c sont les longueurs angulaires des arcs de grands cercles. Entre ces six angles, on a les relations trigonométriques suivantes :
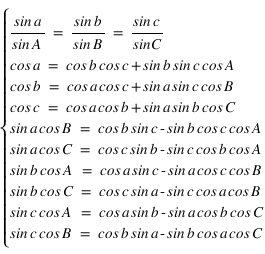
Il est inutile de connaître ces formules par cœur, il suffit de savoir qu’elles existent et de s’y rapporter lorsque l’on a un calcul à faire.
Relations entre les coordonnées polaires écliptiques et équatoriales
Si l’on trace les deux repères sur la sphère céleste et un astre quelconque en A, le pôle de l’écliptique PE, le pôle nord céleste P et la direction de l’astre A forme un triangle sphérique (PEPA).
Triangle sphérique, repères écliptique et équatorial.
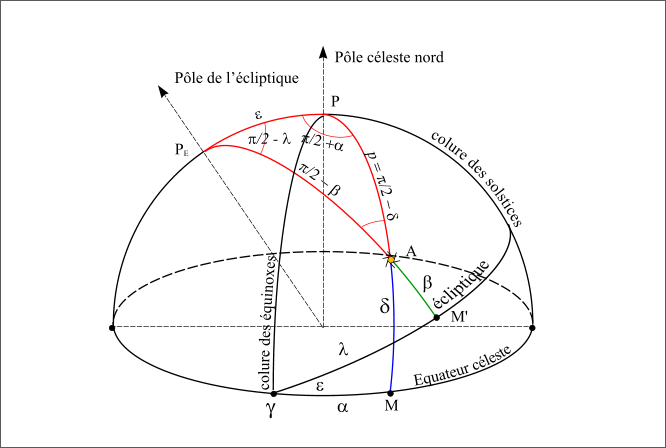
Figure 12 : Triangle sphérique, repères écliptique et équatorial.
Crédit :
ASM/Patrick Rocher
Dans ce triangle on connait cinq des six angles :
- L’arc PEP est l’obliquité ε,
- L’arc PEA est le complémentaire de la latitude écliptique :
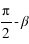 ,
, - L’arc PA est la distance polaire ou le complémentaire de la déclinaison :
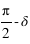 ,
, - L’angle entre l’arc PEP et l’arc PEA est le complémentaire de la longitude écliptique :
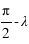 ,
, - L’angle entre PEP et PA est égal à 90° (π/2) l’angle entre les deux colures plus l’ascension droite de l’astre :
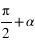 .
.
Pour avoir par exemple les coordonnées équatoriales en fonction des coordonnées écliptiques, il suffit d’écrire les relations suivantes :
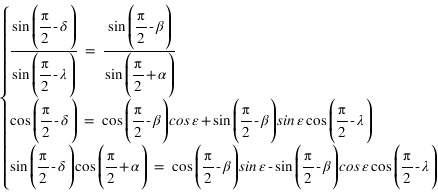
Ce qui donne après simplification :
Système (1) 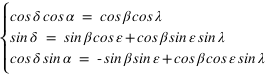
La déclinaison s’obtient à l’aide de la seconde relation en prenant l’arc sinus de sin δ (car δ est compris en –90° et +90°) l’ascension droite est obtenue grâce à la première et à la troisième relation. La connaissance du sinus et du cosinus de l’ascension droite permet de connaître l’ascension droite sur l’intervalle allant de 0° à 360°. On doit ensuite mettre ces deux variables dans le bon système d’unités (heures sexagésimales pour l’ascension droite et degrés sexagésimaux pour la déclinaison).
On a des relations identiques pour passer des coordonnées équatoriales aux coordonnées écliptiques.
Système (2) 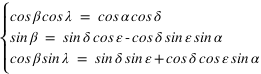
Auteur: ASM/Patrick Rocher
 Calcul des coordonnées équatoriales du Soleil
Calcul des coordonnées équatoriales du Soleil
Cet exercice a pour but de vous faire calculer les coordonnées équatoriales du Soleil à partir de ces coordonnées écliptiques.
Pour simplifier, le calcul on supposera que la latitude du Soleil β est nulle, ce qui implique que 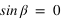 et que
et que 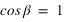 . Le système (1) est donc simplifié.
. Le système (1) est donc simplifié.
Question 1)
Le 1 janvier 2012 à 0h UTC, la longitude apparente λ du Soleil est de 279° 57' 30", calculer son ascension droite et sa déclinaison sachant que l'obliquité de l'écliptique ε à cet instant est de 23°26' 12,7". On exprimera l'ascension droite en heures, minutes et secondes d'angle et la déclinaison en dégres, minutes et secondes d'angle.
Le système (1) lorsque l'on prend une latitude nulle à la forme simplifier suivante : 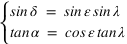 .
Faites attention aux unités, la calculatrice en ligne utilise des radians !
.
Faites attention aux unités, la calculatrice en ligne utilise des radians !
Position du Soleil sur l'écliptique
Position du Soleil sur l'écliptique 
Cette simulation a pour but de vous montrer le mouvement du Soleil apparent sur l'écliptique.
Elle montre l'inclinaison de l'écliptique sur l'équateur céleste (noté ε), la longitude écliptique du Soleil apparent et les coordonnées équatoriales (ascension droite α et déclinaison δ). P est le pôle Nord céleste et K est le pôle Nord de l'écliptique.
Dans cette simulation, la latitude du Soleil est supposée nulle, en réalité la latitude du Soleil est très faible et varie en fonction du temps. Cet écart provient du fait que l'écliptique est construit à partir du mouvement du barycentre Terre-Lune alors que les coordonnées du Soleil sont calculées depuis le centre de la Terre.
Remarques
Les coordonnées équatoriales du Soleil variant peu au court d'une journée, on peut utiliser cet applet pour calculer les coordonnées équatoriales du Soleil un jour donné.
On vérifiera deux choses importantes :
Auteur: P. Rocher
 Variation journalière de la longitude et de l'ascension droite du Soleil
Variation journalière de la longitude et de l'ascension droite du Soleil
Question 1)
Placez-vous le 5 janvier 2012, noter la longitude. Avancez d'un jour est refaite la même mesure. En déduire la variation journalière en longitude. Refaites la même mesure pour le 5 et le 6 juillet 2012. Que peut-on en déduire?
Question 2)
Le jour de l'équinoxe de printemps est le jour où la longitude du Soleil passe par 0°, celui de l'équinoxe d'automne est celui où la longitude du Soleil est égale à 180°. Les jours des solstices d'été et d'hiver correspondent respectivement au jour où la longitude du Soleil passe par 90° et 270°. Calculez les dates des saisons pour une année donnée.
Les mouvements du repère équatorial
En fait la direction de l’axe instantané de rotation de la Terre n’est pas constante. Historiquement le mouvement de cet axe a été décomposé en deux parties : une composante circulaire appelée précession et une composante formée de multiples variations périodiques appelée nutation. La composante circulaire fait parcourir à l’axe de rotation de la Terre un cône dans le sens rétrograde à la vitesse d’environ 50″ par an (un tour en environ 26000 ans). Cette précession se traduit par un mouvement de l’axe des équinoxes à la même vitesse également dans le sens rétrograde (appeler précession des équinoxes). On peut donc définir des repères écliptiques et équatoriaux dans lesquels on corrige de la précession, pour une date donnée, la position de l’équinoxe. Dans ce cas les repères sont dits moyens de la date.
On peut aussi définir des repères écliptiques et équatoriaux dans lesquels on corrige, pour une date donnée, la position de l’équinoxe de la précession et de la nutation (qui agit également sur l’obliquité de l’écliptique). Dans ce cas les repères sont dits vrais de la date.
On voit l’importance de la connaissance du mouvement de l’axe de rotation de la Terre.
On voit également que le repère écliptique dépend de la théorie du barycentre Terre-Lune et que l’usage d’une origine tournante, la direction de l’équinoxe n’est forcément judicieuse, car elle varie en fonction de la théorie de la précession utilisée.
Précession des équinoxes
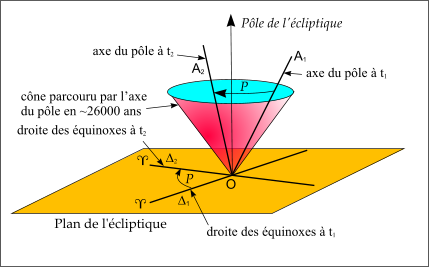
Figure 13 : Précession des équinoxes.
Crédit :
ASM/Patrick Rocher
La médiation
La médiation est une notation hybride basée sur les deux repères écliptique et équatorial. Considérons le cercle horaire portant l’astre A. Ce cercle horaire coupe l’équateur céleste en H et il coupe l’écliptique en MA que l’on nomme point de médiation de l’astre A. On appelle médiation de l’astre A l’arc 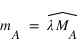 , sa longitude écliptique étant λ , M étant la projection de la direction de l’astre sur l’écliptique.
, sa longitude écliptique étant λ , M étant la projection de la direction de l’astre sur l’écliptique.
Parfois on donne le couple de coordonnées formé par la médiation et la déclinaison à la place des coordonnées équatoriales classiques (ascension droite et déclinaison). Ce couple de coordonnées n’est pas orthogonal, mais il est parfois utilisé notamment dans les instruments anciens (astrolabe).
La médiation d'un astre.
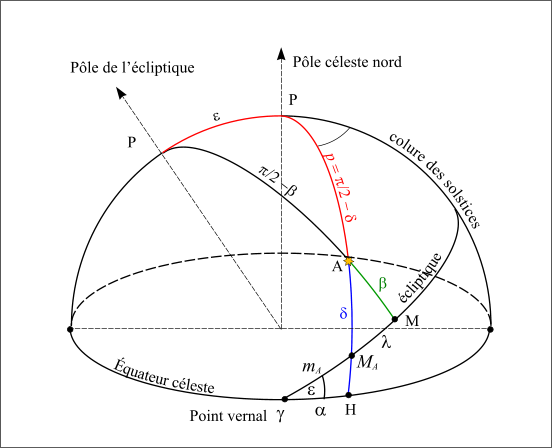
Figure 14 : La médiation d'un astre.
Crédit :
ASM/Patrick Rocher
Le repère galactique J2000
Les astronomes utilisent également un repère particulier pour positionner les étoiles par rapport au plan de notre galaxie : le repère galactique.
Le repère galactique
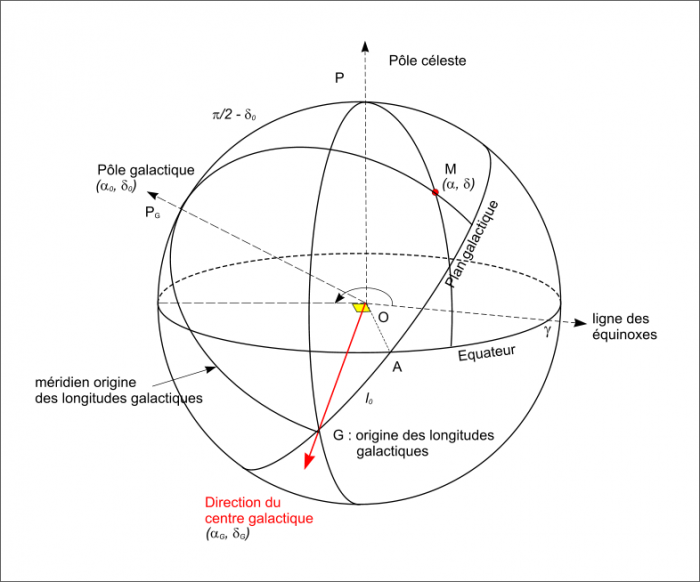
Figure 15 : Le repère galactique.
Crédit :
ASM/Patrick Rocher
Soit PG (α0, δ0) la direction du pôle galactique dans le repère équatorial J2000 et OG (αG, δG) la direction du centre galactique dans ce même repère. Les coordonnées géocentriques galactiques J2000, la longitude et latitude galactiques sont définies dans le repère direct construit à l’aide du plan galactique et le pôle galactique. Le méridien origine des longitudes étant défini par la direction du centre galactique. Nous noterons l0 l’angle AG (positif dans le sens rétrograde). L’ascension droite αA du point A est égale α0 + π/2 et l’inclinaison i du plan galactique sur l’équateur est égale à α0 – π/2. Le plan galactique ainsi défini est le plan passant par le centre de la Terre, normal à la direction du pôle galactique. Ce repère est un repère géocentrique J2000, car il est défini par rapport au repère fixe équatorial J2000.
Les coordonnées terrestres
Les coordonnées terrestres sont données par rapport au pôle terrestre et le plan de l’équateur terrestre. Ce système constitue un référentiel terrestre. Les coordonnées polaires terrestres portent les noms de latitude (notée φ) et longitude (notée L) terrestres. L’axe instantané de rotation de la Terre se déplace par rapport aux étoiles, mais il reste quasi fixe par rapport à la croûte terrestre.
Par contre la Terre n’étant pas parfaitement sphérique (elle est aplatie aux pôles), on doit distinguer deux types de coordonnées : des coordonnées géographiques (ou astronomiques) et des coordonnées géocentriques.
En première approximation la Terre est assimilée à un ellipsoïde de révolution.
Un méridien terrestre est un arc de longitude constante joignant les deux pôles terrestres.
Sur cet ellipsoïde on définit un méridien origine passant par les deux pôles géographiques. Ce méridien origine porte le nom de méridien international (méridien de Greenwich). Pour un lieu donné, on distingue une seule longitude et deux latitudes :
- la latitude géocentrique φ' qui est l’angle entre la direction allant du centre de la Terre au lieu considéré et le plan de l’équateur terrestre,
- la latitude géographique ou astronomique φ qui est l’angle entre la normale à l’ellipsoïde de référence et le plan de l’équateur terrestre.
coordonnées géographiques
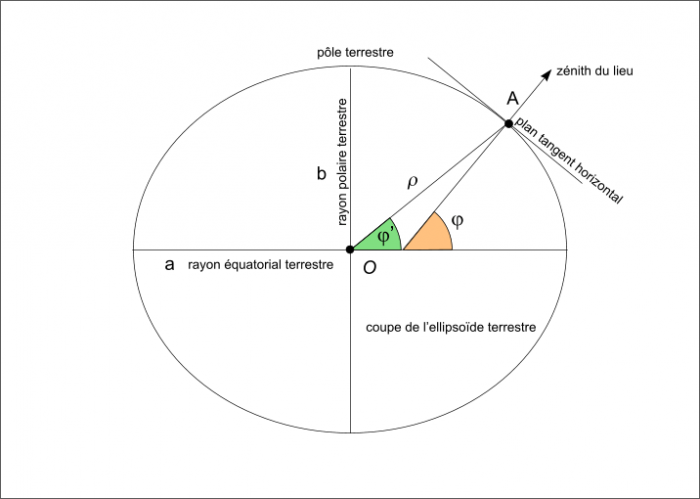
Figure 16 : Coordonnées géographiques.
Crédit :
ASM/Patrick Rocher
Historiquement les latitudes géographiques étaient obtenues à l’aide de mesures de hauteur d’astre aux dessus de l’horizon.
La longitude est comptée à partir du méridien international en heures ou en degrés sexagésimaux. Historiquement les longitudes géographiques étaient obtenues à l’aide de mesures astronomiques (point astronomique).
De nos jours les coordonnées géographiques sont obtenues à l’aide de systèmes satellitaires (GPS).
Sur une planète on parlera de coordonnées planétographiques et de coordonnées planétocentriques.
Calcul des coordonnées géocentriques
Soit φ la latitude géographique, φ' la latitude géocentrique et h l’altitude du lieu.
a est le rayon équatorial terrestre et f est l’aplatissement de l’ellipsoïde terrestre.
ρ est la distance entre le centre de la Terre et le lieu exprimé en rayon terrestre équatorial.
On a les relations suivantes :
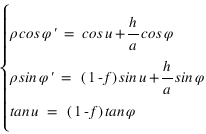
La connaissance des quantités 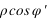 et
et 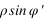 est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
Quelques ellipsoïdes de références
| Système géodésique | Ellipsoïde associé | aen mètres | b en mètres | f |
|---|
| NTF | Clarke 1880 IGN | 6378249,2 | 6356515,0 | 1/293,466021 |
| ED50 | ED50 Hayford 1909 | 6378388,0 | 6356911,9461 | 1/297,000000 |
| WGS84 et RGF 83 | IAG GRS 1980 | 6378137,0 | 6356752,314 | 1/298,257222 |
Auteur: P. Rocher
 Calcul de la latitude géocentrique de Paris
Calcul de la latitude géocentrique de Paris
Les coordonnées géographiques de l'Observatoire de Paris sont les suivantes :Latitude géographique : 48° 50' 11,2" N, longitude géographique : 2° 20' 13,8" E, altitude : 67m.
Question 1)
Calculer les coordonnées géocentriques de l’Observatoire de Paris en utilisant le système géodésique WGS84.
On calculera d'abord la valeur de u, puis les valeurs de 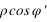 et
et 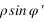 .
.
Les repères locaux
Auteur: Patrick Rocher
Introduction
Les deux repères écliptique et équatorial sont fixes pour une époque donnée, même centrés au centre de la Terre, ils ne tiennent pas compte du mouvement de l’observateur, ni de sa position. Nous allons décrire deux nouveaux repères qui vont être liés à un observateur sur la Terre. Ces repère vont donc tourner avec notre planète. Nous devons donc, dans un premier temps, exprimer la rotation de la Terre par rapport au répère équatorial terrestre.
Le système de coordonnées équatoriales horaires
Le temps sidéral
Ce système est un système intermédiaire dans lequel le repère équatorial est lié à la Terre, c’est-à-dire qu’il tourne avec elle. Il est caractérisé par un méridien origine (le méridien du lieu) et un angle qui donne la position du point vernal (direction de l’équinoxe de printemps) par rapport à ce méridien. Cet angle s’appelle le temps sidéral local (noté TL). Cet angle est exprimé en heures sexagésimales, il est compté positivement vers l’ouest (sens des aiguilles d’une montre) à partir du méridien local. Ainsi l’angle temps sidéral local croît avec le temps.
Le temps sidéral local à Greenwich
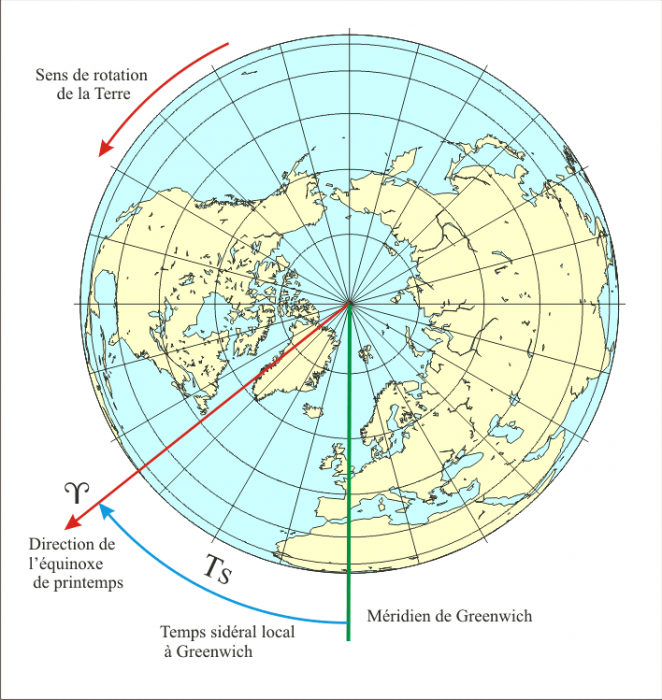
Figure 17 : Le temps sidéral local.
Crédit :
ASM/Patrick Rocher
Les coordonnées équatoriales horaires
Le système de coordonnées équatoriales horaires est un système polaire dont le plan de base (Oxy) est l’équateur céleste, Ox est la direction du méridien local, Oy est dans le sens indirect (90° vers l’ouest) et Oz est l’axe du pôle céleste. Le premier angle est l’angle horaire (noté H), compté positivement en heures sexagésimales de 0h à 24h vers l’ouest à partir du méridien du lieu, le second angle est la déclinaison (le même angle que celui du repère équatorial). L’angle horaire, comme le temps sidéral, croît avec le temps.
Les petits cercles parallèles à l’équateur portent le nom de parallèles célestes et les demi-grands cercles joignant les pôles célestes portent le nom de cercles horaires. Tous les astres qui ont une déclinaison constante décrivent dans le mouvement diurne un parallèle céleste. En particulier, l'étoile Polaire décrit actuellement un petit cercle dont le rayon est inférieur à 1° autour du pôle céleste, ce qui nous permet de situer le pôle céleste à un degré près. Cela n’a pas toujours été le cas. Ainsi au XIIIe siècle d’étoile polaire était à 4° du pôle céleste cela en raison de la précession des équinoxes.
Repère équatorial horaire
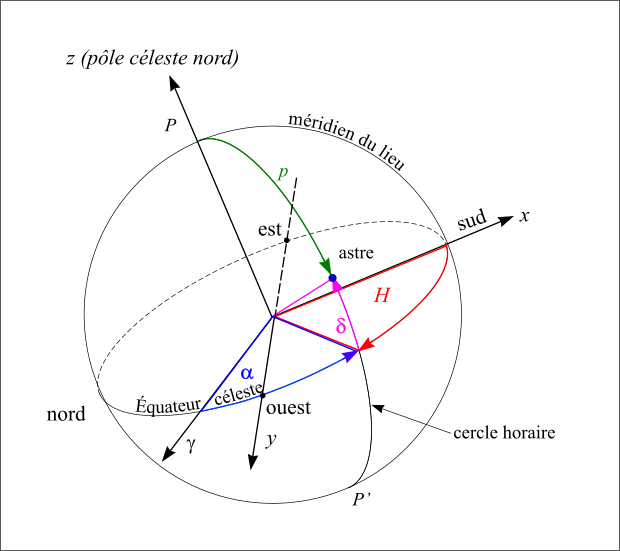
Figure 18 : Repère équatorial local.
Crédit :
ASM/Patrick Rocher
On a une relation simple entre l’ascension droite, l’angle horaire et le temps sidéral local :
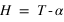
Attention dans les formules ces angles doivent être dans le même système d’unités.
On remarquera que l’angle horaire d’un astre est le même pour tous les lieux situés sur un même méridien terrestre.
Compte tenu de la définition de l’angle horaire, le temps sidéral local est l’angle horaire du point vernal.
Exercice
 Le temps sidéral
Le temps sidéral
Question 1)
Quelle est l'ascension droite α d'une étoile passant au méridien d'un lieu donné à un instant donné ?
Quelle est la valeur de l'angle horaire d'un astre qui passe au méridien? Quelle est la formule fondamentale liant l'ascension droite et l'angle horaire?
Effet d'un changement de longitude terrestre
Si l’on change de méridien, à un instant donné, le temps sidéral local du nouveau méridien est égal au temps sidéral de l’ancien méridien augmenté de la différence de longitude si le nouveau méridien est à l’est de l’ancien ou diminué de la différence de longitude si le nouveau méridien est à l’ouest de l’ancien. Attention les longitudes doivent être dans le même système d’unités que le temps sidéral (généralement en heures sexagésimales). Attention également aux conventions pour la notation des longitudes : dans le passé les longitudes étaient comptées négativement vers l’est (de 0° à -180° ou 0h à -12h) et positivement vers l’ouest (de 0° à 180° ou 0h 12h) à partir du méridien de Greenwich. La formule donnant le temps sidéral local TL en un lieu de longitude L par rapport au temps sidéral à Greenwich TG était donc :
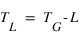
De nos jours les conventions sur la longitude ont changé, la longitude est comptée positivement vers l’est à partir du méridien de Greenwich de 0° à 360° (ou de 0h à 24h) la formule précédente se transforme donc en :
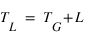
On trouve donc les deux formules dans la littérature et cela est la source de nombreuses erreurs de calcul. Pour les éviter, il suffit de se souvenir que le temps sidéral croît par rapport à Greenwich lorsque la longitude est vers l’est et décroit lorsque la longitude est vers l’ouest. N’oubliez pas non plus que certaines cartes donnent la longitude par rapport au méridien de Paris en grade !
La variation du temps sidéral
Le temps sidéral est l’angle horaire de la direction de l’équinoxe de printemps (le point gamma), il varie (en moyenne) de 24h (ou 360°) en 23h 56min 4s de temps moyen.
Cela permet de calculer le temps sidéral local en tout point de la Terre à un instant t à partir de la connaissance du temps sidéral au méridien de Greenwich à 0h. Le calcul se fait en deux étapes : on calcule le temps sidéral à Greenwich à l’instant t, puis le temps sidéral au lieu considéré en ajoutant ou en retranchant la longitude du lieu.
Relations entre la variation du temps moyen 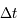 et la variation
et la variation 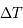 du temps sidéral :
du temps sidéral :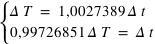
Nous sommes capables de construire une horloge de temps sidéral local. Sur ces horloges, l’aiguille des heures fait deux tours en 23h 56min 4s de notre échelle de temps. La connaissance du temps sidéral est importante, car elle permet de calculer l’angle horaire d’un astre (angle qu’il fait avec la direction du sud, lorsque l’on connaît son ascension droite. Inversement lorsque l’on connait le temps sidéral local d’un événement on peut en déduire :
- le temps moyen de l’événement si on connaît la longitude du lieu,
- la longitude du lieu si l’on connaît le temps moyen de l’événement.
Remarque : Comme ce repère local ne dépend que de la longitude, on peut le placer au centre de la Terre ou sur un lieu quelconque situé sur le méridien. Nous verrons que ce changement d’origine modifie la valeur des coordonnées pour des astres proches (parallaxe diurne).
Auteur: P. Rocher
 Calcul du temps sidéral local en un lieu donné
Calcul du temps sidéral local en un lieu donné
Difficulté : ☆☆☆
Question 1)
Déterminer le temps sidéral local à Paris le 30 mars 2010 à 18h 3m 42s UTC (l’heure UTC est le temps moyen de Greenwich) à Paris (longitude : 9min 21s est). Le temps sidéral à Greenwich à 0hUTC étant de 12h 29min 7s.
Faire une règle de trois en sachant qu'en 23h 56min 4s de temps moyen le temps sidéral varie de 24h ou utiliser directement les formules de conversions.
Le repère local
En un lieu donné, de latitude géographique φ et de longitude géographique L on peut définir un repère local dont le plan Oxy est par le plan horizontal tangent à l’ellipsoïde au lieu considéré et dont l’axe Oz est la normale à ce plan (direction du zénith). Comme dans le cas des coordonnées horaires, l’axe Ox est l’intersection du plan du méridien et du plan horizontal (direction du sud) et l’axe Oy est à 90° compté vers l’ouest dans le sens indirect (direction de l’ouest). On appelle premier vertical ouest le demi-plan vertical passant par la verticale du lieu et la direction de l’ouest. On définit de même le premier vertical est comme le demi-plan vertical passant par la direction de l’est.
Le premier angle est compté positivement à partir du sud vers l’ouest (sens indirect – sens des aiguilles d’une montre) de 0° à 360° et s’appelle l’azimut des astronomes (noté a). On a donc les relations suivantes :
sud ⇔ azimut = 0°, ouest ⇔ azimut = 90°, nord ⇔ azimut = 180° et est ⇔ azimut = 270°. La direction de la vertical, vers le haut, d'un lieu porte le nom de zénith, sa direction opposée, vers le bas, porte le nom de nadir.
Le second angle est compté positivement vers le zénith de 0° à 90°et négativement vers le nadir de 0° à –90°, il porte le nom de hauteur (noté h). À la place de la hauteur, on utilise parfois l’angle entre la direction du zénith et la direction de l’astre, cet angle est compté de 0° à 180° à partir du zénith et porte de nom de distance zénithale (notée z).
Repère local azimutal
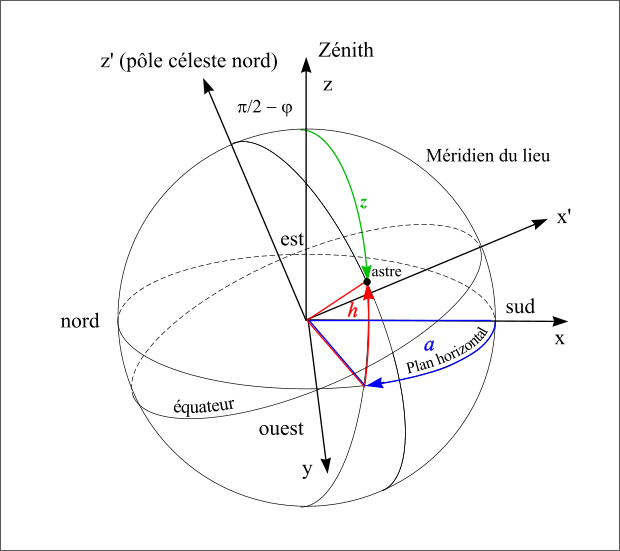
Figure 19 : Repère local azimutal.
Crédit :
ASM/Patrick Rocher
Quelques définitions supplémentaires
Lors du lever d’un astre, sa hauteur apparente est nulle (h = 0), on donne parfois l’angle entre la direction de l’est et la direction de l’astre à son lever, cet angle porte le nom d’amplitude ortive. De même lors du coucher d’un astre, on donne parfois l’angle entre la direction de l’ouest et la direction de l’astre à son coucher, cet angle porte le nom d’amplitude occase.
Enfin les cercles de hauteurs égales, petits cercles de la sphère céleste parallèles à l’horizon, portent le nom almicantarat.
Pour un lieu de l’hémisphère nord, l’angle entre le zénith et le pôle céleste nord est égal au complémentaire de la latitude du lieu (π/2 – φ). Le complémentaire de la latitude porte le nom de colatitude.
C’est aussi l’angle entre le plan équatorial céleste et le plan horizontal.
Formulaires liant les coordonnées locales
Le triangle sphérique construit avec le pôle céleste nord, le zénith du lieu et la direction d’un astre est le suivant :
triangle-local
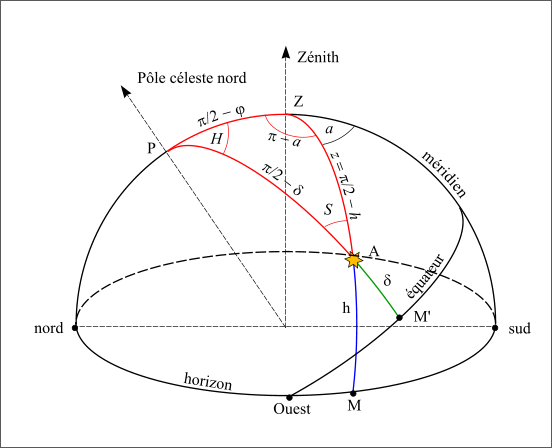
Figure 20 : Triangle sphèrique local.
Crédit :
ASM/Patrick Rocher
En utilisant les relations de trigonométrie sphérique sur les cinq angles connus, on démontre les relations suivantes :
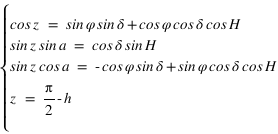
et inversement
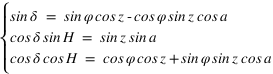
Le sixième angle, formé par les directions du zénith et du pôle céleste vues depuis l’astre porte le nom d’angle à l’astre (noté S).
Remarque sur le repère local (alt-azimutal)
Les géographes et les marins utilisent un azimut compté également dans le sens indirect, mais à partir du nord. L’azimut d’un astre pour un lieu de l’hémisphère nord croît avec le temps ainsi le Soleil se déplace d’est en ouest en passant vers le sud.
Inversement dans l’hémisphère sud l’azimut décroit avec le temps, ainsi le Soleil se déplace d’est en ouest en passant vers le nord.
Les montres ayant été inventées dans l’hémisphère nord, les aiguilles de la montre suivent le mouvement de l’ombre des cadrans solaires de l’hémisphère nord donc est-sud-ouest.
Dans l’hémisphère nord la hauteur du pôle céleste est égale à la latitude du lieu (en fait ce n’est pas tout à fait vrai en raison de la réfraction atmosphérique).
Simulations
Pour bien comprendre les systèmes de coordonnées, on peut utiliser les simulations suivantes.
 Coordonnées équatoriales et horizontales
Coordonnées équatoriales et horizontales
Coordonnées équatoriales et horizontales 
La première simulation affiche la position d'un astre sur la sphère céleste, en coordonnées équatoriales (α, δ) et en coordonnées horizontales (a, h). On y voit aussi le point vernal γ et l'angle horaire H. Z est le zénith et P est le pôle céleste.
Les paramètres de la simulation sont les suivants :
- Coordonnées équatoriales de l'astre, ascension droite α et déclinaison δ ;
- position sur Terre, latitude φ et longitude L ;
- date et heure en temps universel.
En bas de la simulation, on trouve les données calculées à partir des paramètres : angle horaire H, hauteur h et azimut a.
On peut trouver les coordonnées et le fuseau horaire d'une ville sur le web.
 Position du Soleil sur l'écliptique
Position du Soleil sur l'écliptique
Position du Soleil sur l'écliptique 
La deuxième simulation montre la position du Soleil sur l'écliptique à une date donnée. Cette simulation montre l'inclinaison de l'écliptique par rapport à l'équateur ε, la longitude écliptique λ, l'ascension droite α et la déclinaison δ. P est le pôle Nord céleste et K est le pôle Nord de l'écliptique. Les quantités calculées par rapport à la date et affichées en bas sont λ, α et δ.
Les coordonnées équatoriales du Soleil variant peu au court d'une journée, on peut les obtenir à partir de cette simulation pour une date donnée, et les utiliser dans la première simulation pour voir la position du Soleil en coordonnées horizontales pendant la journée.
Exercices d'utilisation des simulations
Auteur: Damien Guillaume
 Visibilité des étoiles
Visibilité des étoiles
Difficulté : ☆☆
Cet exercice propose d'utiliser l'applet Coordonnées équatoriales et horizontales pour déterminer la visibilité d'étoiles en différents endroits sur Terre.
Données
- Sirius : ascension droite α = 6h 45m, déclinaison δ = -16° 43'
- Dubhe : α = 11h 04m, δ = +61° 45'
- France (Paris) : latitude φ = +49°, longitude L = 2° E, fuseau horaire = UTC+1
- Afrique du Sud (Cape Town) : φ = -34°, L = 18° E, UTC+2
- Japon (Tokyo) : φ = 36° N, L = 140° E, UTC+9
Question 1)
A l'aide de l'applet, trouver les mois de l'année où Sirius est visible à minuit en France (à Paris), en Afrique du Sud (Cape Town) et au Japon (Tokyo).
Attention au décalage horaire !
Pour simplifier, on pourra prendre minuit heure locale sans tenir compte des différences heures d'été / heures d'hiver.
Par convention, la longitude est positive vers l'Est. Donc 140° E = +140°.
Question 2)
Même question pour l'étoile Dubhe (α UMa).
Question 3)
Expliquer les résultats.
Applications liées au repère local
Auteur: P. Rocher
Introduction
Tout ce que nous observons depuis la Terre se fait dans le repère local. Habitant dans l'hémisphère nord, nous sommes habitués à voir un ciel et des phénomènes liés à notre hémisphère. Nous allons dans les rubriques suivantes décrire des phénomènes pour un lieu quelconque de la Terre.
Quelques définitions supplémentaires
Un demi-cercle de la sphère céleste joignant le zénith au nadir porte le nom de demi-cercle d’égal azimut.
Le demi-cercle de la sphère céleste joignant le pôle céleste nord au pôle céleste sud et contenant le zénith porte le nom de méridien supérieur, par définition tous les points de ce demi-cercle ont un angle horaire nul (H = 0h = 0°), ce demi-cercle est toujours l’origine des angles horaires.
Le demi-cercle de la sphère céleste joignant le pôle céleste nord au pôle céleste sud et contenant le nadir porte le nom de méridien inférieur, par définition tous les points de ce demi-cercle ont un angle horaire de 12h (H = 12h = 180°).
Le demi-cercle d’égal azimut contenant le pôle céleste sud est souvent appelé méridien sud, c’est un abus de langage on devrait parler de demi-cercle d’azimut nul (a = 0°) ou d’azimut sud, ce demi-cercle est toujours l’origine des azimuts.
Le demi-cercle d’égal azimut contenant le pôle céleste nord est souvent appelé méridien nord, c’est également un abus de langage on devrait parler de demi-cercle d’azimut 180° (a = 180°) ou d’azimut nord.
Les astres circumpolaires
Suite à la rotation de la Terre autour de son axe, tous les astres passent au méridien inférieur et au méridien supérieur.
- Si les deux passages sont observables, l’astre est dit circumpolaire, il ne se couche pas.
- Si les deux passages sont inobservables, l’astre ne se lève pas.
- Si seul le passage supérieur est observable, l’astre se lève et se couche.
Par observable on entend que le passage serait visible en absence de Soleil c’est-à-dire qu’il n’aurait pas lieu sous l’horizon.
Astres circumpolaires
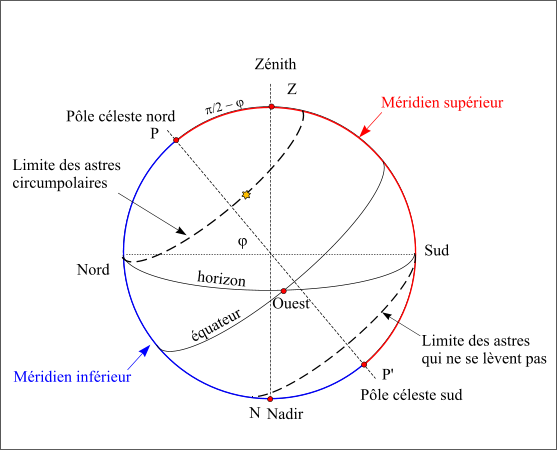
Figure 21 : Astres circumpolaires.
Crédit :
ASM/Patrick Rocher
Astres ayant une plus grande digression est et ouest
Par contre, tous les astres ne passent pas tous au méridien nord et au méridien sud, en effet certains astres passent deux fois dans le méridien nord (a = 180°) ou deux fois dans le méridien sud (a = 0°). Pour un lieu de l’hémisphère nord, ce sont les astres qui passent entre le zénith et le pôle céleste nord (observable) ou entre le nadir et le pôle céleste sud (inobservable, car toujours sous l’horizon). Comme l’azimut ne varie plus de 0° à 360°, il présente deux valeurs extrêmes (une entre 0° et 180° et l’autre entre 180° et 360°). C’est deux valeurs extrêmes correspondent aux plus grandes digressions ouest et est de l’astre.
Plus grande digression d'un astre.
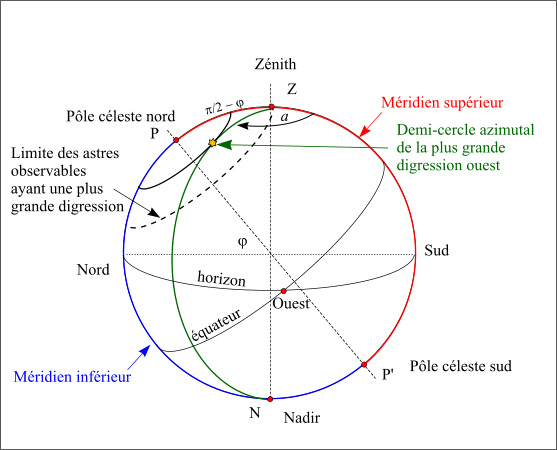
Figure 22 : Plus grande digression d'un astre.
Crédit :
ASM/Patrick Rocher
Tracer de la sphère locale dans l'hémisphère sud
On voit très souvent une représentation de la sphère céleste locale pour un lieu de l’hémisphère nord, il est intéressant de tracer également la sphère céleste locale pour un lieu de l’hémisphère sud.
Sphère locale dans l'hémisphère nord
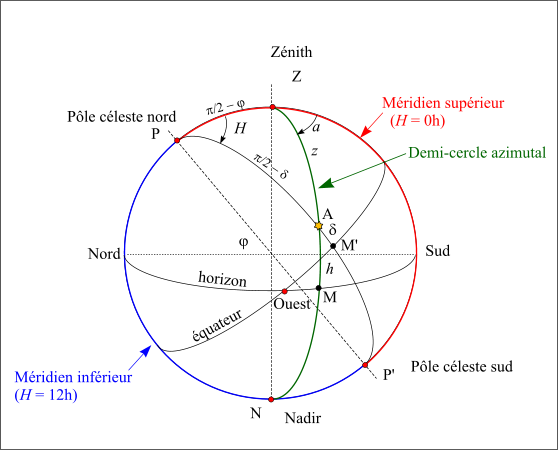
La sphère locale dans l'hémisphère nord.
Crédit :
ASM/Patrick Rocher
La sphère locale dans l'hémisphère sud
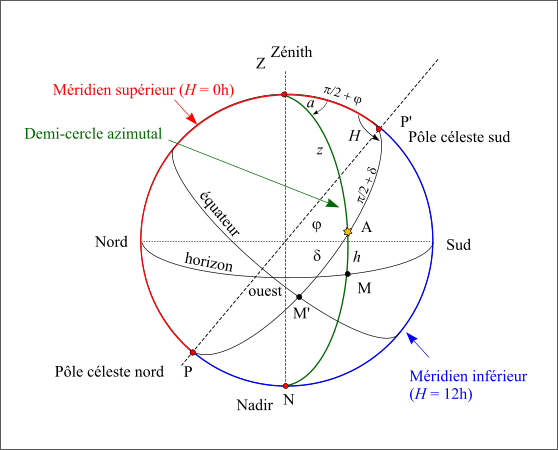
La sphère locale dans l'hémisphère sud.
Crédit :
ASM/Patrick Rocher
On remarque bien que l’angle horaire H d’un astre est croissant avec le temps que l’on soit dans l’hémisphère nord ou dans l’hémisphère sud, par contre l’azimut de l’astre (a) décroit avec le temps dans l’hémisphère sud alors qu’il croît avec le temps dans l’hémisphère nord. Ce choix de variables croissantes avec le temps est volontaire, il s'oppose à la logique mathématique qui favorise des repères directs.
Passage au méridien supérieur
Il y a deux méthodes pour étudier les conditions d’un passage au méridien supérieur, soit faire des dessins de chaque cas de figure en fonction de la latitude du lieu et déterminer les résultats par des raisonnements purement géométriques, soit utiliser une méthode analytique en regardant les résultats sur l’azimut obtenus en fixant la valeur de l’angle horaire lorsque l’astre est dans le méridien. C'est cette seconde méthode que nous allons utiliser.
Les équations ci-dessous montrent qu'on a alors deux solutions :
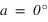 et
et 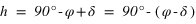 équation (1)
équation (1)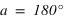 et
et 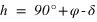 équation (2)
équation (2)
Avec la condition supplémentaire liée à la définition de la hauteur : 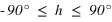 .
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si
.
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si 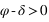 donc si
donc si 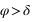 . Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si
. Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si 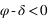 donc si
donc si 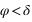 . Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors
. Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors 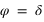 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.
Passage au méridien supérieur.
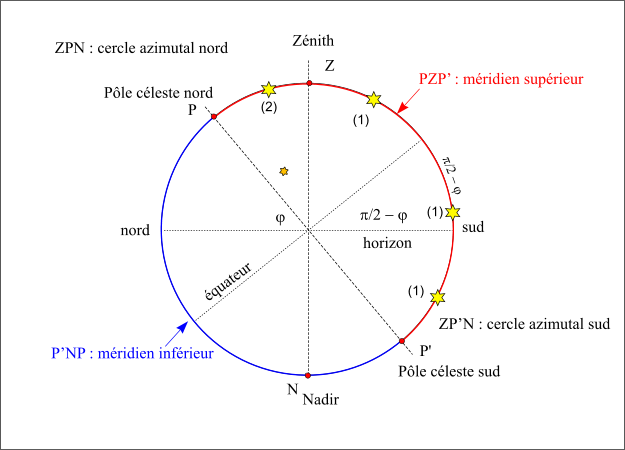
Figure 24 : Passage au méridien supérieur.
Crédit :
ASM/Patrick Rocher
Sur la figure, on a fait une coupe méridienne de la sphère céleste. Le méridien supérieur est représenté en rouge c’est le demi-cercle PZP’. L’étoile notée (2) passe au méridien supérieur avec un azimut nord (elle est sur l’arc ZPN), sa hauteur est comptée à partir de la direction nord de l’horizon.
Les autres étoiles, notées (1), passent au méridien supérieur avec un azimut sud (elles sont sur l’arc ZP’N) leurs hauteurs sont comptées à partir de la direction sud de l’horizon ; deux passent au-dessus de l’horizon, la troisième passe sous l’horizon, car une partie du méridien supérieur est sous l’horizon (sud-P’).
On remarquera aussi que la médiation de l’astre correspond à la longitude de l’écliptique qui passe au méridien en même temps que l’astre.
Exercice : Passage au méridien
Auteur: P. Rocher
 Passage du Soleil au méridien
Passage du Soleil au méridien
Difficulté : ☆☆☆
La déclinaison du Soleil varie au cours de l’année de –23° 26' 21" (au solstice d’hiver) à 23° 26' 21" (au solstice d’été) en passant par 0° (aux équinoxes).
Question 1)
Quelles sont les hauteurs du Soleil à son passage au méridien supérieur à Paris (latitude géographique : 48° 50' 11,2" N) au début de chaque saison astronomique.
On utilisera les deux solutions (1) et (2) avec la condition portant sur la hauteur, pour choisir la bonne solution.
Question 2)
Quelles sont les hauteurs du Soleil à son passage au méridien supérieur au Cap (latitude géographique : 33° 56' 0,0" S) au début de chaque saison.
Question 3)
Quelle est la latitude des lieux où le Soleil passe au zénith le jour du solstice d’été ? Quel est le nom de ce parallèle terrestre ?
Question 4)
Quelle est la latitude des lieux où le Soleil passe au zénith le jour du solstice d’hiver ? Quel est le nom de ce parallèle terrestre ?
Question 5)
Quelle est la latitude des lieux où le Soleil passe au zénith le jour des équinoxes ? Quel est le nom de ce parallèle terrestre ?
Passage d'un astre au méridien inférieur
Par définition, à l'instant du passage au méridien inférieur, l'angle horaire est égale à 180° (H = 180°).
Les équations ci-dessous montrent qu'on a donc deux solutions :
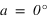 et
et 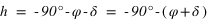 équation (3)
équation (3)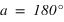 et
et 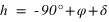 équation (4)
équation (4)
Avec toujours la condition supplémentaire : 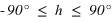 . On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si
. On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si 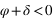 donc si
donc si 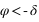 . Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si
. Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si 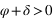 donc si
donc si 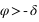 . Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors
. Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors 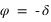 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.
Passage au méridien inférieur
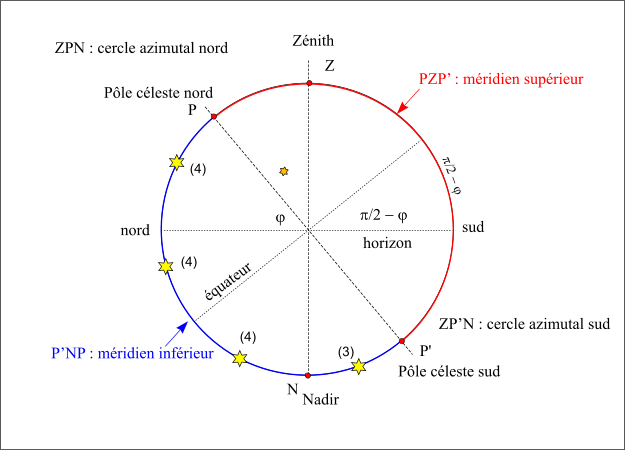
Figure 25 : Passage au méridien inférieur.
Crédit :
ASM/Patrick Rocher
Sur la figure, on a fait une coupe méridienne de la sphère céleste. Le méridien inférieur est représenté en bleu c’est le demi-cercle PNP’. L’étoile notée (3) passe au méridien inférieur avec un azimut nord (elle est sur l’arc ZP’N), sa hauteur est comptée à partir de la direction sud de l’horizon.
Les autres étoiles, notées (4), passent au méridien inférieur avec un azimut nord (elles sont sur l’arc ZPN) leurs hauteurs sont comptées à partir de la direction nord de l’horizon ; une passe au dessus de l’horizon, car une partie du méridien inférieur est au-dessus de l’horizon (nord -P), les deux autres passent sous l’horizon.
Conclusion
QCM
Applications liées au repère local-2
Auteur: Patrick Rocher
Hauteur du plan équatorial au dessus de l'horizon
Pour connaître l'angle entre le plan équatorial et le plan horizontal, on doit calculer l’intersection entre le plan équatorial et le méridien supérieur du lieu. Ce qui se traduit par une déclinaison nulle (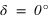 ) et le méridien supérieur => équation (1) ou (2) avec h positif.
) et le méridien supérieur => équation (1) ou (2) avec h positif.
La hauteur h obtenue avec l’équation (1) est positive (comprise entre 0° et 90°) si la latitude φ est comprise entre 0° et 90° donc dans l’hémisphère nord, la hauteur h de l’équateur sur l’horizon est égale à 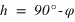 (colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
(colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
La hauteur h obtenue avec l’équation (2) est positive ou nulle (comprise entre 0° et 90°) si la latitude φ est comprise entre –90° et 0° donc dans l’hémisphère sud, la hauteur h de l’équateur sur l’horizon est égale à 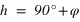 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie donc que la hauteur de l’équateur est bien le complémentaire de la latitude du lieu si le complémentaire est égal à 90° moins la valeur absolue de la latitude. De même la hauteur du pôle au-dessous de l’horizon, qui est le complémentaire de cet angle est égale à la valeur absolue de la latitude.
 Calcul de la hauteur de l'équateur
Calcul de la hauteur de l'équateur
Question 1)
Calculer la hauteur de l’équateur au méridien à Paris (latitude géographique : 48° 50' 11,2" N) et au Cap (latitude géographique : 33° 56' 0,0" S).
Hauteur du plan équatorial au dessous de l'horizon
Pour connaître l'angle entre l’équateur et le plan horizontal, on doit calculer l’intersection entre le plan équatorial et le méridien inférieur du lieu. Ce qui se traduit par une déclinaison nulle (φ = 0°) et le méridien inférieur => équation (3) ou (4) avec h négatif.
La hauteur h obtenue avec l’équation (3) est négative et comprise entre –90° et 0° si la latitude δ est comprise entre –90° et 0° donc dans l’hémisphère sud, la hauteur h de l’équateur sous l’horizon est égale à 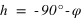 et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
La hauteur h obtenue avec l’équation (4) est négative et comprise entre -90° et 0° si la latitude δ est comprise entre 0° et 90° donc dans l’hémisphère nord, la hauteur h de l’équateur sous l’horizon est égale à 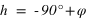 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
 Calcul de la hauteur du plan équatorial sous l'horizon
Calcul de la hauteur du plan équatorial sous l'horizon
Question 1)
Calculer la hauteur de l’équateur au dessous de l’horizon au méridien à Paris (latitude géographique : 48° 50' 11,2" N) et au Cap (latitude géographique : 33° 56' 0,0" S).
Passage du Soleil au zénith entre les tropiques
Exercice
 La déclinaison d'une étoile au zénith
La déclinaison d'une étoile au zénith
Question 1)
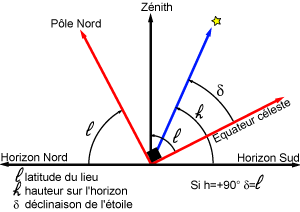
La direction du pôle Nord et l'équateur céleste nous fournissent des directions fixes pour toutes les sphères célestes liées aux observateurs individuels. Dans ce système de repérage, chaque étoile a sa propre déclinaison. Si, à un instant donné on voit une étoile au zénith d'un lieu particulier de latitude 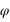 , quelle sera la déclinaison de cette étoile ?
, quelle sera la déclinaison de cette étoile ?
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
C'est la latitude du lieu ! Pourquoi ?
Trouver les limites des étoiles qui ne se lèvent pas
Pour un lieu quelconque de latitude φ, les étoiles qui ne se lèvent pas sont celles dont la hauteur du passage au méridien supérieur est toujours négative ou nulle.
- L’équation (1) donne
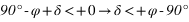
- L’équation (2) donne
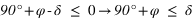
De plus la déclinaison doit toujours être comprise entre –90° et +90° donc la première inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant 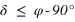 . De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant
. De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant 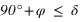 . Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
. Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
Auteur: P.Rocher
 Etoiles sous l'horizon
Etoiles sous l'horizon
Question 1)
À Paris (latitude géographique : 48° 50' 11,2" N) quelles sont les déclinaisons limites des étoiles qui ne se lèvent pas ?
Question 2)
Au Cap, en Afrique du sud (latitude géographique : 33° 56' 0,0" S) quelles sont les déclinaisons limites des étoiles qui ne se lèvent pas ?
Trouver les limites des étoiles qui ne se couchent pas
Pour qu'une étoile ne se couche pas, il faut que sa hauteur au passage au méridien inférieur soit positive ou nulle. On utilise donc les équations (3) et (4).
- L’équation (3) donne
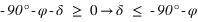
- L’équation (4) donne
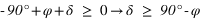
De nouveau, la déclinaison doit toujours être comprise entre –90° et +90° donc la première inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles circumpolaires doivent avoir une déclinaison vérifiant 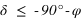 .
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant
.
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant 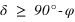 .
.
Cas particuliers : À l’équateur il n’y a aucune étoile circumpolaire. Au pôle Nord toutes les étoiles de déclinaisons positives sont circumpolaires et au pôle Sud toutes les étoiles de déclinaisons négatives sont circumpolaires.
Auteur: P. Rocher
 Exemples d'étoiles circumpolaires
Exemples d'étoiles circumpolaires
Question 1)
À Paris (latitude géographique : 48° 50' 11,2" N) quelles sont les déclinaisons limites des étoiles circumpolaires ?
Question 2)
Au Cap (Afrique du sud) (Latitude géographique : 33° 56' 0,0" S) quelles sont les déclinaisons limites des étoiles circumpolaires ?
Question 3)
Quelle est la latitude des lieux où le Soleil ne couche pas le jour du solstice d’été ? Quel est le nom de ce parallèle terrestre ? Montrer qu’en ces lieux le Soleil ne se lève pas le jour du solstice d’hiver.
Question 4)
Quels sont les lieux sur Terre où l’on voit, au cours de l’année, le plus d’étoiles ?
Question 5)
Quels sont les lieux sur Terre où l’on voit au cours de l’année le moins d’étoiles ?
Trouver les étoiles ayant une plus grande digression
On a vu que les étoiles qui ont une plus grande digression orientale ou occidentale sont les étoiles qui passent au méridien supérieur entre le zénith et le pôle.
Dans l’hémisphère nord : le passage au méridien supérieur doit se faire au nord (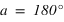 ) donc
) donc 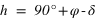 doit être inférieur à 90° donc
doit être inférieur à 90° donc 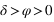 .
.
Dans l’hémisphère sud : le passage au méridien supérieur doit se faire au sud (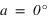 ) donc
) donc 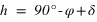 doit être inférieur à 90° donc
doit être inférieur à 90° donc 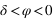 .
.
 Calcul des étoiles ayant une plus grande digression
Calcul des étoiles ayant une plus grande digression
Question 1)
À Paris (latitude géographique : 48° 50' 11,2" N) quelles sont les déclinaisons limites des étoiles qui ont une plus grande digression ?
Question 2)
Au Cap (Afrique du sud) (Latitude géographique : 33° 56' 0,0" S) quelles sont les déclinaisons limites des étoiles qui ont une plus grande digression ?
Distinction entre les étoiles circumpolaires et les étoiles ayant une plus grande digression
Il ne faut confondre étoiles circumpolaires et étoiles présentant une plus grande digression, c’est deux notions ne sont pas identiques. Par exemple dans l’hémisphère nord on a :
- Étoiles circumpolaires ⇔
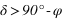 équation (1)
équation (1) - Plus grande digression ⇔
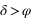 équation (2)
équation (2)
Si la latitude est supérieure à 45° la relation (2) implique (1), donc toutes les étoiles ayant une plus grande digression sont circumpolaires. Par contre, l’inverse n’est pas vrai (1) n’implique pas (2), donc toutes les circumpolaires n’ont pas forcément une plus grande digression. Par exemple pour une latitude de 50° nord, les étoiles ayant une déclinaison de 43° vérifient (1) (43°>40°), mais ne vérifient pas (2) (43°<50°).
Si la latitude est inférieure à 45°, c’est l’inverse : (1) implique (2), donc toutes les étoiles circumpolaires ont une plus grande digression, mais (2) n’implique pas (1) c’est-à-dire que toutes les étoiles ayant une plus grande digression ne sont pas forcément circumpolaires, par exemple pour une latitude de 30°, les étoiles ayant une déclinaison de 40° vérifient (2) (40°>30°), mais ne vérifient pas (1) (40°<60°).
Il y a identité entre les types d’étoiles que pour la latitude 45°.
Simulation
Pour bien comprendre les notions que nous venons de voir, on peut utliser la simulation suivante :
Coordonnées équatoriales et horizontales
Coordonnées équatoriales et horizontales 
Cette simulation affiche la sphère locale et la sphère équatoriale locale pour une latitude géographique φ et une longitude géographique L que l'on peut faire varier.
On peut choisir une position quelconque sur la sphère équatoriale (ascension droite α et déclinaison δ) et l'on peut faire évoluer la date et l'heure en temps universel (cela revient à faire tourner la Terre).
En bas de la simulation, on trouve les coordonnées calculées à partir des coordonnées équatoriales : angle horaire H, la hauteur h et l'azimut a.
Je vous propose de vérifier les points suivants :
- Placez-vous dans l'hémisphère nord en dehors de la bande intertropicale, à la longitude de Greenwich (L=0°,
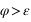 ) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h.
) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h. - Placez-vous dans l'hémisphère sud en dehors de la bande intertropicale, à la longitude de Greenwich (L=0°,
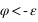 ), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h.
), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h. - Pour une latitude nord proche de Paris (φ=49°), vérifier que les étoiles dont la déclinaison est supérieure à 90°-φ= 41° ne se couche pas. Vérifier que les étoiles dont la déclinaison est supérieure à 49° présentent une plus grande digression est et ouest et qu'elles passent au méridien supérieur (H=0°) et au méridien inférieur (H=12h) au nord (a=180°).Vérifier que les étoiles qui ont une déclinaison égale à la latitude du lieu passe au zénith du lieu.
- Faire la même chose avec un lieu de l'hémisphère sud.
Les nouveaux repères
Auteur: Patrick Rocher
Les nouveaux systèmes de reférence
 introduction
introduction
Nous venons de voir que le repère terrestre et le repère céleste sont liés, car on détermine les latitudes et longitudes géographiques à l’aide de mesures astronomiques (hauteur des astres et passage au méridien). Les deux repères ne sont donc pas indépendants. De plus le repère céleste écliptique dépend de la théorie du barycentre Terre-Lune et le repère équatorial dépend des théories de la précession et de la nutation.
D’où l’idée de construire de nouveaux repères indépendants. Dans la construction de ces repères on distingue le concept et sa réalisation.
 Le système de référence céleste international (ITCS) et sa réalisation (ICRF)
Le système de référence céleste international (ITCS) et sa réalisation (ICRF)
L’International Celestial Reference System (ICRS) est le concept du système de référence céleste. Ce système contient l'ensemble des prescriptions et des conventions avec les modélisations nécessaires pour définir à tout moment un repère triaxial. L’International Celestial Reference Frame (ICRF) est une réalisation de ce concept basée sur l’orientation depuis le barycentre du système solaire d’un grand nombre de radios sources extragalactiques.
 Le système de référence terrestre international (ITRS) et sa réalisation (ITRF)
Le système de référence terrestre international (ITRS) et sa réalisation (ITRF)
L’International Terrestrial Reference System (ITRS) constitue un ensemble de prescriptions et de conventions avec les modélisations nécessaires pour définir l'origine, échelle, l'orientation et l'évolution dans le temps d’un système de référence terrestre conventionnel (CTRS). L'ITRS est un système de référence idéal, défini par la résolution n°2 UGCI (adoptée à Vienne en 1991).
L’ITRF (repère terrestre international) est une réalisation du système de référence terrestre international (ITRF), obtenu à l’aide des estimations des coordonnées et des vitesses d'un ensemble de stations terrestres observées par radio interférométrie à longue base (VLBI), télémétrie laser sur la Lune (LLR), mesure GPS, télémétrie laser sur satellites (SLR) et mesures Doppler de positionnement satellitaire (DORIS).
Nouvelles méthodes de calcul
Pour l’élaboration des éphémérides terrestres des astres, on est contraint de passer des coordonnées du repère céleste (ICRF) dans des coordonnées liées à la Terre (ITRF). Ce passage se fait en deux étapes :
On passe, à l’aide de transformations relativistes strictes, dans un système céleste géocentrique sans rotation (GCRS). Puis on passe du système céleste géocentrique au système terrestre (ITRS).
Réponses aux QCM
pages_repere-locaux/utilisation-simulations.html
QCM
'Systèmes de coordonnées'
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 1)
- Question 3
Solution : réponse 2)
- Question 4
Solution : réponse 2)
- Question 5
Aide :
Commencer par chercher la valeur de la déclinaison pour laquelle la hauteur est maximum à l'aide de la première simulation, en prenant en compte la réponse à la question précédente. Vérifier qu'un changement d'ascension droite ne modifie pas le résultat.
Aide :
A partir de la déclinaison, on peut obtenir l'ascension droite correspondante à l'aide de la deuxième simulation.
Solution : réponse 1)
- Question 6
Solution : réponse 2)
- Question 7
Solution : réponse 3)
- Question 8
Solution : réponse 3)
pages_applications/mctc-qcm-reperage.html
QCM
'QCM sur le repérage d'un astre'
- Question 1
Solution : réponse 2)
(
Les deux dernières réponses sont bonnes
)
Solution : réponse 3)
(
Les deux dernières réponses sont bonnes
)
- Question 2
Solution : réponse 1)
(
oui, l'angle horaire se compte à partir de la direction du Sud dans le repère équatorial local
)
- Question 3
Solution : réponse 3)
(
oui, c'est le moyen de trouver l'origine des ascensions droites dans le ciel : le temps sidéral n'est pas un temps mais un angle.
)
- Question 4
Solution : réponse 2)
- Question 5
Solution : réponse 2)
(
oui pour les astronomes (mais les géomètres mesurent les azimuts à partir du Nord)
)
- Question 6
Solution : réponse 1)
(
Avec un instrument méridien, l'angle horaire est nul: Le temps sidéral local est égal à l'ascension droite au moment du passage au méridien.
)
Solution : réponse 2)
(
Avec un instrument méridien, l'angle horaire est nul. L'instrument méridien observe exclusivement vers le Sud
)
Réponses aux exercices
pages_defrepere/mctc-application-sphere.html
Exercice
'La sphère céleste'
pages_defrepere/calculcoordpolaire.html
Exercice
'Calcul de coordonnées polaires'
pages_defrepere/calculpolaire3d.html
Exercice
'Calcul de coordonnées polaires'
pages_defrepere/conversion.html
Exercice
'Conversion des unités'
pages_defrepere/mctc-exo-repere-equatorial.html
Exercice
'Le repère écliptique'
- Question 1
Aide :
Dans l'hémisphère nord le Soleil culmine dans le ciel le jour du solstice d'été et il est au plus bas le jour du solstice d'hiver.
Ne pas oublier que le Soleil est toujours dans l'écliptique été comme hiver et que l'écliptique est toujours visible dans le ciel jour et nuit.
pages_defrepere/relation-ecliptique-equatoriale.html
Exercice
'Calcul des coordonnées équatoriales du Soleil'
pages_defrepere/calcul-latitude-geocentrique.html
Exercice
'Calcul de la latitude géocentrique de Paris'
pages_defrepere/mctc-exo-temps-sideral.html
Exercice
'Le temps sidéral'
pages_defrepere/variation-temps-sideral.html
Exercice
'Calcul du temps sidéral local en un lieu donné'
pages_defrepere/utilisation-simulations.html
Exercice
'Visibilité des étoiles'
- Question 1
Aide :
Attention au décalage horaire !
Pour simplifier, on pourra prendre minuit heure locale sans tenir compte des différences heures d'été / heures d'hiver.
Aide :
Par convention, la longitude est positive vers l'Est. Donc 140° E = +140°.
- Question 2
- Question 3
pages_defrepere/exercice-meridien.html
Exercice
'Passage du Soleil au méridien'
pages_defrepere/mctc-exo-declinaison.html
Exercice
'La déclinaison d'une étoile au zénith'
 Introduction
Introduction


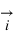 , ce vecteur porte donc le nom de vecteur unitaire.
, ce vecteur porte donc le nom de vecteur unitaire.
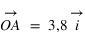 et que
et que 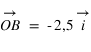 .
.
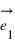 et
et 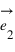 ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
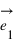 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 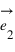 ; et sur l'axe portant le vecteur
; et sur l'axe portant le vecteur 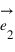 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 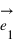 . Les coordonnées
. Les coordonnées 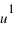 et
et 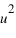 du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire : 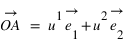 , les coordonnées
, les coordonnées 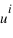 sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).
sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).





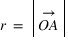 du point A au centre O du repère et l’angle entre la direction OA et l’un des axes. L'angle est compté positivement dans le sens direct (sens inverse des aiguilles d'une montre), souvent à partir de l'axe Ox
du point A au centre O du repère et l’angle entre la direction OA et l’un des axes. L'angle est compté positivement dans le sens direct (sens inverse des aiguilles d'une montre), souvent à partir de l'axe Ox
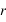 ,
,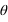 ) par les relations mathématiques suivantes :
) par les relations mathématiques suivantes :
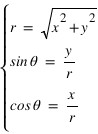 Les deux dernières relations peuvent être remplacées par
Les deux dernières relations peuvent être remplacées par 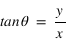 , mais l'on doit alors choisir le bon angle
, mais l'on doit alors choisir le bon angle 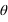 et fonction des signes de
et fonction des signes de 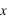 et de
et de 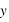
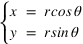
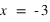 et
et 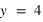 .
.

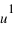 ,
,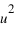 et
et 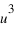 du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire : 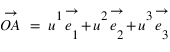 , les coordonnées
, les coordonnées 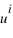 sont appelées coordonnées contravariantes du vecteur
sont appelées coordonnées contravariantes du vecteur 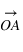 (ou projections parallèles). Elles sont souvent notées (x,y,z).
(ou projections parallèles). Elles sont souvent notées (x,y,z).
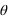 ,
,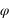 ) et une distance
) et une distance 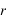 . L’angle
. L’angle 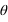 est l’angle entre la projection OA’ de OA dans le plan (Oxy) et l’axe Ox. L’angle
est l’angle entre la projection OA’ de OA dans le plan (Oxy) et l’axe Ox. L’angle 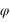 est l’angle entre OA et sa projection OA’. r est la distance entre l’origine O est le point A.
est l’angle entre OA et sa projection OA’. r est la distance entre l’origine O est le point A.
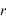 ,
,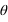 ,
,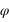 ) aux coordonnées cartésiennes (x,y,z) grâce aux relations suivantes :
) aux coordonnées cartésiennes (x,y,z) grâce aux relations suivantes :
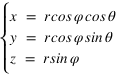
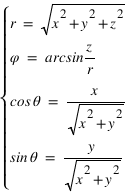
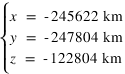 Calculer les coordonnées polaires (
Calculer les coordonnées polaires (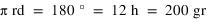
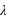 ) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée
) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée 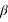 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.

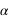 ) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée
) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée 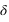 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée 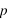 ).
).



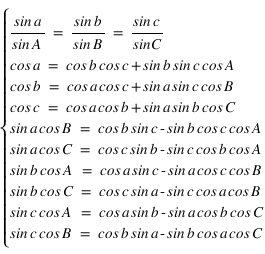

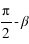 ,
,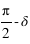 ,
,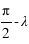 ,
,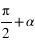 .
.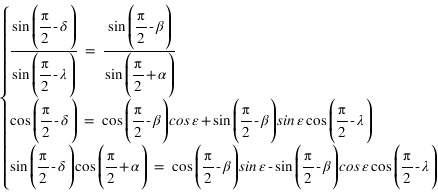
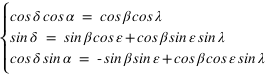
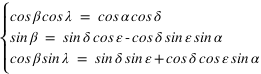
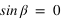 et que
et que 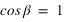 . Le système (1) est donc simplifié.
. Le système (1) est donc simplifié.
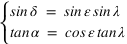 .
Faites attention aux unités, la calculatrice en ligne utilise des radians !
.
Faites attention aux unités, la calculatrice en ligne utilise des radians !


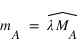 , sa longitude écliptique étant
, sa longitude écliptique étant 


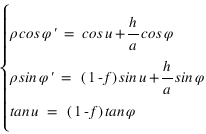
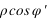 et
et 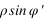 est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
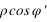 et
et 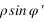 .
.


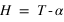
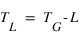
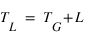
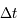 et la variation
et la variation 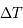 du temps sidéral :
du temps sidéral :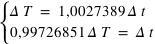


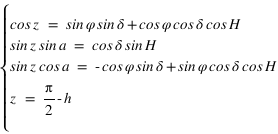
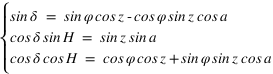




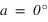 et
et 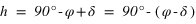 équation (1)
équation (1)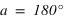 et
et 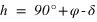 équation (2)
équation (2)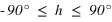 .
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si
.
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si 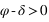 donc si
donc si 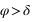 . Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si
. Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si 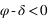 donc si
donc si 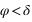 . Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors
. Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors 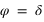 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.

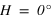 ) les équations de transformations de coordonnées donnent :
) les équations de transformations de coordonnées donnent :
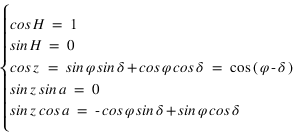
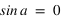 alors
alors 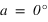 ou
ou 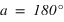 , si
, si 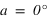 alors
alors 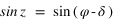 et si
et si 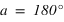 alors
alors 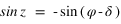 .
.
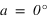 et
et 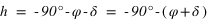 équation (3)
équation (3)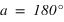 et
et 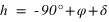 équation (4)
équation (4)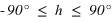 . On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si
. On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si 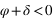 donc si
donc si 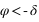 . Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si
. Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si 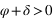 donc si
donc si 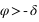 . Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors
. Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors 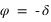 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.

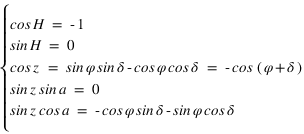
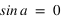 alors
alors 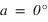 ou
ou 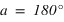 . Si
. Si 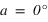 alors
alors 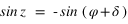 et si
et si 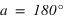 alors
alors 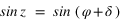 .
.
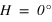
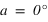
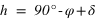
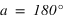
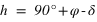
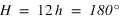
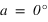
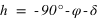
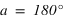
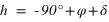
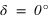 ) et le méridien supérieur => équation (1) ou (2) avec h positif.
) et le méridien supérieur => équation (1) ou (2) avec h positif.
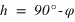 (colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
(colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
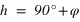 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
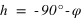 et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
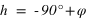 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
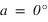 et
et 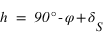 équation (1)
équation (1)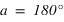 et
et 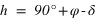 équation (2)
équation (2)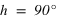 , alors a n’est plus défini, et :
, alors a n’est plus défini, et : 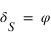
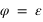 la solution est
la solution est 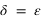 , donc le Soleil passe au zénith le jour du solstice d’été de juin. Un raisonnement identique pour le tropique du Capricorne montre que le Soleil passe au zénith uniquement le jour du solstice d’été de l’hémisphère sud. Sur l’équateur
, donc le Soleil passe au zénith le jour du solstice d’été de juin. Un raisonnement identique pour le tropique du Capricorne montre que le Soleil passe au zénith uniquement le jour du solstice d’été de l’hémisphère sud. Sur l’équateur 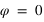 le Soleil passe au zénith deux fois par an lorsque sa déclinaison est nulle, c’est-à-dire aux équinoxes.
le Soleil passe au zénith deux fois par an lorsque sa déclinaison est nulle, c’est-à-dire aux équinoxes.
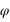 , quelle sera la déclinaison de cette étoile ?
, quelle sera la déclinaison de cette étoile ?

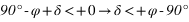
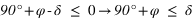
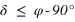 . De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant
. De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant 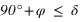 . Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
. Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
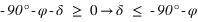
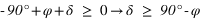
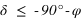 .
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant
.
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant 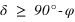 .
.
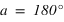 ) donc
) donc 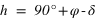 doit être inférieur à 90° donc
doit être inférieur à 90° donc 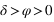 .
.
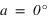 ) donc
) donc 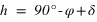 doit être inférieur à 90° donc
doit être inférieur à 90° donc 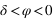 .
.
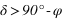 équation (1)
équation (1)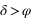 équation (2)
équation (2)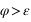 ) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h.
) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h.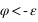 ), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h.
), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h.