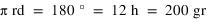Nous vivons et nous observons dans un espace à trois dimensions. Toute étude de mouvement dans notre environnement demande de positionner les corps par rapport à un repère de dimension trois. Le but du présent chapitre est de rappeler les notions de repère dans l'espace et les méthodes mathématiques qui permettent de changer de type de repère. On n'abordera pas dans ce chapitre la notion d'espace relativiste qui introduit le temps local comme quatrième dimension.
Vecteur unitaire sur un axe
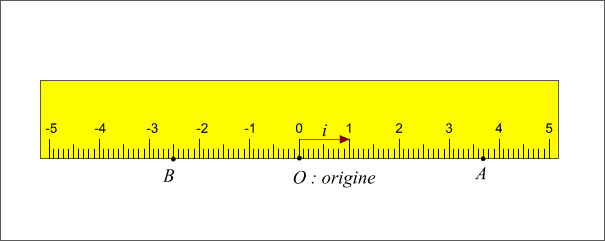
Figure 1: Vecteur unitaire sur un axe.
Crédit :
ASM/Patrick Rocher
On remarquera que nous n'avons pas indiqué d'unité de mesure sur le dessin, l'unité de mesure est la longueur du vecteur 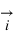 , ce vecteur porte donc le nom de vecteur unitaire.
, ce vecteur porte donc le nom de vecteur unitaire.
On peut également écrire que 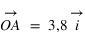 et que
et que 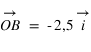 .
.
On remarquera également que chaque point de l'axe a une coordonnée et qu'inversement à chaque coordonnée correspond un point de l'axe. Cette propriété mathématique, appelée bijection entre le droite et l’ensemble des nombres réels, est fondamentale, car c’est elle qui permet de faire de la géométrie analytique.
Nota Bene : En mathématiques, le mot espace n'a pas le sens courant. Le 'plan' courant est un espace à 2 dimensions en mathématique et l''espace' courant est un espace à 3 dimensions en mathématiques. Il n'y a pas de mot courant pour les espaces à 4 (et plus) dimensions.
Pour pouvoir se positionner dans le plan, on doit définir un repère ayant la même dimension que le plan : la dimension deux. Pour cela on utilise deux vecteurs unitaires notés 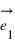 et
et 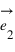 ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
Pour connaître la position d'un point A dans le plan par rapport au repère défini par les deux vecteurs, on va projeter le point A sur l'axe portant le vecteur 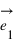 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 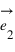 ; et sur l'axe portant le vecteur
; et sur l'axe portant le vecteur 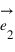 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 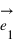 . Les coordonnées
. Les coordonnées 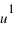 et
et 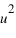 du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire : 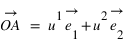 , les coordonnées
, les coordonnées 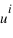 sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).
sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).
Repère quelconque
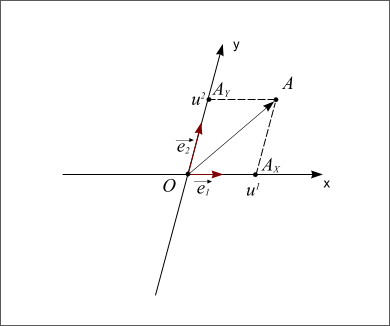
Figure 2: Repère direct quelconque
Crédit :
ASM/Patrick Rocher
Si les deux vecteurs sont perpendiculaires, le repère est dit orthogonal. Si les deux vecteurs ont la même longueur, on dit que le repère est normé. Et si les deux vecteurs sont perpendiculaires et s'ils ont la même longueur alors le repère est dit orthonormé. L'axe Ox porte le nom d'axe des abscisses et l'axe Oy porte le nom d'axe des ordonnées. Enfin si l'on passe de l'axe Ox à l'axe Oy par une rotation dans le sens inverse des aiguilles d'une montre (sens trigonométrique ou sens direct) on dit que le repère est direct. Dans le cas inverse, le repère est dit indirect.
Repère normé
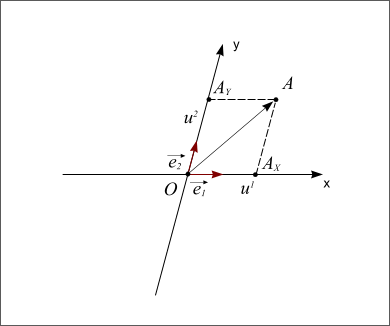
Figure 3 : Repère normé
Crédit :
ASM/Patrick Rocher
Repère orthonormé
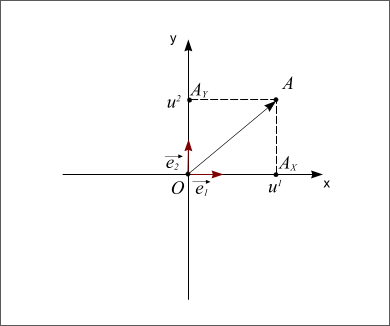
Figure 4 : Repère orthonormé
Crédit :
ASM/Patrick Rocher
Changement d’origine d’un repère
L'usage de repère cartésien est très répandu, on l'utilise systématiquement lorsque l'on trace un graphique. Il est souvent intéressant de pouvoir déplacer le repère sans pour autant changer l'orientation de ses deux axes. On dit alors que le repère est en translation. Pour un point quelconque du plan, on distingue deux possibilités :
- Le point A est lié au repère, dans ce cas la position du point A dans le repère translaté est la même.
- Le point A n'est pas lié au repère, dans ce cas le point A ne se déplace pas avec le repère et ses coordonnées dans le repère translaté ne sont plus les mêmes.
Figure 5 : Point A lié au repère translaté
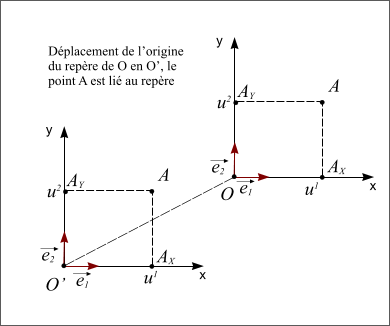
Figure 5 : Point A lié au repère translaté.
Crédit :
ASM/Patrick Rocher
Figure 6 : Point A non lié au repère tranlaté.
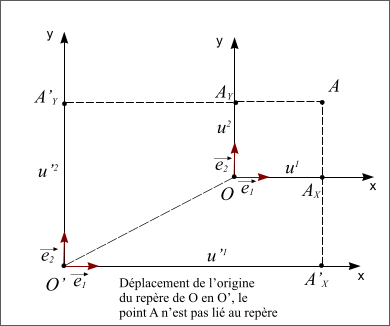
Figure 6 : Point A non lié au repère translaté.
Crédit :
ASM/Patrick Rocher
Rotation de repère
On peut également faire tourner le repère autour de son origine O, dans ce cas on peut également distinguer les points liés au repère qui vont tourner avec lui (dans ce cas leurs coordonnées ne changeront pas) et les points non liés au repère qui ne tourneront pas avec lui (dans ce cas leurs coordonnées vont changer).
Auteur: P. Rocher
 Calcul de coordonnées polaires
Calcul de coordonnées polaires
Soit un point A dans un repère orthonormé dont les coordonnées cartésiennes sont 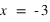 et
et 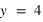 .
.
Question 1)
Calculer les coordonnées polaires de ce point , l'angle sera donné en degrés ?
Utiliser les formules du cours, attention aux unités pour l'angle si vous utilisez votre calculette.
Coordonnées cartésiennes
Pour se positionner dans l’espace, il convient d’ajouter une troisième dimension. Tout ce que nous avons dit pour les repères à deux dimensions se transpose pour les repères à trois dimensions.
La figure suivante représente un repère orthonormé direct, le troisième axe est l’axe Oz.
Repère orthonormé direct
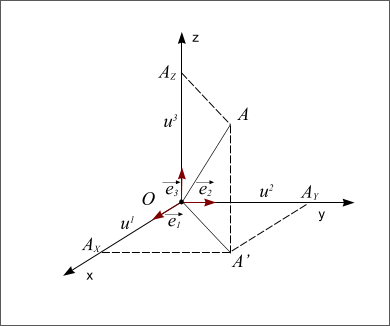
Figure 7 : Repère orthonormé direct.
Crédit :
ASM/Patrick Rocherr
Le point A est projeté orthogonalement en A’ sur le plan Oxy, puis A’ est projeté en AX sur l’axe Ox et en AY sur l’axe Oy. Le point A est également projeté orthogonalement en AZ sur l’axe Oz. Les coordonnées 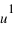 ,
,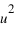 et
et 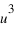 du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire : 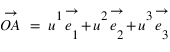 , les coordonnées
, les coordonnées 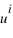 sont appelées coordonnées contravariantes du vecteur
sont appelées coordonnées contravariantes du vecteur 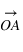 (ou projections parallèles). Elles sont souvent notées (x,y,z).
(ou projections parallèles). Elles sont souvent notées (x,y,z).
Le poids des traditions est très fort dans nos cultures, la standardisation des unités de mesure n’est pas toujours suivie d’effet et l’on trouve encore en fonction des pays et des publications des usages non standards. Ainsi les Anglo-saxons utilisent le mille terrestre international plus souvent que le mètre et les cartographes français utilisent encore le grade pour mesure les longitudes et les latitudes terrestres !
Les angles plans sont mesurés avec quatre systèmes d’unités :
Le radian
Le radian. La mesure d’un angle en utilisant cette unité se fait en radian et en fraction décimale de radian. C’est l’unité que l’on doit utiliser dans les calculs, en effet lorsque l'on dérive ou intègre une fonction trigonométrique l’angle doit être exprimé en radian.
Le degré sexagésimal
Le degré sexagésimal Cette unité est très ancienne, elle est basée sur le système sexagésimal qui permettait de faire des divisions facilement à l’époque où l’on connaissait mal les fractions. Le degré se divise en 60 minutes (symbole : ′), la minute se divise en 60 secondes (symbole : ″) etc. Dans le passé on divisait la seconde en 60 tierces (symbole : ′″) qui était elle-même divisée en 60 quatrièmes (symbole : IV). De nos jours on utilise plus les divisions inférieures à la seconde (on utilise les fractions décimales de la seconde), mais vous trouverez les anciennes notations dans les livres anciens. On remarquera que les symboles (′ - ″ - ′″ - IV ) correspondent à la numérotation romaine (I, II, III, IV) mise en exposant.
L'heure sexagésimale
L’heure sexagésimale L’heure se divise en 60 minutes (symbole : min), la minute se divise en 60 secondes (symbole : s). Il n’y a pas de divisions inférieures à la seconde (on utilise les fractions décimales de la seconde). Cette unité est encore largement utilisée en astronomie. Attention c’est une unité angulaire et non une unité de temps. L’unité de temps est définie à partir de la définition de la seconde de temps.
Le grade centésimal
Le grade centésimal Ce système est centésimal, ainsi le grade se divise en 100 minutes (symbole : ′) centésimales, la minute centésimale se divise en 100 secondes centésimales (symbole : ″) etc. On retrouve ici l’avantage du système centésimal, 23gr 35′ 25″ est égale à 23,3525 gr et si l’on prend le quadrant (angle droit) comme unité 0,233525 est directement le rapport de l’angle à l’angle droit.
On a les relations suivantes entre les différentes unités : 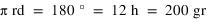

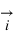 , ce vecteur porte donc le nom de vecteur unitaire.
, ce vecteur porte donc le nom de vecteur unitaire.
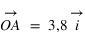 et que
et que 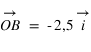 .
.
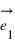 et
et 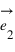 ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
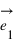 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 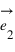 ; et sur l'axe portant le vecteur
; et sur l'axe portant le vecteur 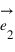 parallèlement à la droite portant le vecteur
parallèlement à la droite portant le vecteur 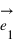 . Les coordonnées
. Les coordonnées 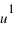 et
et 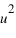 du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire : 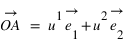 , les coordonnées
, les coordonnées 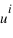 sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).
sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).





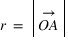 du point A au centre O du repère et l’angle entre la direction OA et l’un des axes. L'angle est compté positivement dans le sens direct (sens inverse des aiguilles d'une montre), souvent à partir de l'axe Ox
du point A au centre O du repère et l’angle entre la direction OA et l’un des axes. L'angle est compté positivement dans le sens direct (sens inverse des aiguilles d'une montre), souvent à partir de l'axe Ox
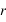 ,
,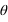 ) par les relations mathématiques suivantes :
) par les relations mathématiques suivantes :
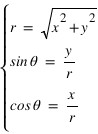 Les deux dernières relations peuvent être remplacées par
Les deux dernières relations peuvent être remplacées par 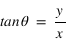 , mais l'on doit alors choisir le bon angle
, mais l'on doit alors choisir le bon angle 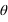 et fonction des signes de
et fonction des signes de 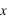 et de
et de 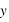
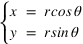
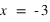 et
et 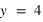 .
.

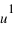 ,
,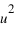 et
et 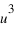 du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire : 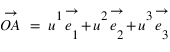 , les coordonnées
, les coordonnées 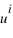 sont appelées coordonnées contravariantes du vecteur
sont appelées coordonnées contravariantes du vecteur 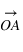 (ou projections parallèles). Elles sont souvent notées (x,y,z).
(ou projections parallèles). Elles sont souvent notées (x,y,z).
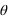 ,
,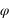 ) et une distance
) et une distance 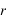 . L’angle
. L’angle 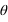 est l’angle entre la projection OA’ de OA dans le plan (Oxy) et l’axe Ox. L’angle
est l’angle entre la projection OA’ de OA dans le plan (Oxy) et l’axe Ox. L’angle 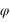 est l’angle entre OA et sa projection OA’. r est la distance entre l’origine O est le point A.
est l’angle entre OA et sa projection OA’. r est la distance entre l’origine O est le point A.
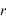 ,
,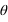 ,
,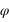 ) aux coordonnées cartésiennes (x,y,z) grâce aux relations suivantes :
) aux coordonnées cartésiennes (x,y,z) grâce aux relations suivantes :
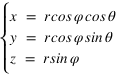
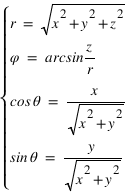
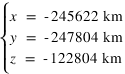 Calculer les coordonnées polaires (
Calculer les coordonnées polaires (