Les repères de l'astronomie "fixes"
- Introduction
- Les repères quasi fixes
- Le repère céleste écliptique
- Exercice
- Le repère céleste équatorial
- Changement de repère
- Formulaire de trigonométrie sphérique
- Relations entre les coordonnées polaires écliptiques et équatoriales
- Position du Soleil sur l'écliptique
- Les mouvements du repère équatorial
- La médiation
- Le repère galactique J2000
- Les coordonnées terrestres
- Calcul des coordonnées géocentriques
Introduction
Nous allons décrire les repères astronomiques classiques. Ces dernières années, l’amélioration croissante de la précision des observations a nécessité des réformes importantes et la création de nouveaux repères célestes et terrestres que nous aborderons que très succinctement dans les pages « pour en savoir plus ».
Les repères quasi fixes
Historiquement, deux plans fondamentaux se sont imposés. Le premier est le plan de l’orbite apparente du Soleil vue depuis la Terre. Plus rigoureusement, il s'agit du plan de l'orbite du barycentre Terre-Lune. Ce plan est appelé écliptique, car c’est lorsque la Lune est proche de ce plan qu’il y a possibilité d’éclipse. Le Soleil, la Lune et les planètes sont toujours très proches de ce plan. Ce repère écliptique est utilisé pour étudier les mouvements des objets du système solaire.'
L’autre plan est le plan de l’équateur terrestre. Ce repère, le repère céleste équatorial est le repère principal pour les astrophysiciens (terriens!). Dans ce repère, les étoiles ont des coordonnées fixes.
Les astronomes ont construit un repère fondamental avec chacun de ces plans. Comme ces plans ne sont pas totalement fixes, ces repères sont définis pour un instant donné, par exemple pour l’instant correspondant au 1er janvier 2000 à 12h que l’on nomme époque J2000. De plus comme l’astronome observe et mesure uniquement des angles, on se limite souvent à des coordonnées polaires sur une sphère de rayon unité appelée sphère céleste.
Le repère céleste écliptique
Le repère écliptique J2000 est défini par le plan de base (Oxy) correspondant à l’orbite osculatricedu barycentre Terre-Lune autour du Soleil, la direction de l’axe Oz normale à ce plan (appelée pôle de l’écliptique) est choisie de sorte que le mouvement du barycentre Terre-Lune se fasse dans le sens direct (sens inverse des aiguilles d’une montre). Dans ce repère les coordonnées portent le nom de coordonnées écliptiques J2000. Les deux coordonnées polaires sont respectivement la longitude écliptique et la latitude écliptique. La longitude (notée 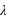 ) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée
) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée 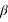 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.
Repère écliptique
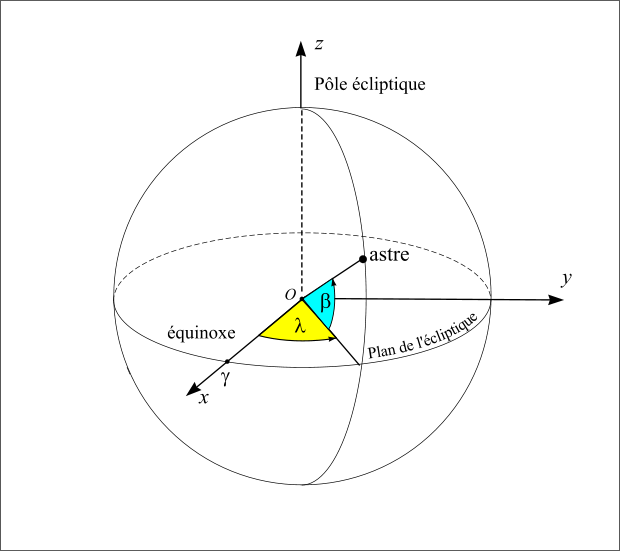
Figure 8 : Repère écliptique.
Crédit :
ASM/Patrick Rocher
Exercice
 Le repère écliptique
Le repère écliptique
Question 1)
Sachant que toutes les planètes se trouvent, comme le Soleil, dans l'écliptique ou très proches de l'écliptique, quelles sont, dans l’hémisphère nord, les meilleures conditions pour observer les planètes extérieures (Mars, Jupiter, Saturne, Uranus et Neptune) au plus haut dans le ciel nocturne ?
Dans l'hémisphère nord le Soleil culmine dans le ciel le jour du solstice d'été et il est au plus bas le jour du solstice d'hiver.
Ne pas oublier que le Soleil est toujours dans l'écliptique été comme hiver et que l'écliptique est toujours visible dans le ciel jour et nuit.
Le repère céleste équatorial
Le repère céleste équatorial
Le repère équatorial J2000 est défini par le plan de base (Oxy) correspondant au plan de l’équateur céleste (plan parallèle à l’équateur terrestre passant par le centre du repère) à l’instant considéré, la direction de l’axe Oz normale à ce plan (appelée pôle céleste nord) est choisie de sorte que le mouvement de la Terre autour de cet axe se fasse dans le sens direct (sens inverse des aiguilles d’une montre – donc d’ouest en est). Dans ce repère les coordonnées portent le nom de coordonnées équatoriales J2000. Les deux coordonnées polaires sont respectivement l’ascension droite et la déclinaison. L’ascension droite (notée 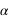 ) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée
) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée 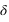 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée 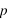 ).
).
Repère céleste équatorial
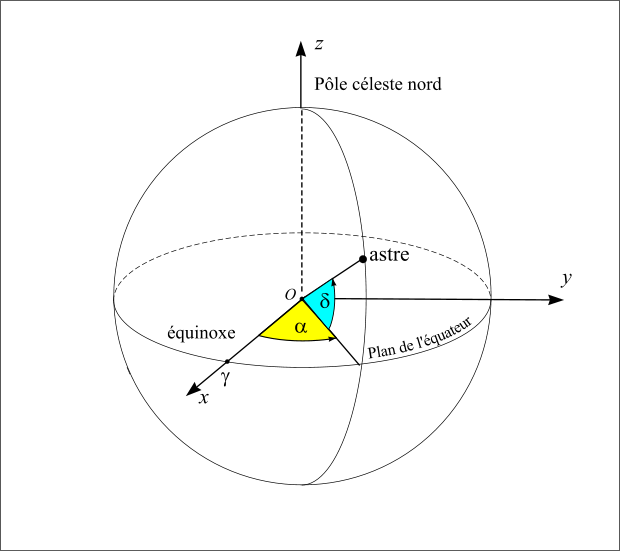
Figure 9 : Repère céleste équatorial.
Crédit :
ASM/Patrick Rocher
 Remarques
Remarques
On remarquera que nous n’avons pas encore précisé les directions origines Ox du repère écliptique et du repère équatorial. On pourrait définir des origines quelconques pour ces deux repères, mais comme l’axe de rotation de la Terre n’est pas perpendiculaire à son orbite, le plan de l’équateur n’est pas parallèle au plan de l’écliptique. L’intersection de ces deux plans est une droite que l’on nomme droite des équinoxes. Il était donc judicieux d’utiliser cette droite commune pour définir un axe Ox commun aux deux repères. Sur cette droite, on a le choix entre deux directions pour orienter l’axe Ox, on a choisi la direction de l’équinoxe correspondant au passage du Soleil des déclinaisons négatives aux déclinaisons positives dans son mouvement apparent annuel autour de la Terre. Cet équinoxe est appelé l’équinoxe de printemps ou point vernal. Il est noté pour la lettre gamma Υ, lettre grecque proche du symboledu signe du Bélier. La direction opposée est appelée direction de l’équinoxe d’automne, elle est notée par la lettre grecque oméga majuscule Ω proche du symbole du signe de la Balance.
Attention la direction de l’équinoxe de printemps est unique, elle ne change pas en fonction de l’hémisphère terrestre où l’on se trouve comme on le lit parfois. C’est le début de la saison astronomique qui change. Dans l’hémisphère nord le printemps commence lorsque le Soleil passe par l’équinoxe de printemps, cet instant correspond au début de l’automne dans l’hémisphère sud.
Changement de repère
Changement de repère
Les deux repères ayant le même axe Ox, on passe d’un repère à l’autre en faisant une rotation autour de cet axe Ox. Cet angle est l’angle que fait l’écliptique céleste avec l’équateur céleste. Il porte de nom d’obliquité de l’écliptique et est noté ε. Sa valeur à l’époque J2000 est proche de 23° 26' 21". Cet angle est également l’angle que fait l’axe de rotation de la Terre avec la normale à l’écliptique (pôle de l’écliptique).
Les deux repères (écliptique et équatorial).
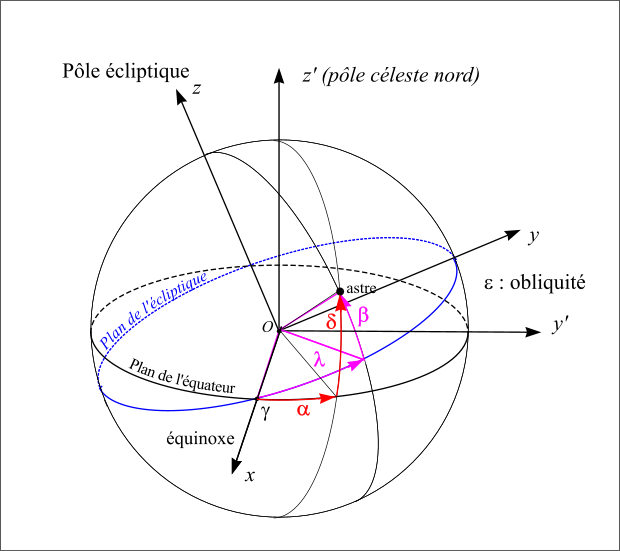
Figure 10 : Les deux repères (écliptique et équateur).
Crédit :
ASM/Patrick Rocher
Nouvelles définitions
Le grand cercle de la sphère céleste passant par les pôles célestes et les équinoxes porte le nom de colure des équinoxes. La droite perpendiculaire à la droite des équinoxes contenue dans le plan de l’écliptique porte le nom de droite des solstices. De même le grand cercle de la sphère céleste qui passe par les pôles célestes et les points solsticiaux porte le nom de colure des solstices. On remarquera que le colure des solstices passe également par les pôles de l’écliptique. Les colures des solstices et des équinoxes divisent l’équateur et l’écliptique en quatre secteurs égaux de 90°.
Selon l’origine des repères on parlera de :
- coordonnées barycentriques si l’origine est au barycentre du système solaire,
- coordonnées héliocentriques si l’origine est au centre de masse du Soleil,
- coordonnées géocentriques si l’origine est au centre de masse de la Terre,
- coordonnées topocentriques si l’origine est un lieu à la surface terrestre,
- coordonnées sélénocentriques si l’origine est au centre de masse de la Lune.
Formulaire de trigonométrie sphérique
Les formulaires de changement de repères en coordonnées polaires font appel à la trigonométrie sphérique.
Pour cela nous allons utiliser les formules de trigonométriques sphériques classiques.
Triangle sphérique
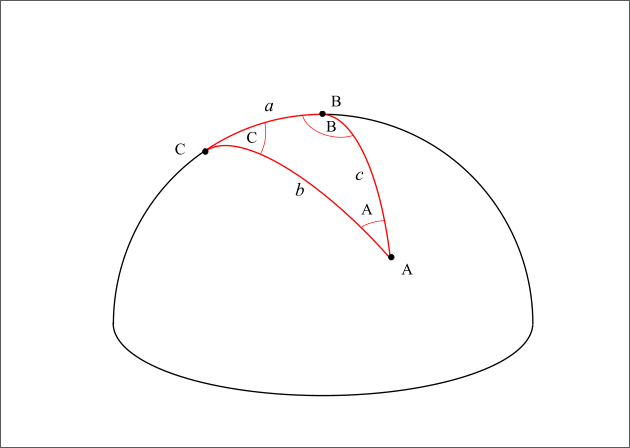
Figure 11 : Triangle sphérique.
Crédit :
ASM/Patrick Rocher
Considérons un triangle sphérique ABC formé par des arcs de grands cercles de la sphère, ce triangle possède trois angles aux sommets A, B et C et trois angles « côtés » a, b, c. A, B et C sont les angles entre les arcs de grands cercles et a, b et c sont les longueurs angulaires des arcs de grands cercles. Entre ces six angles, on a les relations trigonométriques suivantes :
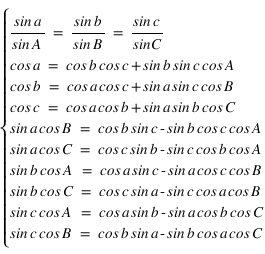
Il est inutile de connaître ces formules par cœur, il suffit de savoir qu’elles existent et de s’y rapporter lorsque l’on a un calcul à faire.
Relations entre les coordonnées polaires écliptiques et équatoriales
Si l’on trace les deux repères sur la sphère céleste et un astre quelconque en A, le pôle de l’écliptique PE, le pôle nord céleste P et la direction de l’astre A forme un triangle sphérique (PEPA).
Triangle sphérique, repères écliptique et équatorial.
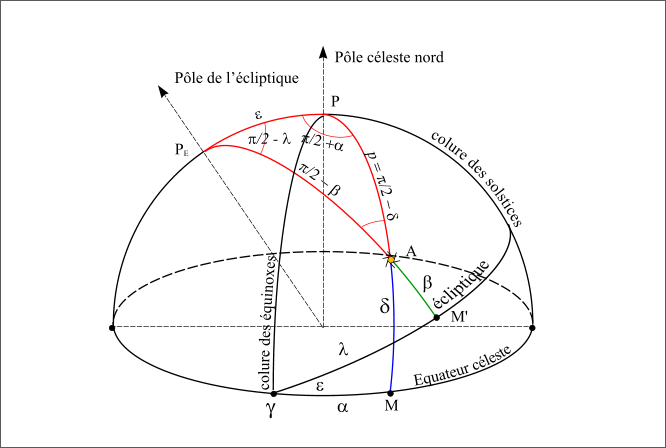
Figure 12 : Triangle sphérique, repères écliptique et équatorial.
Crédit :
ASM/Patrick Rocher
Dans ce triangle on connait cinq des six angles :
- L’arc PEP est l’obliquité ε,
- L’arc PEA est le complémentaire de la latitude écliptique :
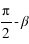 ,
, - L’arc PA est la distance polaire ou le complémentaire de la déclinaison :
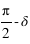 ,
, - L’angle entre l’arc PEP et l’arc PEA est le complémentaire de la longitude écliptique :
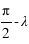 ,
, - L’angle entre PEP et PA est égal à 90° (π/2) l’angle entre les deux colures plus l’ascension droite de l’astre :
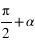 .
.
Pour avoir par exemple les coordonnées équatoriales en fonction des coordonnées écliptiques, il suffit d’écrire les relations suivantes :
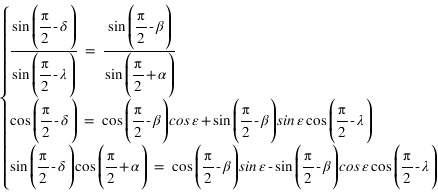
Ce qui donne après simplification :
Système (1) 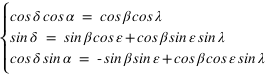
La déclinaison s’obtient à l’aide de la seconde relation en prenant l’arc sinus de sin δ (car δ est compris en –90° et +90°) l’ascension droite est obtenue grâce à la première et à la troisième relation. La connaissance du sinus et du cosinus de l’ascension droite permet de connaître l’ascension droite sur l’intervalle allant de 0° à 360°. On doit ensuite mettre ces deux variables dans le bon système d’unités (heures sexagésimales pour l’ascension droite et degrés sexagésimaux pour la déclinaison).
On a des relations identiques pour passer des coordonnées équatoriales aux coordonnées écliptiques.
Système (2) 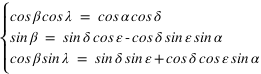
Auteur: ASM/Patrick Rocher
 Calcul des coordonnées équatoriales du Soleil
Calcul des coordonnées équatoriales du Soleil
Cet exercice a pour but de vous faire calculer les coordonnées équatoriales du Soleil à partir de ces coordonnées écliptiques.
Pour simplifier, le calcul on supposera que la latitude du Soleil β est nulle, ce qui implique que 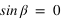 et que
et que 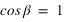 . Le système (1) est donc simplifié.
. Le système (1) est donc simplifié.
Question 1)
Le 1 janvier 2012 à 0h UTC, la longitude apparente λ du Soleil est de 279° 57' 30", calculer son ascension droite et sa déclinaison sachant que l'obliquité de l'écliptique ε à cet instant est de 23°26' 12,7". On exprimera l'ascension droite en heures, minutes et secondes d'angle et la déclinaison en dégres, minutes et secondes d'angle.
Le système (1) lorsque l'on prend une latitude nulle à la forme simplifier suivante : 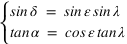 .
Faites attention aux unités, la calculatrice en ligne utilise des radians !
.
Faites attention aux unités, la calculatrice en ligne utilise des radians !
Position du Soleil sur l'écliptique
Position du Soleil sur l'écliptique 
Cette simulation a pour but de vous montrer le mouvement du Soleil apparent sur l'écliptique.
Elle montre l'inclinaison de l'écliptique sur l'équateur céleste (noté ε), la longitude écliptique du Soleil apparent et les coordonnées équatoriales (ascension droite α et déclinaison δ). P est le pôle Nord céleste et K est le pôle Nord de l'écliptique.
Dans cette simulation, la latitude du Soleil est supposée nulle, en réalité la latitude du Soleil est très faible et varie en fonction du temps. Cet écart provient du fait que l'écliptique est construit à partir du mouvement du barycentre Terre-Lune alors que les coordonnées du Soleil sont calculées depuis le centre de la Terre.
Remarques
Les coordonnées équatoriales du Soleil variant peu au court d'une journée, on peut utiliser cet applet pour calculer les coordonnées équatoriales du Soleil un jour donné.
On vérifiera deux choses importantes :
Auteur: P. Rocher
 Variation journalière de la longitude et de l'ascension droite du Soleil
Variation journalière de la longitude et de l'ascension droite du Soleil
Question 1)
Placez-vous le 5 janvier 2012, noter la longitude. Avancez d'un jour est refaite la même mesure. En déduire la variation journalière en longitude. Refaites la même mesure pour le 5 et le 6 juillet 2012. Que peut-on en déduire?
Question 2)
Le jour de l'équinoxe de printemps est le jour où la longitude du Soleil passe par 0°, celui de l'équinoxe d'automne est celui où la longitude du Soleil est égale à 180°. Les jours des solstices d'été et d'hiver correspondent respectivement au jour où la longitude du Soleil passe par 90° et 270°. Calculez les dates des saisons pour une année donnée.
Les mouvements du repère équatorial
En fait la direction de l’axe instantané de rotation de la Terre n’est pas constante. Historiquement le mouvement de cet axe a été décomposé en deux parties : une composante circulaire appelée précession et une composante formée de multiples variations périodiques appelée nutation. La composante circulaire fait parcourir à l’axe de rotation de la Terre un cône dans le sens rétrograde à la vitesse d’environ 50″ par an (un tour en environ 26000 ans). Cette précession se traduit par un mouvement de l’axe des équinoxes à la même vitesse également dans le sens rétrograde (appeler précession des équinoxes). On peut donc définir des repères écliptiques et équatoriaux dans lesquels on corrige de la précession, pour une date donnée, la position de l’équinoxe. Dans ce cas les repères sont dits moyens de la date.
On peut aussi définir des repères écliptiques et équatoriaux dans lesquels on corrige, pour une date donnée, la position de l’équinoxe de la précession et de la nutation (qui agit également sur l’obliquité de l’écliptique). Dans ce cas les repères sont dits vrais de la date.
On voit l’importance de la connaissance du mouvement de l’axe de rotation de la Terre.
On voit également que le repère écliptique dépend de la théorie du barycentre Terre-Lune et que l’usage d’une origine tournante, la direction de l’équinoxe n’est forcément judicieuse, car elle varie en fonction de la théorie de la précession utilisée.
Précession des équinoxes
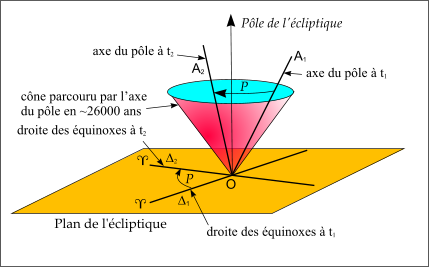
Figure 13 : Précession des équinoxes.
Crédit :
ASM/Patrick Rocher
La médiation
La médiation est une notation hybride basée sur les deux repères écliptique et équatorial. Considérons le cercle horaire portant l’astre A. Ce cercle horaire coupe l’équateur céleste en H et il coupe l’écliptique en MA que l’on nomme point de médiation de l’astre A. On appelle médiation de l’astre A l’arc 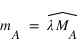 , sa longitude écliptique étant λ , M étant la projection de la direction de l’astre sur l’écliptique.
, sa longitude écliptique étant λ , M étant la projection de la direction de l’astre sur l’écliptique.
Parfois on donne le couple de coordonnées formé par la médiation et la déclinaison à la place des coordonnées équatoriales classiques (ascension droite et déclinaison). Ce couple de coordonnées n’est pas orthogonal, mais il est parfois utilisé notamment dans les instruments anciens (astrolabe).
La médiation d'un astre.
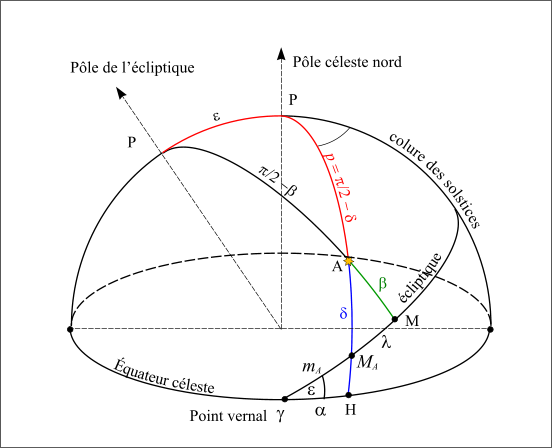
Figure 14 : La médiation d'un astre.
Crédit :
ASM/Patrick Rocher
Le repère galactique J2000
Les astronomes utilisent également un repère particulier pour positionner les étoiles par rapport au plan de notre galaxie : le repère galactique.
Le repère galactique
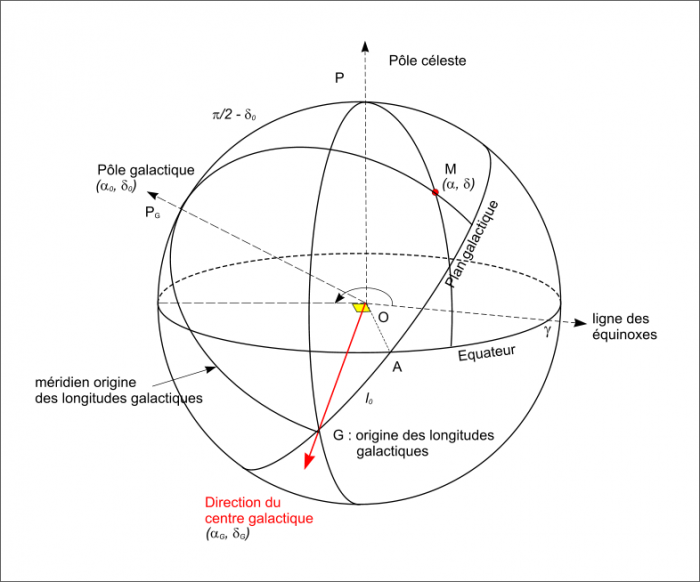
Figure 15 : Le repère galactique.
Crédit :
ASM/Patrick Rocher
Soit PG (α0, δ0) la direction du pôle galactique dans le repère équatorial J2000 et OG (αG, δG) la direction du centre galactique dans ce même repère. Les coordonnées géocentriques galactiques J2000, la longitude et latitude galactiques sont définies dans le repère direct construit à l’aide du plan galactique et le pôle galactique. Le méridien origine des longitudes étant défini par la direction du centre galactique. Nous noterons l0 l’angle AG (positif dans le sens rétrograde). L’ascension droite αA du point A est égale α0 + π/2 et l’inclinaison i du plan galactique sur l’équateur est égale à α0 – π/2. Le plan galactique ainsi défini est le plan passant par le centre de la Terre, normal à la direction du pôle galactique. Ce repère est un repère géocentrique J2000, car il est défini par rapport au repère fixe équatorial J2000.
Les coordonnées terrestres
Les coordonnées terrestres sont données par rapport au pôle terrestre et le plan de l’équateur terrestre. Ce système constitue un référentiel terrestre. Les coordonnées polaires terrestres portent les noms de latitude (notée φ) et longitude (notée L) terrestres. L’axe instantané de rotation de la Terre se déplace par rapport aux étoiles, mais il reste quasi fixe par rapport à la croûte terrestre.
Par contre la Terre n’étant pas parfaitement sphérique (elle est aplatie aux pôles), on doit distinguer deux types de coordonnées : des coordonnées géographiques (ou astronomiques) et des coordonnées géocentriques.
En première approximation la Terre est assimilée à un ellipsoïde de révolution.
Un méridien terrestre est un arc de longitude constante joignant les deux pôles terrestres.
Sur cet ellipsoïde on définit un méridien origine passant par les deux pôles géographiques. Ce méridien origine porte le nom de méridien international (méridien de Greenwich). Pour un lieu donné, on distingue une seule longitude et deux latitudes :
- la latitude géocentrique φ' qui est l’angle entre la direction allant du centre de la Terre au lieu considéré et le plan de l’équateur terrestre,
- la latitude géographique ou astronomique φ qui est l’angle entre la normale à l’ellipsoïde de référence et le plan de l’équateur terrestre.
coordonnées géographiques
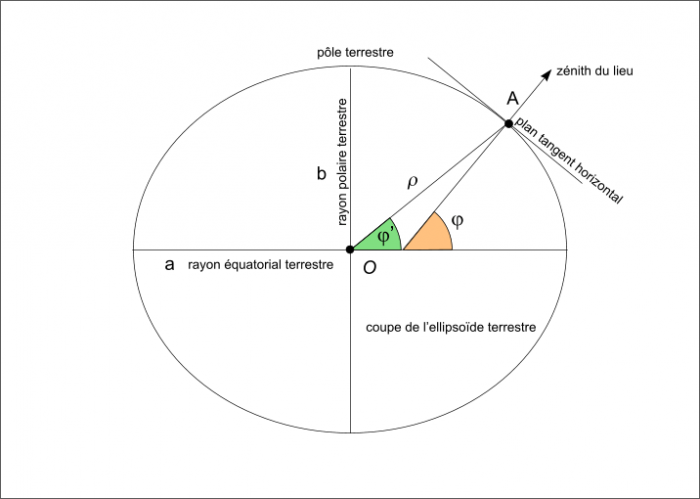
Figure 16 : Coordonnées géographiques.
Crédit :
ASM/Patrick Rocher
Historiquement les latitudes géographiques étaient obtenues à l’aide de mesures de hauteur d’astre aux dessus de l’horizon.
La longitude est comptée à partir du méridien international en heures ou en degrés sexagésimaux. Historiquement les longitudes géographiques étaient obtenues à l’aide de mesures astronomiques (point astronomique).
De nos jours les coordonnées géographiques sont obtenues à l’aide de systèmes satellitaires (GPS).
Sur une planète on parlera de coordonnées planétographiques et de coordonnées planétocentriques.
Calcul des coordonnées géocentriques
Soit φ la latitude géographique, φ' la latitude géocentrique et h l’altitude du lieu.
a est le rayon équatorial terrestre et f est l’aplatissement de l’ellipsoïde terrestre.
ρ est la distance entre le centre de la Terre et le lieu exprimé en rayon terrestre équatorial.
On a les relations suivantes :
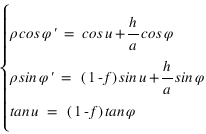
La connaissance des quantités 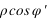 et
et 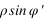 est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
Quelques ellipsoïdes de références
| Système géodésique | Ellipsoïde associé | aen mètres | b en mètres | f |
|---|
| NTF | Clarke 1880 IGN | 6378249,2 | 6356515,0 | 1/293,466021 |
| ED50 | ED50 Hayford 1909 | 6378388,0 | 6356911,9461 | 1/297,000000 |
| WGS84 et RGF 83 | IAG GRS 1980 | 6378137,0 | 6356752,314 | 1/298,257222 |
Auteur: P. Rocher
 Calcul de la latitude géocentrique de Paris
Calcul de la latitude géocentrique de Paris
Les coordonnées géographiques de l'Observatoire de Paris sont les suivantes :Latitude géographique : 48° 50' 11,2" N, longitude géographique : 2° 20' 13,8" E, altitude : 67m.
Question 1)
Calculer les coordonnées géocentriques de l’Observatoire de Paris en utilisant le système géodésique WGS84.
On calculera d'abord la valeur de u, puis les valeurs de 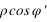 et
et 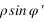 .
.
Réponses aux exercices
pages_defrepere/mctc-exo-repere-equatorial.html
Exercice
'Le repère écliptique'
- Question 1
Aide :
Dans l'hémisphère nord le Soleil culmine dans le ciel le jour du solstice d'été et il est au plus bas le jour du solstice d'hiver.
Ne pas oublier que le Soleil est toujours dans l'écliptique été comme hiver et que l'écliptique est toujours visible dans le ciel jour et nuit.
pages_defrepere/relation-ecliptique-equatoriale.html
Exercice
'Calcul des coordonnées équatoriales du Soleil'
pages_defrepere/calcul-latitude-geocentrique.html
Exercice
'Calcul de la latitude géocentrique de Paris'
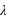 ) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée
) est comptée en degrés sexagésimaux de 0° à 360° à partir de l’origine Ox du repère et la latitude (notée 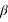 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’écliptique. Les grands cercles passant par les deux pôles de l’écliptique portent le nom de méridiens écliptiques, les petits cercles de la sphère céleste parallèles à l’écliptique portent le nom de parallèles écliptiques.

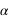 ) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée
) est comptée en heures sexagésimales de 0h à 24h à partir de l’origine Ox du repère et la déclinaison (notée 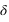 ) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée
) est comptée en degrés sexagésimaux de –90° à +90° à partir du plan de l’équateur céleste. On utilise parfois à la place de la déclinaison l’angle entre le pôle céleste et la direction de l’astre, cet angle est compté positivement de 0° à 180° à partir du pôle céleste nord et porte le nom de distance polaire (notée 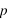 ).
).



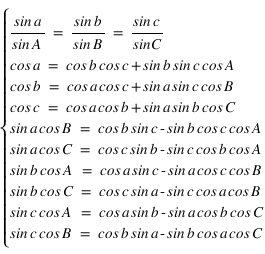

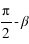 ,
,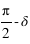 ,
,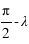 ,
,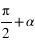 .
.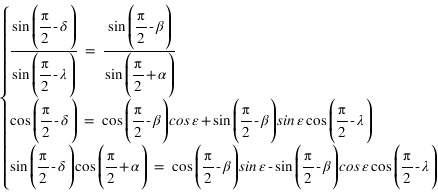
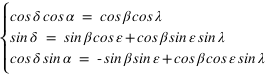
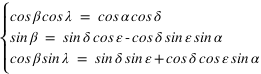
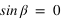 et que
et que 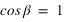 . Le système (1) est donc simplifié.
. Le système (1) est donc simplifié.
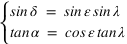 .
Faites attention aux unités, la calculatrice en ligne utilise des radians !
.
Faites attention aux unités, la calculatrice en ligne utilise des radians !


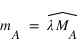 , sa longitude écliptique étant
, sa longitude écliptique étant 


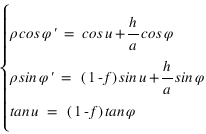
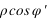 et
et 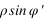 est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
est très importante, car elles servent à calculer le vecteur centre de la Terre – observateur, vecteur qui permet de passer des coordonnées géocentriques aux coordonnées topocentriques. Il existe de nombreux ellipsoïdes de références, voici ceux utilisés en France.
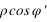 et
et 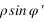 .
.