
 Temps de réponse
Temps de réponse
Difficulté : ☆
Temps : 10 min
Une observation astérosismique avec le spectromètre HARPS nécessite
la lecture d'une caméra de 2k×4k. Par ailleurs, l'échantillonnage du signal temporel nécessite l'acquisition d'une image par minute.
Question 1)
Déterminer le temps de pose en fonction de la magnitude, sachant que le détecteur sature à partir de 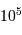 photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.
photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.
AideSolution
Rappel : magnitude et luminosité varient dans le rapport :
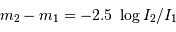
Par application de la définition de la magnitude, le flux d'une étoile de magnitude 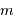 vaut
vaut 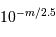 par rapport à celui d'une étoile de magnitude nulle.
par rapport à celui d'une étoile de magnitude nulle.
Le temps de pose étant limité par le flux optimal sur un pixel, une pose de durée 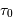 pour une magnitude nulle sera multipliée par
pour une magnitude nulle sera multipliée par 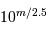 pour une magnitude
pour une magnitude 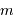 .
.
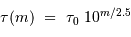
Soit 10 s pour une magnitude 2.5, 100 s pour une magnitude 5.
Question 2)
Le temps de lecture de la caméra est de 20 s. Pour quelle magnitude minimale l'observation reste-t-elle pertinente, avec au-moins la moitié du temps passée sur la source et non à lire la caméra ?
Solution
En application de ce qui précède, une pose de 20 s correspond à la magnitude 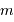 vérifiant
vérifiant
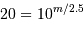 , càd
, càd 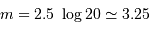 .
.
Le temps de pose pour une étoile plus brillante que la magnitude 3.25 est plus court que 20 s : le temps est majoritairement dépensé à lire le détecteur.
Question 3)
L'observation demande un échantillonnage plus rapide que 3 minutes. Montrer qu'une cible peu brillante ne sera pas observée dans de bonnes conditions. Estimer la limite en magnitude dans le cas où l'on accepte de remplir les pixels à 1/10 de la valeur optimale.
AideSolution
La pose sur l'objet est nécessairement limitée à 160 s.
En application de ce qui précède (avec des pixels bien remplis), une pose de 160 s correspond à la magnitude 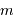 vérifiant
vérifiant
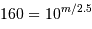 , càd
, càd 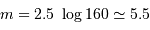 .
.
Le temps de pose pour une étoile moins brillante que la magnitude 5.5 dépasse 160 s.
En acceptant de remplir les pixels de façon très incomplète, le gain d'un facteur 10 en nombre de photoélectrons, donc de photons, correspond à un surcroît de 2.5 magnitudes. La limite en magnitude est donc de l'ordre de 8.

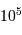 photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.
photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.