Une histoire d'anneaux
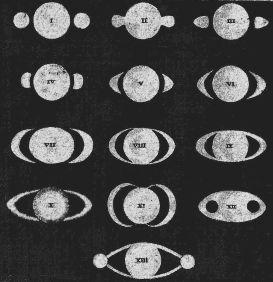
Diverses interprétations rendant compte des observations des anneaux de Saturne
(compilation d'observations de Galilée, Hévélius, Gassendi) : 2 satellites, des protubérances, des anses...
Crédit :
Bibliothèque de l'Observatoire de Paris
Cratères lunaires

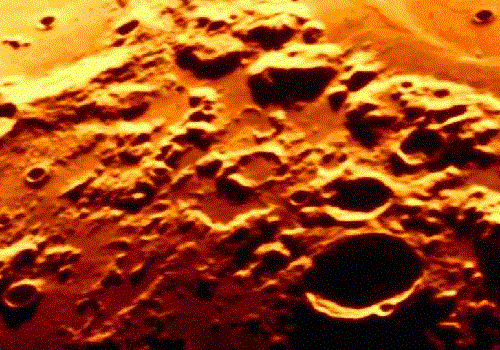
La Lune observée avec une lunette de 70 mm, et avec la caméra grand champ du télescope
CFH.
Crédit :
CFHT
Résolution angulaire et qualité d'image
L'apparence d'un objet dépend intimement de la finesse des détails les plus fins. Ainsi, l'identité des anneaux de Saturne n'a été dévoilée que lorsque des observations de qualité suffisante ont permis de trancher parmi les multiples interprétations alors discutées.
Le gain en résolution angulaire permet une meilleure identification des images ;
par exemple pour la Lune observée avec un petit collecteur, ou bien un grand collecteur corrigé des premiers ordres de la turbulence.
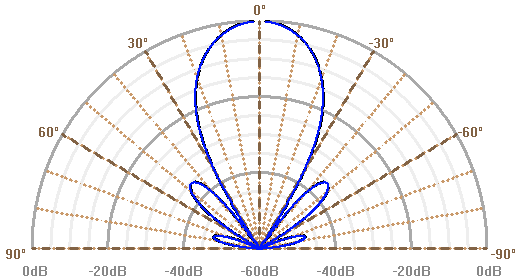
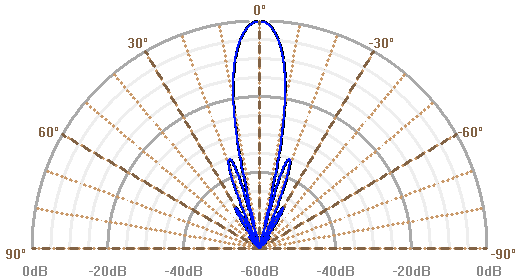
Lobes d'antenne, en diagramme polaire. L'amplitude du lobe est donnée en échelle logarithmique, mesurée en dB d'atténuation par rapport à la réponse dans l'axe.
Crédit :
ASM
Résolution angulaire et longueur d'onde
A grande longueur d'onde, la diffraction empêche une vision spatialement bien résolue, sauf à avoir un collecteur de très grande taille. Pour une antenne radio unique, circulaire de diamètre correspondant à un nombre limité de longueurs d'onde, le lobe d'antenne apparaît très étendu.
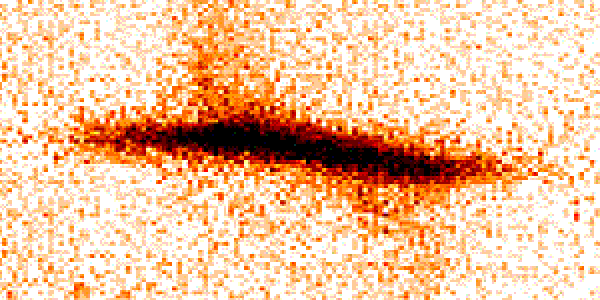
L'objet NGC7782, vu par le spectroimageur UVES du VLT (couleur en vidéo inverse). La pixélisation apparaît clairement.
Crédit :
ESO
Résolution angulaire et taille d'un élément d'image
Il est important, pour enregistrer une image en respectant sa résolution angulaire, d'avoir des éléments d'image ou pixels convenablement dimensionnés.
Vers la haute résolution angulaire
La quête de résolution angulaire de plus en plus fine nécessite des bases de collecte d'observation de plus en plus étendues. Comme la taille d'un élément collecteur est limitée (en 2018 : à 8 m en mono-pupille pour les télescopes du VLT, Gemini Nord et Sud, Subaru ; 10 m en pupille segmentée pour les 2 télescopes Keck; bientôt 39 mètres pour l'ELT européen de l'ESO), on se tourne vers l'interférométrie.
La pixélisation
La résolution angulaire ne dépend pas uniquement des conditions de collecte du signal, avec un collecteur de diamètre plus ou moins grand ; elle dépend aussi de la façon dont l'image est finalement enregistrée.
L'enregistrement du signal, aujourd'hui quasi uniquement sous forme numérique, doit être adapté à la résolution.
Afin que la taille finie des pixels ne limite pas la résolution, le critère de Shannon énonce qu'il faut au moins 2 pixels par élément de résolution.
Par exemple, si la résolution visée est de 0.4", un pixel doit couvrir 0.2".
S'il est plus gros, sa taille va limiter la résolution.
S'il est plus petit, le signal sera suréchantillonné spatialement, sans gain d'information spatiale.
Résolution angulaire variable

Animation montrant l'aspect de la galaxie M31 à diverses résolutions spatiales, balayant les différents aspects avec un appareil très peu résolvant, jusqu'à un bon télescope.
Crédit :
ASM
Résolution angulaire
L'aspect de galaxie M31 (d'Andromède) dépend de la résolution angulaire instrumentale. Plus elle est élevée, plus les détails observables sont fins.
Taille du pixel variable
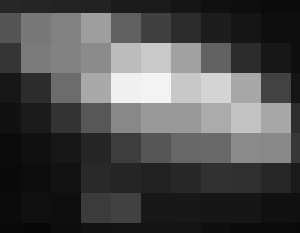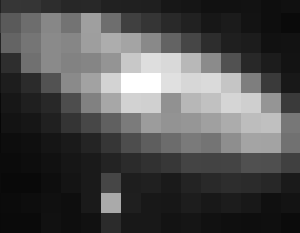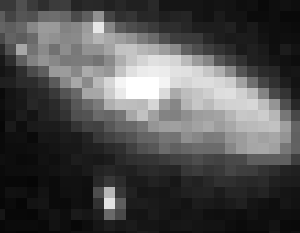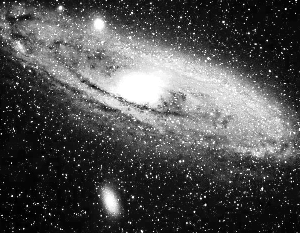
Animation montrant la galaxie M31, à divers niveaux de pixélisation. Plus la taille du
pixel est petite, meilleure est la résolution angulaire, donc la résolution spatiale.
Crédit :
ASM
Résolution angulaire et taille d'un élément d'image
La résolution est également limitée par la pixélisation, qui conditionne la FEP.
 Choix d'une caméra
Choix d'une caméra
Difficulté : ☆
Temps : 20 min
Dans le cadre du développement d'un instrument, on cherche à choisir la caméra optimale, càd celle qui réalisera les performances demandées, pour un coût minimal. Un constructeur propose
des caméras de taille 1k 1k (1000 px par 1000 px), 1k
1k (1000 px par 1000 px), 1k 2k,
2k
2k,
2k 2k, et 2k
2k, et 2k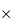 4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
Question 1)
Le collecteur présente un diamètre de 3.6 m, pour une ouverture f/3.3
En déduire la focale équivalente, puis le lien entre la taille physique 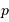 du pixel et le champ
du pixel et le champ 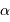 qu'il couvre.
qu'il couvre.
Revoir la relation entre ouverture, focale et diamètre.
Si 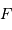 est la focale, alors
est la focale, alors 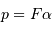
Question 2)
Le champ doit couvrir 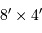 , avec une résolution de
, avec une résolution de 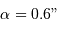 .
En déduire la caméra appropriée.
.
En déduire la caméra appropriée.
Déterminer la taille angulaire d'un pixel.
 Saturne et ses anneaux
Saturne et ses anneaux
Difficulté : ☆☆
Temps : 15 min

Géométrie simplifiée.
Crédit :
ASM
L'identification de la nature des anneaux de Saturne ne fut pas sans peine. Le but de l'exercice est de déterminer la résolution angulaire nécessaire permettant de le faire.
A l'opposition, Saturne s'approche à 8.5 UA de la Terre. Le rayon planétaire vaut 60 000 km, les rayons interne et externe des principaux anneaux respectivement 90 000 et 140 000 km. On suppose que les anneaux sont observés sous grand incidence (l'incidence maximale est de l'ordre de 26 deg), pour être dans un cas favorable (lorsque la Terre passe dans le plan des anneaux... on ne les voit simplement pas). Néanmoins, pour simplifier les calculs, on s'intéresse au seul problème 1-D portant sur la seule variable radiale, selon la géométrie de la figure jointe.
Question 1)
Refaire à l'échelle schéma de Saturne et de ses anneaux. Déterminer le plus petit élément bien contrasté à observer pour pouvoir identifier les anneaux.
[1 points]
Question 2)
La résolution devant être au-moins d'un facteur 2 plus précis que la taille du plus petit élément à identifier, déterminer la résolution nécessaire.
[2 points]
- Question 1
Aide :
Revoir la relation entre ouverture, focale et diamètre.
Aide :
Si 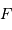 est la focale, alors
est la focale, alors 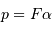
Solution :
Une ouverture de 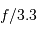 pour un collecteur de 3.6 m représente une focale de
pour un collecteur de 3.6 m représente une focale de
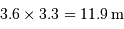 .
.
- Question 2
Aide :
Déterminer la taille angulaire d'un pixel.
Solution :
Bien échantillonner la résolution nécessite un pixel couvrant 0.3" (la moitié de la résolution de 0.6").
Le champ de 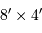 , ou
, ou 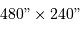 , devient, traduit en pixel,
, devient, traduit en pixel,
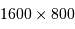 .
.
Avec la focale résultante 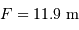 , la résolution de 0.3", cad
, la résolution de 0.3", cad 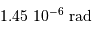 , correspond à une dimension physique de
, correspond à une dimension physique de 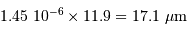 .
.
D'où la caméra choisie : 1k  2k, avec des pixels de
2k, avec des pixels de 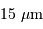 .
.







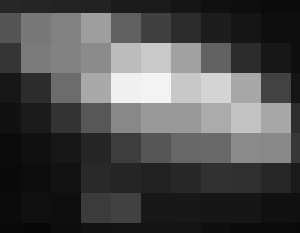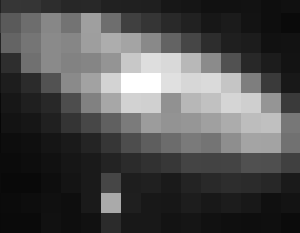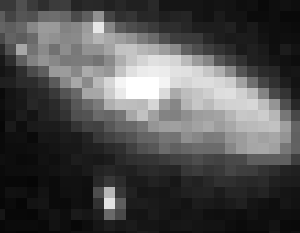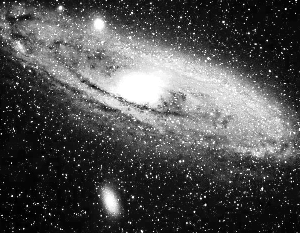
 1k (1000 px par 1000 px), 1k
1k (1000 px par 1000 px), 1k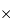 2k,
2k
2k,
2k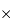 2k, et 2k
2k, et 2k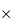 4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
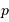 du pixel et le champ
du pixel et le champ 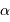 qu'il couvre.
qu'il couvre.
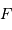 est la focale, alors
est la focale, alors 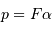
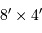 , avec une résolution de
, avec une résolution de 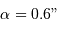 .
En déduire la caméra appropriée.
.
En déduire la caméra appropriée.

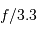 pour un collecteur de 3.6 m représente une focale de
pour un collecteur de 3.6 m représente une focale de
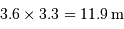 .
.
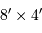 , ou
, ou 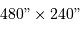 , devient, traduit en pixel,
, devient, traduit en pixel,
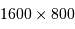 .
.
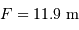 , la résolution de 0.3", cad
, la résolution de 0.3", cad 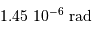 , correspond à une dimension physique de
, correspond à une dimension physique de 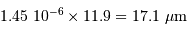 .
.
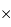 2k, avec des pixels de
2k, avec des pixels de 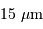 .
.