Les éclipses de Lune
Auteur: P. Rocher - IMCCE- Observatoire de Paris
- Introduction
- La géometrie des éclipses de Lune
- Introduction
- Le cône d'ombre et le cône de pénombre
- Les différents types d'éclipses de Lune
- Caractéristiques des cônes d'ombre et de pénombre
- Les effets géométriques de l'atmosphère terrestre
- Les effets lumineux de l'atmosphère terrestre
- Grandeur d'une éclipse de Lune
- Les données fournies pour une éclipse de Lune
- En savoir plus: Exemple de données
- Zones de visibilité d'une éclipse de Lune
- En savoir plus: Carte de visibilité de l'éclipse totale du 4 mai 2002
- Quand ont lieu les éclipses de Lune ?
- Introduction
- Le mouvement moyen de la ligne des noeuds
- En savoir plus: Le calcul de la saison des éclipses
- En savoir plus: Le mouvement réel de la ligne des noeuds
- Le critère en latitude
- En savoir plus: La démonstration du critère en latitude
- En savoir plus: La démonstration du critère en latitude-2
- Le critère en longitude
- Nombre d'éclipses à chaque saison d'éclipse
- Nombre d'éclipses par an
- Les séries courtes d'éclipses
- Répartition des éclipses sur une période de 22 ans
- Canons et grandeurs des éclipses de Lune
- Introduction
- Grandeurs des éclipses de Lune
- Les canons d'éclipses de Lune
- En savoir plus: Le canon de l'IMCCE
- Les éclipses totales les plus longues
- Les éclipses totales les plus grandes
- Les éclipses les plus faibles et les plus courtes
- Le Saros et les suites longues d'éclipses de Lune
- Introduction
- Nombre d'éclipses dans un Saros
- Eclipses homologues et suites longues d'éclipses de Lune
- Evolutions des éclipses homologues
- En savoir plus: Positions des éclipses d'une saison éclipse
- Evolutions des suites homologues - suite
- En savoir plus: Exemple de Saros
- Les éclipses anciennes
- Introduction
- Visibilité des éclipses anciennes à l'oeil nu
- Quelques éclipses historiques
- Rotondité de la Terre
- Le calcul de la distance Terre-Lune
- Introduction
- Par Aristarque de Samos
- En savoir plus: Une des démonstrations d'Aristarque
- Par Claude Ptolémée
Introduction
 Introduction
Introduction
Ce chapitre porte sur les éclipses de Lune, nous allons reprendre une étude analogue à celle faite pour les éclipses de Soleil. Une grande partie des notions nécessaires pour cette étude a donc été développée dans les chapitres sur les éclipses de Soleil : le mouvement de la Terre, le mouvement de la Lune, les révolutions tropique, synodique, draconitique et anomaslistique, la notion de saison d'éclipses et de Saros. Nous insisterons particulièrement sur les différences entre les deux types d'éclipses.
 Prérequis
Prérequis
Il est vivement conseillé de lire le cours sur les mouvement de la Terre et de la Lune.
La géometrie des éclipses de Lune
Introduction
 Introduction
Introduction
Dans cette section, nous abordons l'aspect géométrique des éclipses de Lune : la taille des cônes d'ombre et de pénombre de la Terre au niveau de l'orbite lunaire. Puis nous définissons les différents types d'éclipses de Lune, les caractéristiques des cônes d'ombres et de pénombres, les effets géométriques et lumineux de l'athmosphère terrestre. Nous donnons ensuite la définition de la grandeur d'une éclipse de Lune et nous présentons les différents paramètres figurant dans les prédictions d'éclipse de Lune (avec un exemple). Nous terminons en présentant les zones de visibilité des éclipses de Lune et leurs représentations sur une carte en projection de Mercator.
Le cône d'ombre et le cône de pénombre
La Terre, éclairée par le Soleil, donne naissance, dans la direction opposée au Soleil à deux cônes, un cône d'ombre et un cône de pénombre. La droite joignant le centre du Soleil et le centre de la Terre constitue l'axe de ces cônes. Le sommet Sp du cône de pénombre est situé sur cet axe entre le Soleil et la Terre, et le sommet So du cône d'ombre est également situé sur cet axe mais de l'autre côté par rapport à la Terre. Le cône d'ombre est construit à l'aide des tangentes extérieures aux sphères solaire et terrestre, le cône de pénombre est construit à partir des tangentes intérieures aux sphères solaire et terrestre.
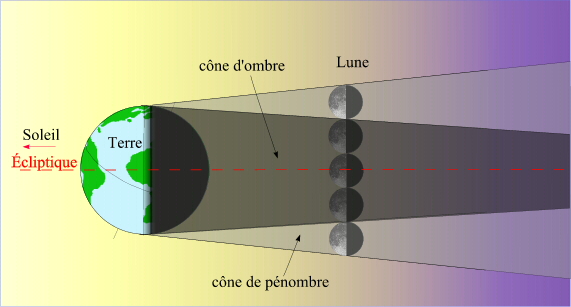
Cônes d'ombre et de pénombre.
Crédit : IMCCE/Patrick Rocher
La distance entre le sommet du cône d'ombre et le centre de la Terre varie en fonction de la distance Terre-Soleil. Elle est maximale, environ 231 rayons terrestres, lorsque la Terre est à son aphélie (actuellement vers le 4 juillet). Elle est minimale, environ 221 rayons terrestres, lorsque la Terre est à son périhélie (actuellement vers le 4 janvier). La Terre étant environ quatre fois plus large que la Lune, son ombre est également quatre fois plus longue. En cas d'éclipse de Lune, la Lune traverse le cône d'ombre terrestre au quart de sa longueur depuis la Terre, car la longueur Terre-Lune est égale à la longueur du cône d'ombre de la Lune. En cet endroit la largeur de la section du cône d'ombre de la Terre est de l'ordre des trois quarts de sa base, donc des trois quarts du diamètre terrestre, soit environ trois disques lunaires comme indiqué sur la figure ci-dessus.
De même la taille de la largeur de la couronne de pénombre de la Terre, à l'endroit où elle est traversée par la Lune est simple à évaluer. En effet, comme on le voit sur la figure ci-dessous c'est la largeur de la Lune elle-même, l'angle p des tangentes sud est égal au diamètre apparent du Soleil, qui est lui-même presque égal au diamètre apparent de la Lune. Donc une éclipse de Lune par la pénombre peut être totale.
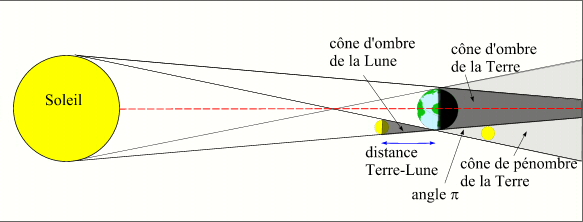
Cônes d'ombre et de pénombre.
Crédit : IMCCE/Patrick Rocher
 Remarque
Remarque
Sur cette figure les proportions ne sont pas respectées, le Soleil devrait être 400 fois plus gros que la Lune et 400 fois plus loin.
Les différents types d'éclipses de Lune
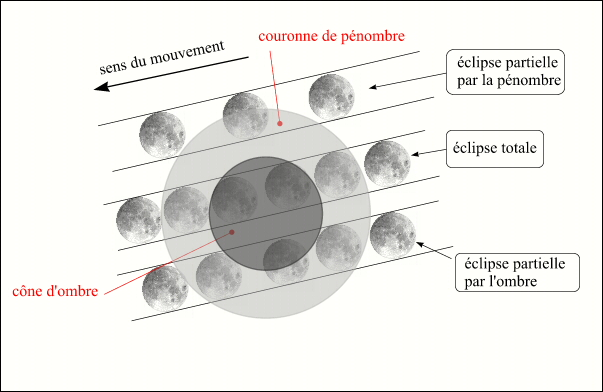
Les différents types d'éclipses de Lune
Crédit : IMCCE/Patrick Rocher
Comme nous l'avons vu précédemment, la section du cône d'ombre au niveau de l'orbite de la Lune est largement supérieure au diamètre apparent de la Lune (environ trois diamètres lunaires), la Lune peut donc être totalement éclipsée par l'ombre de la Terre, dans ce cas l'éclipse de Lune est dite totale.
Lorsqu'une partie seulement de la Lune passe dans le cône d'ombre de la Terre, la Lune n'est que partiellement éclipsée, l'éclipse est dite partielle par l'ombre.
Nous avons vu également que la taille de la couronne de pénombre était de la taille du diamètre apparent du Soleil et pouvait être supérieure au diamètre apparent de la Lune (Terre au périhélie et Lune à l'apogée). Dans ce cas la Lune peut passer entièrement dans la couronne de pénombre, dans ce cas l'éclipse de Lune est dite totale par la pénombre. Lorsque la Lune passe partiellement dans la couronne de pénombre il y a éclipse partielle de la Lune par la pénombre.
Caractéristiques des cônes d'ombre et de pénombre
Comme nous l'avons déjà vu la distance entre le centre de la Terre et le sommet du cône d'ombre et donc sa largeur varie en fonction de la distance Terre-Soleil. Elle vaut environ 231 rayons terrestres lorsque la Terre est à l'aphélie et elle vaut 221 rayons terrestres lorsque la Terre est à son périhélie.
De même la distance entre le sommet du cône de pénombre et le centre de la Terre dépend de la distance Terre-Soleil, elle est maximale, environ 216 rayons terrestres lorsque la Terre est à son aphélie et elle est minimale, environ 209 rayons terrestres lorsque la Terre est à son périhélie.
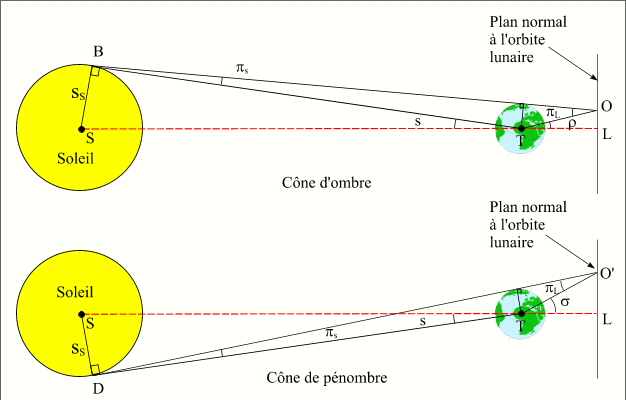
Demi-diamètres apparents géocentriques de l'ombre et de la pénombre
Crédit : IMCCE/Patrick Rocher
Sur la figure ci-dessus le demi-diamètre apparent géocentrique de la section de l'ombre de la Terre par le plan normal à l'orbite lunaire est égal à l'angle ρ. L'ombre est déterminée par le cône de révolution d'axe ST et de génératrice BO, tangente extérieure au Soleil et à la Terre. Dans le triangle TOB la somme des angles intérieurs πs et πL est égale à la somme des angles extérieurs s et ρ. Or par définition πs est la parallaxe horizontale du Soleil, πL la parallaxe horizontale de la Lune et sS est le demi-diamètre apparent du Soleil. Donc ρ est égale à πs + πL - sS.
Ce demi-diamètre ρ est donc maximal lorsque la parallaxe lunaire πL est maximale et le demi-diamètre apparent πs est minimal (la parallaxe πs du Soleil étant pratiquement constante), c'est-à-dire lorsque la Lune est à son périgée et lorsque la Terre est à son aphélie. De même ce demi-diamètre ρ est minimal lorsque la parallaxe lunaire est minimale et le demi-diamètre apparent du Soleil est maximal, c'est-à-dire lorsque la Lune est à son apogée et la Terre à son périhélie.
On peut faire un raisonnement analogue pour le calcul du demi-diamètre apparent géocentrique du cône de pénombre σ. On trouve que σ est égal à πs + πL + sS. Ce demi-diamètre σ est donc maximal lorsque πL et sS sont maximales, donc lorsque la Lune est à son périgée et la Terre à son périhélie et il est minimal lorsque πL et sS sont minimales, donc lorsque la Lune est à son apogée et la Terre à son aphélie.
On remarquera que la largeur de la couronne de pénombre σ - ρ est bien égale au diamètre apparent du Soleil (2sS)
Le tableau suivant donne les valeurs extrêmes et moyennes du demi-diamètre sS apparent du Soleil, de la parallaxe lunaire πL et du demi-diamètre apparent sL de la Lune.
|
Terre périhélie
|
Moyenne
|
Terre aphélie
|
| sS
|
16'18" |
15'59.63" |
15'46" |
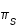
|
8.96" |
8.80" |
8.65" |
|
Lune périgée
|
Moyenne
|
Lune apogée
|
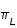
|
61' 27" |
57' 02,7" |
53' 53" |
| sL
|
16' 45" |
15' 32, 58" |
14' 41" |
Le tableau suivant donne les valeurs extrêmes et moyennes des demi-diamètres apparents géocentriques du cône d'ombre et du cône de pénombre.
|
Minimal |
Moyen |
Maximal |
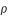
|
2263,96" = 37' 43,96" = 2,57 sL
|
2471,87" = 41' 11,87" = 2,65sL
|
2749,66" = 45' 49,66" = 2,74 sL
|
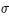
|
4187,65" = 1°09' 47,65" = 4,75 sL
|
4391,13" = 1° 13' 11,13" = 4,71 sL
|
4673,96" = 1° 17' 53,96" = 4,65 sL
|
On va voir que ces quantités doivent être augmentées de 1/73 en valeur relative pour ρ et de 1/128 en valeur relative pour σ afin de tenir compte de l'atmosphère terrestre.
Les effets géométriques de l'atmosphère terrestre
Contrairement aux éclipses de Soleil où l'ombre et la pénombre sont générées par un astre sans atmosphère, dans le cas des éclipses de Lune nous devons tenir compte des effets de l'atmosphère terrestre dans les calculs des limites de l'ombre et de la pénombre de la Terre.
Le trajet géométrique des rayons lumineux est soumis à la réfraction atmosphérique. L'atmosphère terrestre n'a pas de limite déterminée, on adopte une limite supérieure pour laquelle la réfraction atmosphérique n'a plus d'effets sensibles. Notre connaissance actuelle des répartitions des densités dans l'atmosphère suivant la verticale, ainsi que des mesures effectives de l'ombre de la Terre durant des éclipses de Lune nous conduisent à prendre 75km pour valeur limite. Cela se traduit dans les calculs par une augmentation du rayon terrestre de 1/85 en valeur relative. D'autre part la parallaxe de la Lune doit être une valeur moyenne et non pas la parallaxe horizontale, on prend donc la parallaxe lunaire à 45° de latitude, donc dans les calculs cela se traduit par une diminution de la parallaxe lunaire de 1/594 en valeur relative. Si l'on tient compte de ces deux corrections la valeur de la parallaxe horizontale doit être systématiquement augmentée de 1%. Cela se traduit par une augmentation du demi-diamètre géocentrique apparent ρ de l'ombre de 1/73 et une augmentation du demi-diamètre géocentrique σ apparent de la pénombre de 1/128.
Connaissant la valeur de la réfraction à l'horizon (environ 35') on peut calculer la distance du sommet cône d'ombre minimal, dans lequel on est sûr qu'il n'y aura aucune lumière solaire réfractée. On trouve une distance géocentrique du sommet de ce cône égale à environ 40 rayons terrestres. La distance Terre-Lune variant entre 56 et 63,8 rayons terrestres on est certain que la Lune recevra toujours des rayons solaires réfractés par l'atmosphère.
Les effets lumineux de l'atmosphère terrestre
L'atténuation atmosphérique
Comme nous venons de le voir, en raison de la réfraction et des distances Terre-Lune, la Lune éclipsée reçoit toujours des rayons lumineux réfractés par l'atmosphère terrestre.
La réfraction est également la cause d'un phénomène d'atténuation, dans la figure ci-dessous, considérons un rayon lumineux élémentaire, d'angle d
τ, issue du point S du disque solaire considéré plan (1). Ce rayon, suite à la réfraction atmosphérique, va illuminer la surface dS' située dans le plan de la Lune (2). En absence de réfraction il illuminerait la surface dS. Dans les deux cas le flux de lumière qui illumine ces deux surfaces est le même, les surfaces n'étant pas égales, la surface dS', supérieure à dS est moins éclairée.
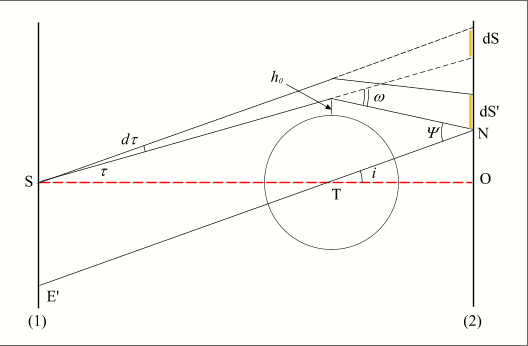
Crédit : IMCCE/Patrick Rocher
L'atténuation est donnée par le rapport des surfaces dS/dS' = Φ-1
Le terme Φ peut s'écrire sous la forme suivante :
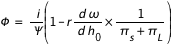
Cette formule comporte deux facteurs qui agissent en sens inverse, le premier diminue la surface éclairée (ds) et le deuxième élargit la surface éclairée (dS'), la combinaison des deux crée l'atténuation par réfraction. Pour imager notre propos considérons la figure suivante dans laquelle un rayon cylindrique de largeur dS est réfracté suivant une surface (ds) plus petite si on considère que la réfraction ne varie pas avec l'altitude (premier terme de la formule) et qui est réfracté suivant dS' si on considère que la réfraction décroît avec l'altitude (deuxième terme de la formule). Le premier terme fait donc bien croître l'illumination et le second la fait décroître.
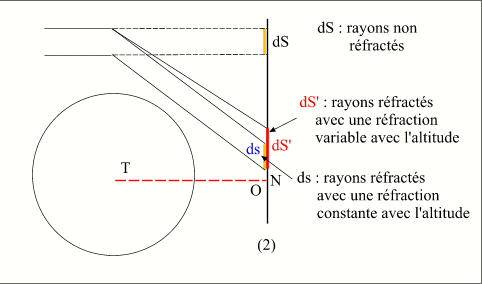
Crédit : IMCCE/Patrick Rocher
Si l'on exprime les variations de Φ en fonction de l'altitude h dans l'atmosphère, on s'aperçoit que c'est dans la haute atmosphère (troposphère) que l'atténuation est la plus appréciable malgré la faible valeur de la réfraction. Elle décroît ensuite jusqu'à la valeur un, pour une altitude h d'environ 2km, puis le phénomène s'amplifie et pour la valeur i=0 il y a focalisation. De plus on peut dire que l'atténuation par la réfraction est pratiquement neutre et que l'ombre est approximativement grise.
L'absorption atmosphérique
L'absorption atmosphérique est produite par la diffusion de la lumière par les molécules et les aérosols de l'air. L'absorption atmosphérique est très sensible à la longueur d'onde (c'est une loi en 1/λ
4). La lumière bleue est donc plus absorbée que la lumière rouge, cette absorption croît avec la largeur de la couche atmosphérique traversée, ce qui explique le rougeoiement du ciel au coucher du Soleil. Dans le cas des éclipses de Lune ce sont les rayons passant à faible altitude qui traversent la plus grande largeur d'atmosphère, ce sont donc ces rayons qui ont un maximum de lumière bleue absorbée et qui sont donc les plus rouges. Comme ce sont aussi ces rayons qui sont les plus réfractés, le centre de l'ombre aura un aspect rougeâtre.
Le degré d'absorption dépend également des conditions météorologiques, donc la luminosité de la partie centrale de l'ombre est très sensible aux conditions météorologiques régnant dans les couches atmosphériques traversées.
L'intensité lumineuse au centre du cône dépend également de la distance à laquelle se trouve la Lune, et les éclipses totales proches du périgée sont toujours plus sombres que les éclipses totales proches de l'apogée.
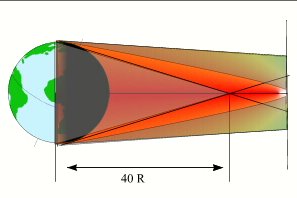
Limite des rayons réfractés
Crédit : IMCCE/Patrick Rocher
Grandeur d'une éclipse de Lune
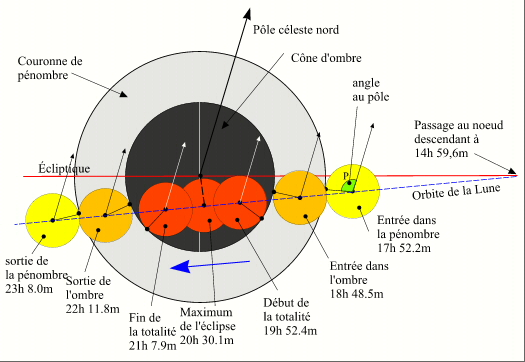
La grandeur, ou magnitude, est un paramètre important des éclipses de Lune. Dans le cas des éclipses totales et partielles par l'ombre, elle est égale au rapport de la distance du bord de la Lune (A) le plus proche du centre du cône d'ombre au bord du cône d'ombre le plus près du centre de la Lune (B) sur le diamètre de la Lune (AC) et cela à l'instant du maximum de l'éclipse, c'est-à-dire à l'instant où la distance entre le centre de la Lune et le centre de l'ombre est minimale. Pour une éclipse par la pénombre la définition de la grandeur est identique, il suffit de remplacer le cône d'ombre par le cône de pénombre.
Dans le cas d'une éclipse par l'ombre on a : 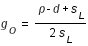
et dans le cas d'une éclipse par la pénombre on a 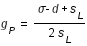
où d est la distance entre le centre de la Lune et le centre de l'ombre, sL le demi-diamètre lunaire, ρ et σ étant respectivement les demi-diamètres apparents de l'ombre et de la pénombre.
Compte tenu de cette définition, plus la grandeur d'une éclipse est importante plus la Lune passe près du centre du cône d'ombre. Les éclipses totales par l'ombre ou par la pénombre ont une grandeur supérieure à un et les éclipses partielles ont une grandeur inférieure à un. La grandeur d'une éclipse totale centrale est égale à 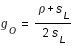 .
.
Grandeur des éclipses de Lune.
Crédit : IMCCE/Patrick Rocher
Sur le dessin ci-dessus, pour les éclipses par la pénombre B est l'intersection de Ox avec le bord de la pénombre. Pour les éclipses partielles et les éclipses totales B est l'intersection de Ox avec le bord de l'ombre. AC est le diamètre lunaire (2sL).
Les données fournies pour une éclipse de Lune
Pour chaque éclipse de Lune, on donne les instants des débuts et des fins des différentes phases. Ces instants, exprimés en Temps universel coordonné, sont les mêmes quel que soit le lieu d'observation, la visibilité des différentes phases est uniquement liée au fait que la Lune soit levée ou non aux instants considérés. On donne également la valeur de la grandeur de l'éclipse, parfois appelée magnitude.
Les différentes phases des éclipses de Lune sont les suivantes :
- L'entrée de la Lune dans la pénombre : c'est l'instant où le disque lunaire est tangent extérieur au cône de pénombre.
- L'entrée de la Lune dans l'ombre, uniquement les éclipses par l'ombre : c'est l'instant où le disque lunaire est tangent extérieur au cône d'ombre.
- Le commencement de la totalité, uniquement pour les éclipses totales par l'ombre : c'est l'instant où le disque lunaire est tangent intérieur au cône d'ombre.
- Le maximum de l'éclipse : c'est l'instant où la distance entre le centre du disque lunaire et le centre du cône d'ombre est minimale.
- La fin de la totalité, uniquement pour les éclipses totales par l'ombre : c'est l'instant où le disque lunaire est de nouveau tangent intérieur au cône d'ombre.
- La sortie de l'ombre, uniquement pour les éclipses par l'ombre : c'est l'instant où le disque lunaire est de nouveau tangent extérieur avec le cône d'ombre.
- La sortie de la pénombre : c'est l'instant où le disque lunaire est de nouveau tangent extérieur avec le cône de pénombre.
Pour chaque début et fin de phase on donne également l'angle au pôle des points de contacts, les points de contacts sont les points de tangences entre le disque lunaire et les cônes d'ombre et de pénombre. L'angle au pôle est l'angle formé par la direction du pôle nord céleste et la demi-droite issue du centre lunaire et passant par le point de tangence, cet angle est compté positivement vers l'ouest (donc dans le sens direct).
On fournit également avec ces valeurs les durées des différentes phases de l'éclipse.
- La durée totale de l'éclipse : intervalle de temps entre l'entrée et la sortie de la pénombre.
- La durée de la phase partielle : intervalle de temps entre l'entrée et la sortie de l'ombre.
- La durée de la totalité : intervalle de temps entre le début et la fin de la totalité.
On donne également les positions apparentes géocentriques du centre de l'ombre et du centre de la Lune pour l'instant du maximum de l'éclipse, ainsi que les valeurs de certains paramètres géométriques de l'éclipse.
- L'ascension droite géocentrique apparente du centre de l'ombre.
- La déclinaison géocentrique apparente du centre de l'ombre.
- Le diamètre apparent du cône d'ombre.
- Le diamètre apparent du cône de pénombre.
- La parallaxe équatoriale du Soleil.
- L'ascension droite géocentrique apparente du centre de la Lune.
- La déclinaison géocentrique apparente du centre de la Lune.
- Le diamètre apparent de la Lune.
- La parallaxe équatoriale de la Lune.
En savoir plus: Exemple de données
 En savoir plus: L'éclipse totale de Lune du 4 mai 2004
En savoir plus: L'éclipse totale de Lune du 4 mai 2004
Éléments à l'instant du maximum de l'éclipse
- Maximum de l'éclipse le 4 mai 2004 à 20h 30m 7,031s UTC
- Ascension droite du centre de l'ombre : 14h 48m 55,84s.
- Déclinaison du centre de l'ombre : -16° 14' 51,48".
- Diamètre du cône d'ombre : 91,16'
- Diamètre du cône de pénombre : 154,59'
- Parallaxe équatoriale du Soleil : 8,72".
- Ascension droite du centre de la Lune : 14h 48m 25,15s.
- Déclinaison du centre de la Lune : -16° 32' 22,88".
- Diamètre apparent de la Lune : 33,07'
- Parallaxe équatoriale de la Lune : + 1° 0' 40,81".
Circonstance de l'éclipse
| Phases |
Instant en UTC |
Longitude* |
Latitude* |
Angle au pôle |
| Entrée dans la pénombre |
le 4 à 17h 52,2m |
-89° 32,4' |
-15° 54,5' |
101,1° |
| Entrée dans l'ombre |
le 4 à 18h 48,5m |
-75° 58,7' |
-16° 8,1' |
95,0° |
| Début de la totalité |
le 4 à 19h 52,4m |
-60° 36,1' |
-16° 23,4' |
251,9° |
| Maximum de l'éclipse |
le 4 à 20h 30,1m |
-51° 31,1' |
-16° 32,4' |
202,8° |
| Fin de la totalité |
le 4 à 21h 7,9m |
-42° 25,9' |
-16° 41,3' |
153,6° |
| Sortie de l'ombre |
le 4 à 22h 11,8m |
-27° 3,5' |
-16° 56,4' |
310,6° |
| Sortie de la pénombre |
le 4 à 23h 8,0m |
-13° 31,3' |
-17° 9,5' |
304,4° |
(*) Dans ce tableau les longitudes et latitudes sont les coordonnées des lieux ayant la Lune au zénith à chaque phase, les longitudes sont comptées positivement vers l'ouest et négativement vers l'est.
On donne également la durée des différentes phases :
- Durée de l'éclipse : 5h 15m 50,50s.
- Durée de la phase partielle : 3h 23m 15,05s.
- Durée de la phase totale : 1h 15m 29,43s.
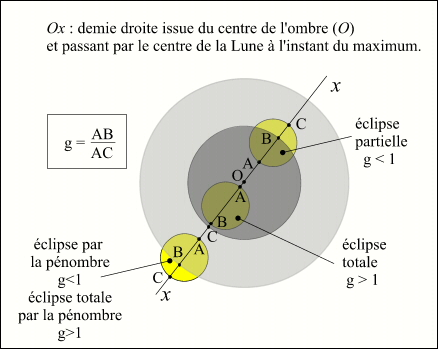
Phases de l'éclipse totale de Lune du 4 mai 2004.
Crédit : IMCCE/Patrick Rocher
Les éphémérides de la Lune donnent les renseignements supplémentaires suivants :
- le 04/05/2004 à 09h 19m 04s UT : la Lune entre dans la constellation de la Balance.
- le 04/05/2004 à 14h 59m 39s UT : la Lune passe par le nœud descendant de son orbite, long. moyenne = +221° 15,7'.
- le 04/05/2004 à 20h 33m 24s UT : Pleine Lune.
- le 06/05/2004 à 04h 31m 56s UT : la Lune au périgée (distance minimale à la Terre) d=359811 km, diam. app. =33.3'.
On constate que la Lune est passée par le nœud descendant de son orbite avant le début de l'éclipse, c'est donc une éclipse au nœud descendant, donc logiquement le maximum de l'éclipse, correspondant à la distance minimale du centre du disque lunaire au centre de l'ombre doit avoir lieu avant l'opposition (pleine Lune). Ce qui est bien le cas le maximum a lieu à 20h 30.1m et la pleine Lune a lieu à 20h 33,6m. De plus on constate que la Lune est proche de son périgée, donc sa vitesse angulaire est forte et son diamètre apparent est proche de son maximum. Donc la durée de l'éclipse est relativement courte (proche de 5h).
Zones de visibilité d'une éclipse de Lune
Comme nous l'avons déjà dit, pour qu'une éclipse de Lune soit visible en un lieu donné, il suffit que la Lune soit levée en ce lieu durant l'éclipse. La durée totale d'une éclipse pouvant atteindre plusieurs heures il y a obligatoirement des parties du globe terrestre qui ne verront qu'une partie de l'éclipse. Pour connaître les différents endroits du globe où une éclipse de Lune est visible, il suffit de tracer sur une carte les lieux où la Lune est à l'horizon à l'instant des débuts et des fins des différentes phases de l'éclipse. Sur ces courbes, une première moitié des lieux correspond à un lever de Lune et une seconde moitié des lieux correspond à un coucher de Lune. Tous les points du globe situés à l'est de la première moitié et à l'ouest de la seconde voient la Lune et donc la phase de l'éclipse correspondant.
Au maximum, il y a trois débuts et trois fins de phase pour une éclipse, on trace donc au plus six courbes de visibilité par éclipse et l'on utilise les notations suivantes :
- P1 : la limite de la région où l'on observe l'entrée dans la pénombre (pointillés larges),
- O1 : la limite de la région où l'on observe l'entrée dans l'ombre (pointillés normaux),
- T1 : la limite de la région où l'on observe l'entrée dans la totalité (petits pointillés),
- T2 : la limite de la région où l'on observe la fin de la totalité (petits pointillés),
- O2 : la limite de la région où l'on observe la sortie de l'ombre (pointillés normaux),
- P2 : la limite de la région où l'on observe la sortie de la pénombre (pointillés larges),
- V : la région de visibilité,
- I : la région d'invisibilité.
La lettre V indique la portion du globe terrestre où l'éclipse est visible (en totalité ou en partie) et la lettre I indique la portion du globe où l'éclipse n'est pas visible.
On utilise généralement une projection de Mercator, on s'arrange pour centrer la carte sur la zone de visibilité V de l'éclipse. Par exemple tous les lieux situés à l'intérieure de la courbe P1 contenant le symbole V voient l'entrée de la Lune dans la pénombre.
 Remarque
Remarque
Chaque courbe est le terminateur du lieu où la Lune est au zénith pour chaque début ou fin de phase, c'est pourquoi on fournit avec chaque instant correspondant aux débuts et aux fins de phase les coordonnées géographiques du lieu ayant la Lune au zénith, ces coordonnées permettent de tracer sur les cartes les terminateurs en question, c'est-à-dire les grands cercles de la sphère terrestre ayant pour pôles ces lieux.
En savoir plus: Carte de visibilité de l'éclipse totale du 4 mai 2002
 En savoir plus
En savoir plus
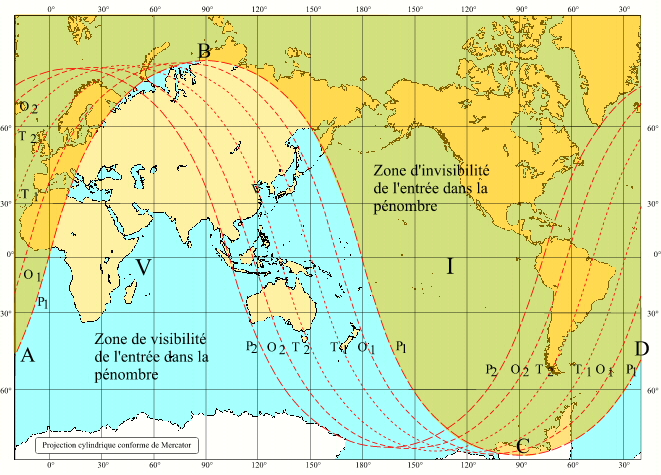
Carte de visibilité de l'éclipse totale de Lune du 4 mai 2002
Crédit : IMCCE/Patrick Rocher
Sur cette carte P1 indique les lieux où la Lune est à l'horizon au début de l'éclipse (entrée dans le cône de pénombre), la partie gauche AB et extrême droite CD de la courbe correspondent au lever de la Lune et la partie centrale BC de la courbe correspond au coucher de la Lune. Les lieux situés dans la zone de visibilité, en claire sur la carte verront le début de l'éclipse, les lieux de la partie ombrée ne verront pas le début de l'éclipse. On peut faire un raisonnement identique pour chacune des cinq autres courbes.
Explication de la visibilité de l'éclipse à Paris
Paris est à l'ouest des parties des courbes P1 et O1 correspondant au lever de la Lune aux instants des entrées dans la pénombre et dans l'ombre, on ne verra donc pas ces deux débuts de phase à Paris car la Lune n'y sera pas levée. Par contre Paris est à l'est de toutes les autres courbes, dont on verra toutes les autres phases de l'éclipse : ainsi la Lune se lèvera partiellement éclipsée par l'ombre de la Terre, puis on verra le début de la totalité, puis toute la phase totale puis la fin de la totalité et en fin les sorties de l'ombre et de la pénombre. On peut vérifier très simplement cette prédiction en comparant les instants des différentes phases de l'éclipse avec les heures du lever du Soleil à Paris ce jour. En effet comme nous sommes proches de la pleine Lune, la Lune se lève sensiblement lorsque le Soleil se couche vers 19h 9min UTC, or les deux premières phases qui débutent respectivement à 17h 52.2m UTC et à 18h 48.5m UTC ne seront effectivement pas visibles, par contre l'entrée dans l'ombre ayant lieu à 19h 52.4m UCT sera visible car la Lune sera levée. Les phases suivantes, jusqu'à la dernière phase (sortie de la pénombre) qui aura lieu à 23h 8m UTC donc en pleine nuit, seront visibles.
En conclusion on peut dire que pour connaître la visibilité d'une éclipse de Lune en un lieu quelconque il suffit de comparer les instants des différentes phases de l'éclipse avec les heures de nuit en ce lieu. Toutes les phases ayant lieu de nuit sont visibles.
Quand ont lieu les éclipses de Lune ?
Introduction
 Introduction
Introduction
Dans cette section nous abordons l'aspect dynamique des éclipses de Lune. Nous reparlons du mouvement de la ligne des noeuds de l'orbite lunaire et de la saison des éclipses, nous définissons de nouveau des critères en latitude et en longitude pour avoir une éclipse au voisinage de la pleine Lune. Nous étudions, comme pour les éclipses de Soleil, le nombre d'éclipses à chaque saison d'éclipse et l'évolution des éclipses saison après saison. Nous reprenons la prédiction des éclipses de Lune et de Soleil sur la période de 22 ans (1998-2020).
Le mouvement moyen de la ligne des noeuds
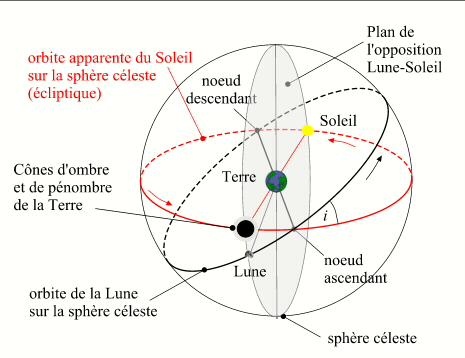
Opposition de la Lune et du Soleil : pleine Lune
Crédit : IMCCE/Patrick Rocher
Il y a éclipse de Lune lorsque la Lune passe dans le cône d'ombre ou dans le cône de pénombre de la Terre. Le Soleil, la Terre et la Lune sont alors presque alignés, et on est au voisinage de la pleine Lune (opposition). Si le plan de l'orbite de la Lune était le même que le plan de l'orbite de la Terre (écliptique), il y aurait une éclipse de Lune à chaque pleine Lune, or le plan de l'orbite de la Lune est incliné d'environ 5° 17' sur le plan de l'orbite terrestre à la pleine Lune. À chaque instant, l'intersection de ces deux plans est une droite appelée ligne des nœuds et les intersections de cette droite avec l'orbite de la Lune sont appelées nœuds de l'orbite lunaire.
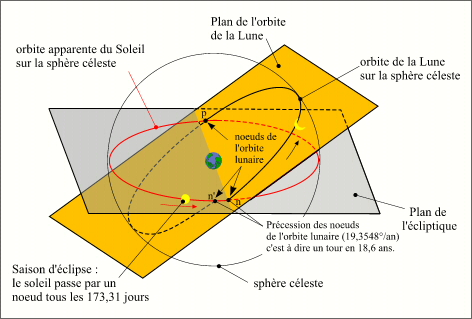
Orbites de la Lune, mouvement de la ligne des nœuds
Crédit : IMCCE/Patrick Rocher
Cette ligne des nœuds n'est pas fixe, elle est animée, dans le sens rétrograde (sens des aiguilles d'une montre), d'un mouvement de précession d'une période de 18,6 ans, soit un déplacement de 19,354 8° par an.
Pour qu'il y ait une éclipse il faut donc, dans le repère écliptique géocentrique, que la direction Soleil-Terre soit près de la ligne des nœuds lunaires au moment de la pleine Lune. Compte tenu du mouvement de précession des nœuds, le Soleil apparent passe par l'un des deux nœuds tous les 173,31 jours. Cette période porte le nom de saison d'éclipses. Il passe par le même nœud tous les 346,32 jours, cette période porte le nom d'année des éclipses.
En savoir plus: Le calcul de la saison des éclipses
 En savoir plus
En savoir plus
La direction Terre-Soleil est la direction du Soleil apparent vu depuis la Terre, elle fait donc 360° pendant une révolution sidérale de la Terre. La ligne des nœuds de l'orbite lunaire se déplace en moyenne de 19,3413618°/an dans le sens rétrograde. On a donc deux mouvements en sens contraire. La période T qui ramène le Soleil apparent dans la direction d'un même nœud de l'orbite lunaire est solution de l'équation suivante :
T . 360°/an + T . 19,3413618°/an = 360°
ce qui donne T = 360/(360 + 19,3413618) an = 0,9490133 an.
L'année sidérale étant égale à : an = 365,2563632 jours, T = 346,63 jours.
La saison des éclipses correspond à l'intervalle de temps mis par le Soleil apparent pour passer d'un nœud de l'orbite lunaire à l'autre, elle est donc égale à T/2 ~ 173,31 jours.
La valeur de cette période T nous permet de calculer la vitesse moyenne du Soleil apparent (ou de la Terre) dans un repère tournant lié à la ligne des nœuds de l'orbite lunaire. Par rapport à cette ligne des nœuds le Soleil apparent fait un tour de 360° en 346,63 jours, sa vitesse moyenne par rapport à la ligne des nœuds est donc de 360°/346,63j = 1,038°/jour.
En savoir plus: Le mouvement réel de la ligne des noeuds
 En savoir plus
En savoir plus
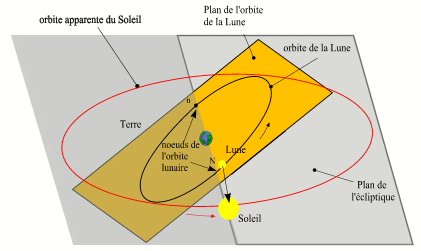
Système Terre - Lune - Soleil lorsque le Soleil est sur la ligne des nœuds
Crédit : IMCCE/Patrick Rocher
En réalité, le mouvement rétrograde de la ligne des nœuds présente des inégalités importantes. À certaines époques, sa vitesse est le double de la moyenne. À d'autres moments, sa vitesse est nulle, les nœuds sont alors stationnaires. Cela se produit aux voisinages du passage du Soleil dans la direction de la ligne des nœuds, donc au voisinage des éclipses de Soleil (et aussi de Lune). On peut expliquer ce phénomène de la manière suivante, lorsque le Soleil est sur la ligne des nœuds, il se trouve dans le plan de l'orbite de la Lune, la force perturbatrice du Soleil est alors comprise dans le plan de l'orbite de la Lune, donc la composante perpendiculaire à ce plan est nulle et ne "tire" pas sur le plan de l'orbite. Le fait que les nœuds soient quasi-stationnaires au moment des éclipses est très important, en effet les positions moyennes des nœuds sont alors presque égales aux positions vraies, donc dans l'étude des éclipses on peut utiliser le mouvement moyen des nœuds.
Le critère en latitude
On démontre qu'une éclipse de Lune se produira si, au moment de la pleine Lune (instant où la différence des longitudes géocentriques de la Lune et du Soleil est égale à 180°, c'est-à-dire au moment de l'opposition), la valeur absolue de la différence b des latitudes géocentriques apparentes du centre de la Lune et du centre du cône d'ombre est inférieure à 1,41° (1° 25' 23"), elle se produira peut-être si elle est comprise entre 1,41° (1° 25' 23") et 1,59° (1°35' 40") et elle ne se produira pas si elle est supérieure à 1,59° (1° 35' 40").
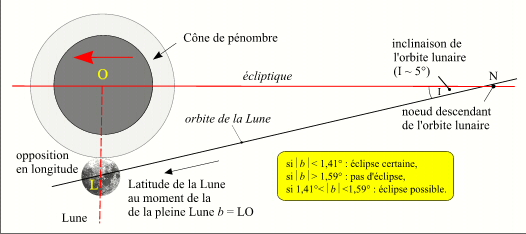
Critères en latitude pour les éclipses de Lune (vue depuis la Terre)
Crédit : IMCCE/Patrick Rocher
Sur la figure ci-dessus, la distance minimale correspond à l'instant où pour le centre de la Terre, le centre de la Lune est le plus près possible du centre du cône d'ombre, cela correspond si l'éclipse a lieu, au maximum de l'éclipse. Durant une éclipse de Lune on a toujours un des deux scénarios suivants :
- si l'éclipse a lieu avant le passage de la Lune au nœud, on observe d'abord l'opposition (pleine Lune), puis le maximum de l'éclipse, puis le passage au nœud,
- si l'éclipse a lieu après le passage de la Lune au nœud, on observe d'abord le passage au nœud, puis le maximum de l'éclipse et enfin l'opposition.
La géométrie de ce dessin montre également que plus l'opposition est proche du nœud, plus la distance minimale entre la Lune et le centre du cône d'ombre est petite et plus la grandeur (magnitude) de l'éclipse est grande. Ainsi, les éclipses par la pénombre correspondent à des oppositions situées loin des nœuds de l'orbite lunaire et les éclipses par l'ombre (partielles ou totales) correspondent à des oppositions proches des nœuds de l'orbite lunaire.
On peut détailler le critère en latitude en déterminant pour quelle valeur de b (0,89°) on a une éclipse par l'ombre avec certitude et pour quelle valeur de b (1,06°) on n'a pas d'éclipse par l'ombre avec certitude (mais une éclipse par la pénombre avec certitude); de même on peut déterminer pour quelle valeur de b (0,36°) on a une éclipse totale avec certitude et pour quelle valeur de b (0,53°) on n'a pas d'éclipse totale avec certitude, ces valeurs sont données dans le graphique ci-dessous.
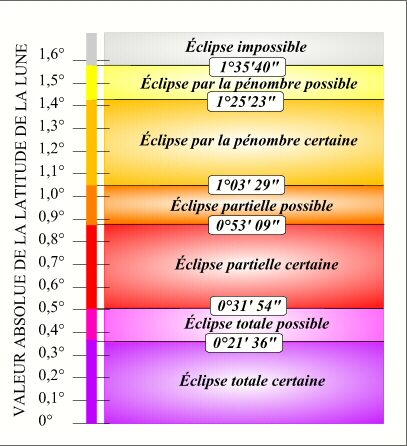
Crédit : IMCCE/Patrick Rocher
On peut également calculer les valeurs moyennes de ces critères en latitude. Pour avoir une éclipse de Lune par la pénombre il faut que b soit inférieure à βm = 1,49°, pour avoir une éclipse de Lune par l'ombre il faut que b soit inférieure à βm = 0,96° et pour avoir une éclipse totale de Lune il faut que b soit inférieure à βm = 0,44°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses par la pénombre (36%), la proportion d'éclipses par l'ombre (64%) et la proportion d'éclipses totales (30%).
 Remarque
Remarque
Les bornes d'existence des éclipses de Lune : 1,41° (1° 25' 23") et 1,59° (1°35' 40") sont très proches des limites des éclipses de Soleil : 1,41° (1° 24' 37") et 1,59° (1°34' 46"). Les écarts sont de l'ordre de la minute de degré. Les bornes des éclipses de Lune sont un peu plus grandes que les bornes des éclipses de Soleil en raison de la réfraction atmosphérique.
En savoir plus: La démonstration du critère en latitude
 En savoir plus
En savoir plus
La démonstration est en tout point identique à la démonstration du critère en latitude des éclipses de Soleil, il suffit de remplacer la conjonction par l'opposition et le Soleil par les cônes d'ombre et de pénombre de la Terre.
Nous allons établir le critère en latitude dans le cas d'une éclipse au nœud ascendant de l'orbite lunaire, l'opposition ayant lieu avant le passage au nœud. La démonstration est identique pour un passage au nœud descendant ou avec une opposition située après le passage au nœud, la seule chose qui change dans ce dernier cas est la position du minimum de distance entre des deux corps.
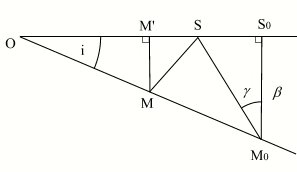
Critère en latitude
Crédit : IMCCE/Patrick Rocher
Soit M0 et S0 : les positions de la Lune et du centre du cône d'ombre à l'instant de l'opposition (pleine Lune) avant le passage de la Lune au nœud ascendant de son orbite.
M et S : les positions de la Lune et du centre du cône d'ombre à un instant t postérieur à l'opposition.
γ : l' angle S0M0S.
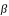 : la différence des latitudes entre la Lune et le centre du cône d'ombre à l'instant de l'opposition.
: la différence des latitudes entre la Lune et le centre du cône d'ombre à l'instant de l'opposition.
q : le rapport du mouvement en longitude de la Lune sur celui du centre du cône d'ombre (Soleil+180°).
Le calcul du critère en latitude consiste à calculer le minimum de la distance SM et de le comparer à la somme des demi-diamètres géocentriques apparents des cônes d'ombre 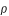 (et de pénombre
(et de pénombre 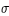 ) et du demi-diamètre de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore :
) et du demi-diamètre de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore :
On a :
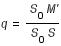 soit
soit 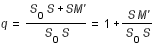
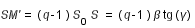 avec
avec 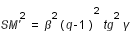
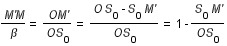
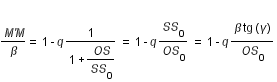
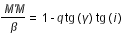
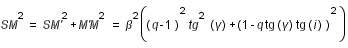 (1)
(1)
On introduit un angle auxiliaire i', tel que : 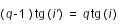
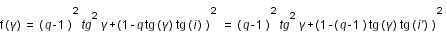
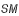 est minimum lorsque
est minimum lorsque 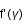 est nulle
est nulle
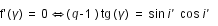 (2)
(2)
Ce qui correspond à : 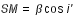 (3)
(3)
Cette distance correspond à une observation vue du centre de la Terre (coordonnées géocentriques).
En savoir plus: La démonstration du critère en latitude-2
 En savoir plus
En savoir plus
Il y a éclipse par la pénombre lorsque SM est inférieur à la somme des demi-diamètres apparents du cône de pénombre et de la Lune.
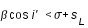
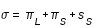
soit : 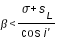 (4)
(4)
Il y a éclipse par l'ombre lorsque SM est inférieur à la somme des demi-diamètres apparents du cône d'ombre et de la Lune.
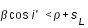
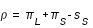
soit : 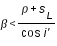 (5)
(5)
Il y a éclipse totale par l'ombre lorsque SM est inférieur à la différence des demi-diamètres apparents du cône d'ombre et de la Lune.
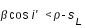
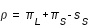
soit : 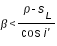 (6)
(6)
Il suffit alors de remplacer dans ces formules les paramètres par leurs valeurs extrêmes pour en déduire les critères en latitude.
Le tableau suivant donne les valeurs extrêmes des paramètres, l'étude des séries donnant l'orbite de la Lune, montre qu'au voisinage de la nouvelle Lune (et de la pleine Lune) la valeur de l'inclinaison est maximale, il convient donc de prendre i ~ 5° 17' dans ces formules.
|
maximum |
Minimum |
moyenne |
| q |
16,2 |
10,9 |
13,5 |
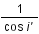
|
1,0052 |
1,0043 |
1,00472 |
Parallaxe Lune 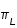
|
61' 27" |
53' 53" |
57' 2,70" |
Parallaxe Soleil 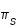
|
8,96" |
8,65" |
8,80" |
| 1/2 diamètre Lune sL
|
16' 45" |
14' 41" |
15' 32,58" |
| 1/2 diamètre Soleil sS
|
16' 18" |
15' 46" |
15' 59,63" |
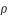 * * |
46' 27" |
38' 15" |
41' 45,73" |
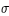 * * |
1° 18' 30" |
1° 10' 20" |
1° 13' 45" |
* Dans le calcul de ces valeurs on a tenu compte de la réfraction atmosphérique et de la parallaxe de la Lune à 45° de latitude en multipliant σ par (1+1/128) et ρ par (1+1/73).
Ainsi la valeur inférieure βMin du second membre de (4) est obtenue avec σ et sL minimales, la valeur supérieure βMax est obtenue avec σ et sL maximales et l'on obtient βMin=1°25'23" et βMax=1°35'40". Ce sont les limites d'existence des éclipses de Lune.
De même la valeur inférieure βMin du second membre de (5) est obtenue avec ρ et sL minimales, la valeur supérieure βMax est obtenue avec ρ et sL maximales et l'on obtient βMin=0°53'9,63" et ΔMax=1°3'28,6". Ce sont les limites d'existence des éclipses de Lune par l'ombre.
Et enfin la valeur inférieure βMin du second membre de (6) est obtenue avec ρ minimal et sL maximal, la valeur supérieure βMax est obtenue avec ρ maximal et sL minimal et l'on obtient βMin=0°21'35,52" et βMax=0°31'54,52". Ce sont les limites d'existence des éclipses totales de Lune.
Le critère en longitude
Le critère sur la latitude du centre de la Lune, peut se traduire en un critère sur la longitude de l'opposition Lune Soleil donc de la longitude du centre du cône d'ombre (Soleil +180°) par rapport au nœud de l'orbite lunaire. Ainsi il y aura éclipse si au moment de l'opposition en longitude, la différence de longitude entre le nœud de l'orbite lunaire et la longitude du centre du cône d'ombre est inférieure à 15,665°, il n'y aura pas d'éclipse si cette différence est supérieure à 17,375°, et il y aura peut-être éclipse si elle est comprise entre ces deux valeurs. Comme on le voit on a repris le même critère que dans le cas des éclipses de Soleil, en effet vu la faible différence des critères en latitude, on peut considérer que les critères en longitude sont identiques, en réalité les critères en longitude pour les éclipses de Lune sont un petit peu plus larges que les critères en longitude pour les éclipses de Soleil.
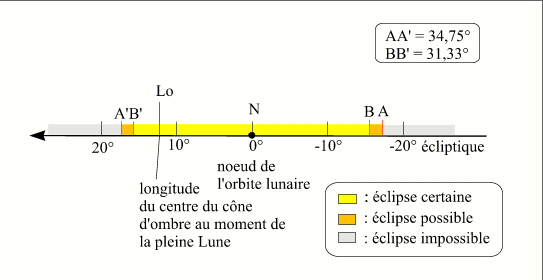
Critère en longitude pour les éclipses de Lune (vu depuis le centre de la Terre)
Crédit : IMCCE/Patrick Rocher
La figure suivante représente le critère en longitude vu dans le repère géocentrique écliptique.
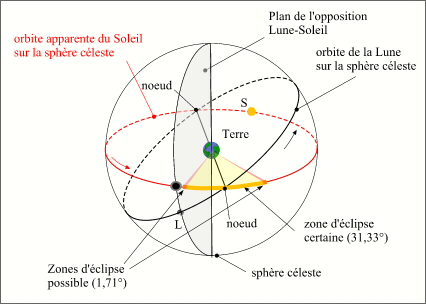
Critère en longitude pour les éclipses de Lune (vu depuis l'espace)
Crédit : IMCCE/Patrick Rocher
Nombre d'éclipses à chaque saison d'éclipse
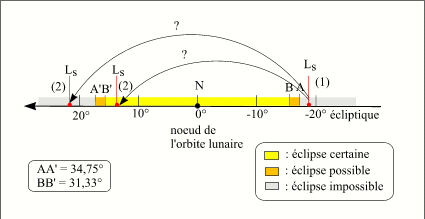
Critère en longitude pour les éclipses de Soleil (vu depuis le centre de la Terre)
Crédit : IMCCE/Patrick Rocher
En étudiant la figure ci-dessus, on peut se poser la question suivante. Supposons que nous ayons une conjonction en longitude (1) juste avant le point A, la conjonction suivante (2) va-t-elle être à l'intérieur ou à l'extérieur de l'arc BB' ? Pour répondre à cette question, on doit calculer de combien avance la longitude de la Terre (ou du soleil apparent) par rapport au nœud de l'orbite lunaire durant une révolution synodique de la Lune (une lunaison). On a vu que la Terre (ou le soleil apparent) passe par le même nœud de l'orbite lunaire tous les 346,62 jours, donc la vitesse de la Terre par rapport à la ligne des nœuds est de 360°/346,64jours = 1,0386°/jour, or la révolution synodique moyenne de la Lune est de 29,53 jours, donc entre deux conjonctions consécutives la longitude de la Terre varie de 1,0386 x 29,53 = 30,67°.
Or cette valeur est inférieure à la valeur de l'arc qui est égale à 31,33°. Donc à chaque passage de la Terre (ou du soleil apparent) par un nœud de l'orbite lunaire il y a obligatoirement une éclipse de Soleil au voisinage de la conjonction dont la longitude est la plus proche du nœud de l'orbite lunaire.
Au moins deux éclipses (Lune et Soleil)
On peut donner une information supplémentaire, comme le critère en longitude est le même pour les éclipses de Lune, une demi-lunaison avant ou après la conjonction (nouvelle Lune) la Lune est en opposition (pleine Lune) et la Terre n'a parcouru que 15,335° en longitude par rapport au nœud, ces 15,335° correspondent à l'écart angulaire entre une conjonction et une opposition. Donc si une conjonction se trouve dans l'arc BB' l'opposition suivante ou l'opposition précédente se trouve obligatoirement aussi sur cet arc et il y a une éclipse de Lune, mais à l'autre nœud de l'orbite lunaire.
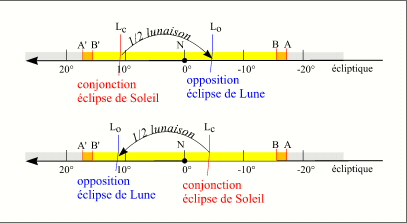
Conjonction et opposition au voisinage du nœud
Crédit : IMCCE/Patrick Rocher
À chaque saison d'éclipse, il y obligatoirement deux éclipses, une éclipse de Soleil et une éclipse de Lune.
Au plus trois éclipses (Lune et Soleil)
La variation de longitude de la Terre durant une lunaison étant de 30,67° et l'arc BB' ayant une longueur de 31,33°, il est également possible d'avoir deux conjonctions contenues dans l'arc BB'. Dans ce cas les conjonctions sont proches des extrémités de l'arc BB' et l'opposition comprise entre ces deux conjonctions est proche du nœud de l'orbite lunaire. De même on peut avoir deux oppositions dans l'arc BB'. Dans ce cas les oppositions sont proches des extrémités de l'arc BB' et la conjonction comprise entre ces deux oppositions se trouve proche du nœud de l'orbite lunaire. De plus comme nous l'avons déjà signalé, les éclipses proches des extrémités de l'arc BB' donc loin du nœud sont des éclipses faibles, donc des éclipses partielles de Soleil ou des éclipses de Lune par la pénombre et les éclipses proches du nœud sont des éclipses fortes, donc des éclipses centrales de Soleil ou des éclipses totales de Lune.
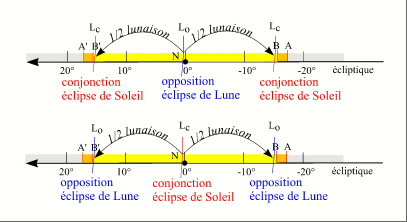
Conjonction et opposition au voisinage du nœud
Crédit : IMCCE/Patrick Rocher
On peut donc avoir une série de trois éclipses, au voisinage du passage de la Terre (ou du soleil apparent) par un nœud de l'orbite lunaire. Dans ce cas on a soit une éclipse forte de Soleil (éclipse centrale) encadrée par deux éclipses faibles de Lune (éclipses par la pénombre) ou une éclipse forte de Lune (éclipse totale) encadrée par deux éclipses faibles de Soleil (éclipses partielles).
Nombre d'éclipses par an
Une année civile du calendrier grégorien comporte 365 ou 366 jours. La lunaison moyenne est de 29,53 jours, une année lunaire de douze lunaisons a donc 354 jours, l'écart entre les deux années est de 11 ou 12 jours. Durant ces jours, la demi-lunaison étant supérieure à 14 jours, il ne peut pas y avoir à la fois une conjonction et une opposition. Donc une année civile ne peut jamais avoir à la fois 13 conjonctions (nouvelles Lunes) et 13 oppositions (pleines Lunes). Une seule de ces deux conjonctures est possible, dans ce cas la première conjonction ou opposition a lieu dans les 11 (ou 12) premiers jours de janvier et la dernière conjonction ou opposition a lieu dans les 11 (ou 12) derniers jours de décembre. On a donc, au maximum, soit une année civile à 13 oppositions, soit une année civile à 13 conjonctions. La saison des éclipses est égale à 173,31 jours, donc tous les 173 jours, aux conjonctions et oppositions les plus proches de ces dates il y a au moins deux éclipses (une de Soleil et une de Lune) et il y a au plus trois éclipses (deux de Lunes et une de Soleil ou deux de Soleil et une de Lune).
Une année civile peut contenir au maximum deux saisons d'éclipses entières, soit trois passages de la Terre par un des nœuds de l'orbite lunaire, le premier étant en début d'année, le second en milieu d'année et le dernier en fin d'année. À chacun de ces passages, on peut associer un couple ou un triplet d'éclipses. Mais l'on n'a jamais un triplet d'éclipses complet en début et en fin d'année, et dans le cas ou l'on a deux triplets complets à deux passages consécutifs le troisième passage ne comporte qu'une éclipse dans l'année en cours, car s'il présentait deux éclipses dans l'année en cours, il y aurait 13 oppositions et 13 conjonctions dans l'année, chose impossible. Donc dans une année civile, on a au maximum sept éclipses. Le tableau ci-dessous regroupe toutes les combinaisons possibles.
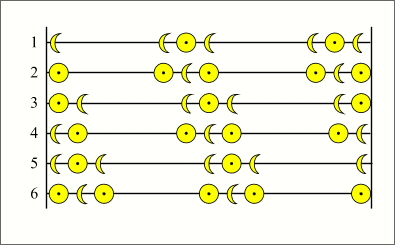
Liste des combinaisons possibles de 7 éclipses dans une année civile
Crédit : IMCCE/Patrick Rocher
On remarque dans ce tableau que les triplets d'éclipses qui se suivent à six lunaisons d'intervalle ont la même composition. En effet, comme on l'a déjà signalé, dans chaque triplet, l'éclipse médiane se produit très près du nœud, or l'éclipse médiane du triplet suivant sera forcement une éclipse du même corps, la conjonction ou l'opposition n'ayant avancé que de 4° environ. De plus lorsque l'on a sept éclipses par an la première et la dernière éclipses sont des éclipses du même corps, la première a toujours lieu dans les 11 (ou 12) premiers jours de janvier et la dernière a toujours lieu dans les 11 (ou 12) derniers jours de décembre.
En conclusion le nombre maximal d'éclipses dans une année civile est de sept éclipses, avec obligatoirement deux éclipses de Soleil et deux éclipses de Lune, pour les trois autres toutes les combinaisons sont possibles. Le nombre minimal d'éclipses dans une année est de quatre, avec obligatoirement deux éclipses de Lune et deux éclipses de Soleil.
Les séries courtes d'éclipses
Nous allons nous intéresser à l'évolution des éclipses au cours du temps. Supposons que nous ayons une éclipse de Lune à une date donnée comment sera l'éclipse suivante ?
Généralement les éclipses successives de Lune sont séparées par six lunaisons (liées à une saison d'éclipses), donc il y a alternance de nœud lunaire (nœud ascendant et nœud descendant). Nous avons vu que durant une lunaison la Terre (ou le Soleil apparent) progressait en moyenne de 30,67° en longitude par rapport à la ligne des nœuds de l'orbite lunaire, donc au bout de six lunaisons la Terre (ou le Soleil apparent) progresse de 6 x 30,67° = 184,02°, donc si dl1 est la différence de longitude entre l'opposition et le nœud de l'orbite lunaire pour la première éclipse, l'éclipse suivante a lieu au nœud suivant et la différence dl2 entre l'opposition et ce nœud est égale à dl1 - (184,02° - 180°) = dl1- 4,02°. Donc l'opposition se déplace par rapport aux nœuds successifs d'environ 4° dans le sens direct d'une éclipse à la suivante.
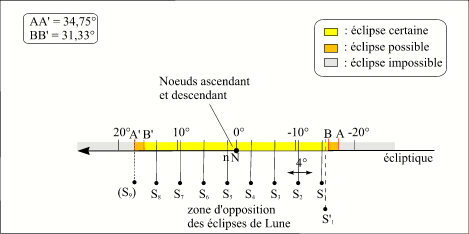
Série courte d'éclipse (vue depuis la Terre)
Crédit : IMCCE/Patrick Rocher
Les éclipses de la suite courte S1 à S8 ont lieu à chaque saison d'éclipse, alternativement au nœud ascendant puis au nœud descendant. Il y a toujours au moins 8 éclipses dans la suite car l'arc BB' contient 7 arcs de 4° donc 8 éclipses. Il peut éventuellement y avoir une neuvième éclipse S9 (dans l'arc A'B'), dans ce cas cette éclipse est la dernière éclipse d'un triplet d'éclipses : Lune-Soleil-Lune. Dans ce cas l'opposition correspondant à la première éclipse du triplet a lieu une lunaison plus tôt et se trouve 30,67° en amont et cette éclipse est la première éclipse de la série courte suivante; nous avons donc un décrochage dans la suite des séries, la série suivante commence avant que la série en cours ne soit terminée. Ce phénomène peut également se produire lorsque la huitième éclipse de la série est très proche du point B'. On peut donc conclure que les éclipses des suites courtes sont séparées par six lunaisons et que la première éclipse d'une suite courte est séparée de la dernière éclipse de suite courte précédente par cinq lunaisons ou par une lunaison (antérieure) dans le cas d'un décrochage.
On remarque que les oppositions liées aux éclipses d'une série courte parcourent l'arc BB' dans le sens direct avec un pas moyen de 4°, les premières et les dernières éclipses sont des éclipses faibles (éclipses par la pénombre) et les éclipses du milieu de la série, proches des nœuds, sont des éclipses fortes (éclipses partielles par l'ombre, puis éclipses totales).
Attention, il ne faut jamais oublier que ces calculs sont faits à l'aide des révolutions moyennes de la Lune, la réalité est toujours un peu différente, l'avance de l'opposition n'est jamais exactement égale à 4° mais varie autour de cette valeur moyenne.
Répartition des éclipses sur une période de 22 ans
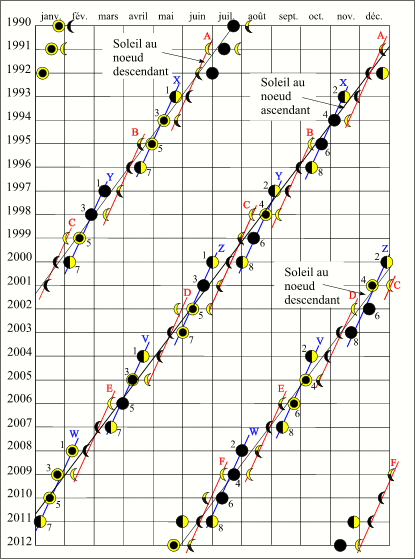
Éclipses de Lune et de Soleil entre 1990 et 2012.
Crédit : IMCCE/Patrick Rocher
Sur le diagramme ci-dessus nous avons fait figurer l'ensemble des éclipses de Lune et de Soleil comprises entre l'an 1990 et l'an 2012. Les éclipses sur ce diagramme sont représentées de la manière suivante :

Crédit : IMCCE/Patrick Rocher
On remarque que les éclipses ont bien lieu aux voisinages des passages du Soleil dans la direction des nœuds ascendant et descendant de l'orbite lunaire. Sur ce dessin nous avons signalé la nature des noeuds (ascendant ou descendant) relative au éclipses de Soleil. De même on constate qu'à chaque saison d'éclipse on a un doublet d'éclipses Lune-Soleil ou un triplet d'éclipses Lune-Soleil-Lune (1991) ou Soleil-Lune-Soleil (2000) et que dans le cas des triplets les éclipses en première et dernière positions sont faibles et que l'éclipse médiane est forte. On observe que les éclipses de Soleil ou de Lune de début et de fin de séries courtes sont séparées par cinq ou une lunaisons. On vérifie également qu'il y a toujours au moins quatre éclipses par an, sur la période de temps représentée, il n'y a pas d'année à 7 éclipses, mais une année à 6 éclipses (2000).
La démonstration de l'existence des séries courtes de Soleil est également valable pour des séries courtes d'éclipses de Lune. Il suffit de remplacer la conjonction par l'opposition. Sur notre diagramme nous avons fait figurer les séries courtes de Soleil (en bleu) et les séries courtes de Lune (en rouge). On constate que les traits joignant les éclipses d'une même série pour chaque nœud sont parallèles et coupent les lignes des nœuds. Sur la période considérée, il n'y a pas de série courte à 9 éclipses. Mais on peut observer plusieurs décrochage de séries courtes, par exemple la série courte de Soleil Z débute avant que la série Y soit terminée (triplet d'éclipses de l'an 2000).
Canons et grandeurs des éclipses de Lune
Introduction
 Introduction
Introduction
Dans cette section nous étudions la grandeur des éclipses de Lune. Qu'elles sont les éclipses les éclipses les plus longues et les éclipses les plus grandes en fonction des positions de la Lune par rapport au périgée et à l'apogée de son orbite et par rapport au position de la Terre sur son orbite.
Grandeurs des éclipses de Lune
Nous avons vu que la taille des cônes d'ombre et de pénombre dépend de deux paramètres, la distance Soleil-Terre qui conditionne la position des sommets des cônes et la distance Terre-Lune qui conditionne la position du plan d'intersection des cônes.
Les éclipses les plus longues seront des éclipses centrales, la durée de l'éclipse est fonction de la vitesse synodique de la Lune, c'est à dire de la différence des vitesses entre la Lune et les cônes d'ombre et de pénombre car la Lune et les cônes d'ombre et de pénombre se déplacent dans le même sens par rapport à la Terre (sens direct). Le tableau suivant donne les valeurs extrêmes du demi-diamètre apparent (ρ) du cône d'ombre en tenant compte des corrections de réfraction. Pour ces valeurs on donne également les positions de la Terre et de la Lune, la valeur du demi-diamètre apparent de la pénombre (σ), la vitesse synodique de la Lune en secondes de degré par heure, la grandeur de l'éclipse et la durée totale de l'éclipse.
Demi-diamètre de l'ombre 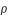
|
Minimal : 2,61sL
|
Moyen : 2,69 sL
|
Maximal 2,78 sL
|
| Positions de la Lune et de la Terre |
Lune apogée - Terre périhélie |
--- |
Lune périgée - Terre aphélie |
Demi-diamètre de la pénombre 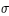
|
4253" = 4,82 sL
|
4425" = 4,75 sL
|
4678" = 4,65 sL
|
| Vitesse synodique de la Lune |
1626"/h |
1858"/h |
2150"/h |
| Grandeur de l'éclipse |
1,805 |
1,845 |
1,890 |
| Durée de l'éclipse |
environ 6h 19m |
environ 5h 46m |
environ 5h 17m |
La grandeur maximale s'observe dans le cas des éclipses centrales périgées (avec la Terre à l'aphélie), mais la durée maximale s'observe pour les éclipses apogées (avec la Terre au périhélie) ; en effet dans ce cas le diamètre apparent de la Lune est plus petit mais son mouvement synodique est plus lent. On retrouve donc la dualité déjà observée dans le cas des éclipses de Soleil de durée maximale (éclipses annulaires à l'apogée) et les éclipses de Soleil de grandeur maximale (éclipses totales au périgée).
Les canons d'éclipses de Lune
Les listes d'éclipses de Lune et de Soleil sont publiées dans des livres appelés canons d'éclipses. Le plus connu est celui de Theodor Ritter von Oppolzer, sa première édition date de 1887 dans le volume 52 des Mémoires de Mathématiques et de Sciences Naturelles de l'Académie Impériale de Vienne. Ce canon, corrigé, est réédité régulièrement par Dover Publications. Dans ce canon, on trouve 8000 éclipses de Soleil comprises entre -1207 et 2161 et 5200 éclipses de Lune comprises entre -1206 et 2132. Il faut préciser que l'on n'y trouve pas les éclipses de Lune par la pénombre.
Il convient de citer également le canon des éclipses de Lune de Jean Meeus et Hermann Mucke (1983, Astronomisches Büro, Vienne), contenant toutes les éclipses de Soleil comprises entre -2002 et +2526.
À l'IMCCE, nous avons construit un canon d'éclipses de Lune et de Soleil. Il porte sur une période de 6000 ans (de l'an -2999 à 3000), il a été construit avec les dernières théories planétaires et lunaire élaborées à l'IMCCE.
Ces trois canons ont été construits avec des théories différentes des corps célestes et avec des constantes légèrement différentes, cela implique que certaines éclipses limites ne sont pas identiques (apparition ou disparition d'éclipses limites par la pénombre, ou éclipses totales dans un canon qui deviennent partielles dans l'autre).
En savoir plus: Le canon de l'IMCCE
 En savoir plus: Le canon d'éclipses de Lune de l'IMCCE
En savoir plus: Le canon d'éclipses de Lune de l'IMCCE
Les théories utilisées
Pour construire notre canon nous avons utilisé les théories suivantes :
- Théorie de la Lune : ELP2000 de Michèle Chapront-Touzé et J. Chapront.
- Théorie du barycentre Terre-Lune : VSOP82 de P. Bretagnon.
- Éphémérides sous forme de polynômes de Tchebycheff : SLP98 de G. Francou
- TT-TU : valeurs de R. Stephenson (1984) modifiées et adaptées à la théorie de la Lune utilisée.
- Théorie de la précession de Lieske (1977).
- Théorie de la nutation de Wahr (1981).
- Temps sidéral d'Aoki (1992)
Les paramètres physiques
Les paramètres physiques utilisés sont les suivants :
- le demi-diamètre solaire = 15' 59.63".
- le rapport du rayon lunaire sur le rayon équatorial terrestre : k = 0,2725076.
- le rayon équatorial terrestre = 6378140m.
- On tient compte de la réfraction atmosphérique en augmentant le demi-diamètre géocentrique apparent de l'ombre de 1/73 et en augmentant le demi-diamètre géocentrique apparent de la pénombre de 1/128.
Les résultats
Nous avons trouvé sur cette période de 6000 ans, 14357 éclipses de Lune qui se répartissent de la manière suivante :
- Nombre d'éclipses totales : 4210 (soit 29,3% des éclipses).
- Nombre d'éclipses partielles : 5019. (soit 34,9% des éclipses)
- Nombre d'éclipses par la pénombre : 5128 ( soit 35,7%) dont 164 totales par la pénombre.
Comme on l'a prédit précédemment, on vérifie que la proportion d'éclipses par l'ombre est bien d'environ 64% et la proportion d'éclipses par la pénombre est bien d'environ 36%.
Les éclipses totales les plus longues
Comme nous venons de le voir, il n'y a pas coïncidence entre les éclipses totales les plus grandes et les éclipses totales les plus longues. Les éclipses les plus longues ont lieu avec une Lune proche de l'apogée.
Le tableau suivant donne les 21 éclipses du canon de l'IMCCE dont la durée de la phase totale est supérieure à 1h46m. On remarquera que la valeur maximale de la grandeur de ces éclipses est de 1.8176336.
| Date de l'éclipse |
Magnitude |
Durée de la phase totale |
| 29/06-2344-30/06/-2344 |
1.7559958 |
01h46m05s |
| 01/06-2203 |
1.7995766 |
01h46m37s |
| 04/05/-2062 |
1.7921950 |
01h46m36s |
| 06/04-1921 |
1.8050155 |
01h46m27s |
| 23/06/-1646 - 24/06/-1646 |
1.7914130 |
01h46m16s |
| 26/05/-1505 |
1.7992139 |
01h46m30s |
| 27/04/-1364 |
1.8054797 |
01h46m29s |
| 30/03/-1223 |
1.8010124 |
01h46m15s |
| 16/07/-503 |
1.7999741 |
01h46m04s |
| 11/04/-98 |
1.8002998 |
01h46m02s |
| 07/08/54 |
1.8104677 |
01h46m13s |
| 28/06/177 |
1.7716335 |
01h46m23s |
| 31/05/318 |
1.7820179 |
01h46m33s |
| 03/05/459 |
1.8176336 |
01h46m33s |
| 12/06/1443 |
1.8083912 |
01h46m15s |
| 24/05/1584 |
1.8152958 |
01h46m06s |
| 13/08/1859 |
1.8150878 |
01h46m28s |
| 16/07/2000 |
1.7686611 |
01h46m25s |
| 09/06/2123 |
1.7489899 |
01h46m07s |
| 19/06/2141 |
1.7416402 |
01h46m07s |
| 11/05/2264-12/05/2264 |
1.7985597 |
01h46m14s |
Parmi cette liste, chaque éclipse appartient à un triplet d'éclipses et est encadrée par deux éclipses partielles de Soleil. En effet l'opposition étant toujours proche du noeud donc du milieu de l'intervalle BB', la conjonction précédente et la conjonction suivante tombent également à l'intérieur de l'intervalle, on a donc toujours un triplet d'éclipses. Par exemple l'éclipse du 01/06/-2203 qui a la plus longue phase totale et qui a duré au total 6h 14m 10s, est encadrée par les éclipses partielles de Soleil du 18/05/-2203 et de 16/06/-2203.
Pour cette éclipse on peut vérifier que c'est bien une éclipse apogée avec une opposition proche du passage au nœud de l'orbite :
- le 01/06/-2203 à 19h 02m 46s UT : la Lune passe par le nœud descendant de son orbite.
- e 01/06/-2203 à 19h 09m 59s UT : maximum de l'éclipse de Lune.
- le 01/06/-2203 à 19h 10m 11s UT : Pleine Lune.
- le 03/06/-2203 à 01h 26m 53s UT : la Lune à l'apogée d=406185 km, diam. app. =29.5'.
On vérifie que conformément à ce que nous avons dit lors de la définition du critère en latitude, le maximum de l'éclipse a lieu entre l'instant du passage au nœud et l'instant de la pleine Lune lorsque le passage au nœud est antérieur à la pleine Lune.
Les éclipses totales les plus grandes
Les éclipses totales les plus grandes correspondent à des éclipses totales périgées. Le tableau ci-dessous nous donne les 26 éclipses totales de Lune du canon de l'IMCCE dont la grandeur est supérieure à 1,86.
| Date des éclipses |
Grandeur |
Durée de la phase totale |
| 08/07/-2977 |
1.8775476 |
01h39m15s |
| 29/07/-2420 |
1.8647245 |
01h40m04s |
| 15/01/-2326 |
1.8620205 |
01h38m35s |
| 27/03/-1874 |
1.8748617 |
01h40m19s |
| 16/02/-1751 |
1.8621251 |
01h39m52s |
| 04/06/-1552 |
1.8753223 |
01h40m19s |
| 07/05/-1411 |
1.8661648 |
01h40m22s |
| 09/04/-1270 |
1.8725565 |
01h40m16s |
| 12/09/-1241 - 13/09/-1241 |
1.8672238 |
01h38m32s |
| 28/02/-1147 - 01/03/-1147 |
1.8730227 |
01h39m45s |
| 24/07/-1136 |
1.8776169 |
01h39m10s |
| 29/12/-540 |
1.8636202 |
01h38m10s |
| 09/01/-521 -10/01/-521 |
1.8684891 |
01h38m15s |
| 01/04/-51 |
1.8634609 |
01h39m44s |
| 10/02//54 - 11/02/54 |
1.8693552 |
01h39m16s |
| 17/07/83 |
1.8618347 |
01h41m49s |
| 06/09/564 |
1.8743438 |
01h38m54s |
| 30/07/687 |
1.8620946 |
01h39m18s |
| 24/04/1092 |
1.8737558 |
01h39m20s |
| 28/09/1121 |
1.8682270 |
01h38m55s |
| 09/08/1226 |
1.8794485 |
01h39m39s |
| 15/05/1631 |
1.8728523 |
01h39m48s |
| 30/08/1765 |
1.8631087 |
01h41m28s |
| 26/07/1953 |
1.8628642 |
01h40m44s |
| 04/11/2264 - 05/11/2264 |
1.8688193 |
01h38m37s |
| 05/06/2756 |
1.8799400 |
01h39m20s |
Chaque éclipse de Lune de cette liste appartient à un triplet d'éclipses et est encadrée par deux éclipses partielles de Soleil. Par exemple, l'éclipse du 05/06/2756 qui est la plus grande, dont la durée totale est de 5h 17m 31s, est encadrée par les éclipses partielles de Soleil du 21/05/2756 et du 19/06/2756.
Pour cette éclipse on peut vérifier que c'est bien une éclipse périgée avec une opposition proche du passage au nœud de l'orbite :
- le 05/06/2756 à 03h 38m 22s UT : la Lune passe par le nœud ascendant de son orbite.
- le 05/06/2756 à 03h 41m 34s UT : maximum de l'éclipse de Lune.
- le 05/06/2756 à 03h 41m 40s UT : Pleine Lune.
- le 05/06/2756 à 09h 01m 51s UT : la Lune au périgée d=357129 km, diam. app. =33.5'.
On vérifie de nouveau que le maximum de l'éclipse a lieu entre le passage au nœud et la pleine Lune.
Les éclipses les plus faibles et les plus courtes
Contrairement au cas des éclipses totales de Lune de grandeur maximale et des éclipses totales de Lune de durée maximale, il y a coïncidence entre les éclipses de Lune les plus courtes et les éclipses de grandeur minimale. Il s'agit d'éclipses rasantes par l'ombre dans le cas des éclipses partielles et par la pénombre dans le cas des éclipses par la pénombre. Le tableau ci-dessous nous donne les 6 éclipses partielles de Lune du canon de l'IMCCE dont la grandeur est inférieure à 0,001.
| Date de l'éclipse |
Grandeur |
Durée de la phase partielle |
| 14/09/-2237 |
0.0009512 |
7m36s |
| 08/08/-1463 |
0.0002822 |
3m39s |
| 02/07/-754 |
0.0004297 |
4m47s |
| 13/10/273 |
0.0000806 |
1m58s |
| 24/022157 |
0.0004892 |
5m27s |
| 16/06/2421 |
0.0006280 |
5m34s |
Le tableau ci-dessous nous donne les 2 éclipses de Lune par la pénombre du canon de l'IMCCE dont la grandeur est inférieure à 0,001.
| Date de l'éclipse |
Grandeur |
Durée de l'éclipse |
| 07/07/1571 |
0.0004848 |
5m53s |
| 17/01/2986 |
0.0006936 |
8m01s |
Ces deux dernières éclipses de Lune appartiennent à des triplets d'éclipses. Ainsi l'éclipse du 07/07/1571 est la première du triplet comprenant ensuite l'éclipse annulaire de Soleil des 21 et 22/07/1571 puis l'éclipse partielle de Lune du 05/08/1571. De même l'éclipse du 17/01/2986 est la première du triplet comprenant ensuite l'éclipse annulaire-totale de Soleil du 31/01/2986 puis l'éclipse de Lune par la pénombre du 15/02/2986.
Il convient de remarquer que ces éclipses sont des cas limites propres au canon de l'IMCCE, les cas limites des autres canons d'éclipses de Lune sont différents, les constantes et les éphémérides utilisées pour l'élaboration des canons étant différentes.
Le Saros et les suites longues d'éclipses de Lune
Introduction
 Introduction
Introduction
Dans cette section, nous reprenons la notion de Saros et du nombre moyen d'éclipses de Lune dans un Saros. Nous étudions l'évolution des éclipses dans les séries longues d'éclipses homogènes et nous donnons un exemple de série longue d'éclipses.
Nombre d'éclipses dans un Saros
Le définition du saros et les démonstrations qui lui sont liées ont été traitées dans la partie relative aux éclipses de Soleil. Nous redonnons ici que les particularités propres aux nombres d'éclipses.
Le saros comporte 38 saisons d'éclipses, revenant en moyenne toutes les 5 ou 6 lunaisons. À chaque saison d'éclipses il y a au moins deux éclipses et parfois trois éclipses. En moyenne un saros comprend 84 éclipses, réparties en 42 éclipses de Soleil et 42 éclipses de Lune.
Les 42 éclipses de Lune se répartissent de la manière suivante : 14 éclipses par la pénombre, 28 éclipses par l'ombre dont 14 éclipses partielles et 14 éclipses totales.
Les 42 éclipses de Soleil se répartissent de la manière suivante : 14 éclipses partielles et 28 éclipses centrales.
Ce nombre d'éclipses par saros est une valeur moyenne, en réalité il existe des saros riches pouvant atteindre jusqu'à 94 éclipses (47 de chaque) et des saros pauvres comportant 78 éclipses.
Les canons d'éclipses construits à l'IMCCE comportent 28512 éclipses sur une période de 5999 ans, soit en moyenne 4,7528 éclipses par an et 85,7 éclipses par saros (valeur que l'on peut arrondir à 86). Cette valeur est légèrement plus forte que la valeur moyenne (84). On retrouve le saros moyen du canon d'Oppolzer, construit sur une période plus courte, qui est de 86 éclipses.
Eclipses homologues et suites longues d'éclipses de Lune
Nous avons vu qu'il existe une période de récurrence des éclipses, le saros, qui ramène sensiblement la même éclipse après une période de 6585,32 jours. Ces éclipses séparées par un saros sont appelées éclipses homologues. En réalité, elles ne sont pas parfaitement identiques, mais elles évoluent légèrement d'un saros à l'autre et elles forment des suites qui portent sur de grandes périodes de temps d'où leur nom de suites longues.
Evolution de la longitude de l'opposition après un saros
Nous allons regarder comment évolue la longitude de l'opposition après une période d'un saros. L'écart entre le saros de 223 lunaisons « L » et les 242 révolutions draconitiques « G » est de moins 52 minutes de temps (- 0,03612 jour).
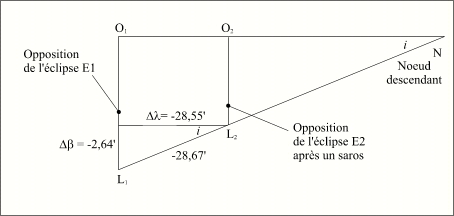
Variation de la longitude de l'opposition entre deux éclipses homogènes
Crédit : IMCCE/Patrick Rocher
Durant ces 52 minutes la Lune, sur son orbite, se déplace en moyenne par rapport à son nœud de -0,03612 x 360°/G = -28,67'. La Lune en opposition se trouve donc déplacée sur son orbite de 28,67' dans le sens rétrograde par rapport au nœud. Compte tenu de l'inclinaison de l'orbite lunaire, ce décalage se traduit par un décalage de la longitude céleste Δλ = -28,55' et par une variation de la latitude céleste de la Lune de Δβ = -2,64'.
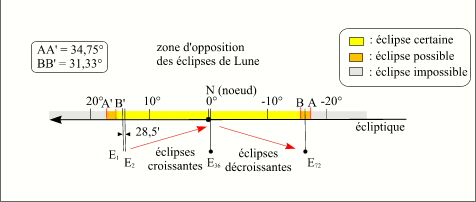
Évolution sur une suite longue d'éclipses
Crédit : IMCCE/Patrick Rocher
Les oppositions des éclipses homologues vont donc parcourir l'arc BB' dans le sens rétrograde avec un pas moyen de 28,55'. Si l'on divise l'arc BB' par 28,55', on constate qu'il peut contenir 66 éclipses et si l'on divise l'arc AA' par 28,55' on voit qu'il peut contenir 74 éclipses. Ces suites d'éclipses sont appelées suites longues. L'étude des canons d'éclipses montre qu'en moyenne ces suites comportent 72 éclipses. Ce qui correspond à une période de temps d'environ 1300 ans.
Aspect d'une suite longue d'éclipse de Lune
Les premières éclipses d'une suite longue sont faibles, car elles sont proches de l'arc A'B', donc loin du nœud. Ensuite, leur grandeur va croître jusqu'à ce qu'elles se produisent au voisinage du nœud, puis leur grandeur va décroître pour finir de nouveau faible au voisinage de l'arc BA. Pour une suite longue de 72 éclipses, si l'on respecte les pourcentages des différents types d'éclipses (environ 1/3 de chaque), on aura donc successivement 12 éclipses par la pénombre de grandeur croissante, puis 12 éclipses partielles par l'ombre, puis 12 éclipses totales de grandeur croissante (sur 650 ans), puis de nouveau 12 éclipses totales de grandeur décroissante, puis 12 éclipses partielles par l'ombre et enfin 12 éclipses par la pénombre de grandeur décroissante (sur 650 ans). Dans la pratique, les deux ou trois éclipses du milieu de la suite longue sont maximales, elles servent de transition entre la période de croissance et de décroissance des éclipses totales. On remarque que toutes les éclipses d'une suite ont lieu au même nœud. Si la suite longue a lieu au nœud descendant les latitudes célestes successives de la Lune croissent des latitudes négatives aux latitudes positives, les positions de la Lune par rapport aux cônes d'ombre et de pénombre de la Terre vont donc se déplacer du sud au nord. Inversement pour une suite longue au nœud ascendant les latitudes célestes successives de la Lune décroissent des latitudes positives aux latitudes négatives, les positions de la Lune par rapport aux cônes d'ombre et de pénombre de la Terre vont donc se déplacer du nord au sud. En réalité, dans les propos précédents, les directions nord et sud désignent le nord et le sud par rapport à l'écliptique et non par rapport à l'équateur terrestre, il faut bien se rappeler que l'écliptique est incliné par rapport à l'équateur terrestre.
Evolutions des éclipses homologues
Evolution en longitude terrestre
Nous avons vu que la période du saros n'est pas un nombre entier de jours, sa valeur est de 6585,32 jours. Donc entre deux éclipses homologues, la Terre n'a pas tourné d'un nombre entier de jour, les zones concernées par les éclipses ne sont donc pas les mêmes. En 0,32 jour, la Terre tourne d'environ 120°, les zones concernées par l'éclipse se déplacent donc d'environ 120° vers l'ouest. Comme une éclipse de Lune est visible, au moins durant une partie de sa durée, sur environ les deux tiers de la surface terrestre, il n'est pas surprenant que des éclipses homologues successives soient visibles d'un même lieu. Après trois saros, l'éclipse a même lieu sensiblement au même instant. Cela explique que la période de récurrence des éclipses (saros) soit plus facilement décelable, en un lieu, à travers les suites d'éclipses de Lune observées. Ce qui n'est pas le cas pour les éclipses de Soleil.
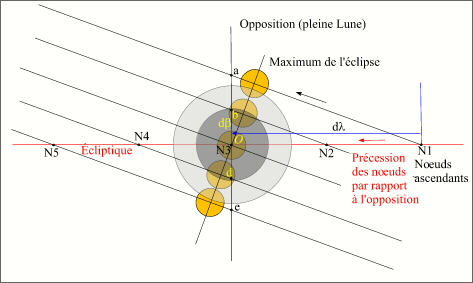
Évolution en latitude
Crédit : IMCCE/Patrick Rocher
Evolution en latitude écliptique par rapport aux cônes d'ombre et de pénombre
Le dessin ci-dessus nous montre l'évolution des éclipses homogènes de Lune durant une suite longue de saros au nœud ascendant. Sur cette figure nous avons figée la longitude de la pleine Lune (opposition), ce sont donc les positions du nœud ascendant qui vont variées dans le sens direct par rapport à l'opposition au cours du temps. Nous avons représenté la position du nœud ascendant environ tous les 325 ans ainsi que les maxima des éclipses correspondantes c'est-à-dire les distances minimales entre le centre de la Lune et le centre des cônes.
Au début de la suite longue d'éclipse de Lune, le nœud se trouve en position N1, à l'ouest de l'opposition, la Lune va donc passer d'ouest en est devant le bord nord du cône de pénombre, les premières éclipses de la suite seront donc des éclipses par la pénombre passant au bord nord de la pénombre (éclipsant donc le sud de la Lune). 325 ans plus tard, le nœud ascendant de l'orbite lunaire est en N2, la Lune rencontre le bord nord du cône d'ombre, les éclipses de Lune sont donc partielles par l'ombre. 325 ans plus tard, le nœud ascendant N3 est confondu avec la longitude de l'opposition, c'est le cas idéal d'une éclipse totale centrale, puis nous avons une situation symétrique par rapport à l'opposition, c'est-à-dire un nœud en N4 correspondant à des éclipses partielles par l'ombre mais au sud du cône d'ombre (éclipsant le nord de la Lune), puis des éclipses par la pénombre au sud du cône de pénombre qui prennent fin après la dernière position N5 du nœud.
On remarque que lorsque le nœud ascendant est à l'ouest de l'opposition le maximum de l'éclipse a lieu avant l'opposition, et que lorsque le nœud ascendant est à l'est de l'opposition le maximum de l'éclipse a lieu après l'opposition. Donc la connaissance de l'instant du maximum de l'éclipse, de l'instant de l'opposition et de la nature du nœud (ascendant ou descendant) permet de situer la position de l'éclipse dans la suite longue d'éclipses homogènes et la partie de la Lune éclipsée. Ou bien, inversement , la connaissance de la position d'une éclipse dans sa suite longue et la nature du nœud permet de savoir si le maximum de l'éclipse a lieu avant ou après l'opposition et de connaître la partie de la Lune éclipsée.
En savoir plus: Positions des éclipses d'une saison éclipse
 En savoir plus
En savoir plus
Positions des éclipses d'une saison dans les suites longues de saros
Nous avons vu qu'à chaque saison d'éclipse il y a soit un doublet soit un triplet d'éclipses de Lune et de Soleil. Nous allons essayer de déterminer les positions des éclipses de Lune et de Soleil dans leurs suites longues respectives en fonction de l'allure du triplet ou du doublet d'éclipses. On rappelle que lors d'une saison d'éclipse il y a inversion des nœuds avec la nature des éclipses, ainsi si l'éclipse ou les éclipses de Soleil ont lieu au nœud ascendant l'éclipse ou les éclipses de Lune de la même saison ont lieu au nœud descendant et inversement.
Cas d'un doublet d'éclipses
Dans le cas d'un doublet d'éclipses, l'opposition et la conjonction (les syzygies) sont toujours réparties de part et d'autre des nœuds. Donc l'éclipse correspondant à la syzygie à l'ouest (à droite) du nœud est dans la partie décroissante de sa suite longue et l'éclipse correspondant à la syzygie à l'est (à gauche) du nœud suivant est dans la partie croissante de sa suite longue.
 Exemple
Exemple
Soit un doublet constitué d'une éclipse de Lune au nœud descendant suivie d'une éclipse de Soleil au nœud ascendant. Comme l'éclipse de Lune a lieu avant le passage au nœud, l'opposition est à l'ouest du nœud et l'éclipse de Lune est dans la partie décroissante de sa suite longue (au nœud descendant) et c'est donc la partie sud du disque lunaire qui est éclipsée. L'éclipse de Soleil, elle, a lieu après le passage au nœud, la conjonction est donc à l'est du nœud et l'éclipse de Soleil est dans la partie croissante de sa suite longue (au nœud ascendant), elle sera donc visible dans l'hémisphère nord.
Le tableau ci-dessous résume tous les cas possibles pour un doublet d'éclipses
| Ordre du doublet |
Eclipse de Lune - Eclipse de Soleil |
Eclipse de Soleil - Eclipse de Lune |
| Position de l'éclipse de Lune dans sa suite longue |
partie déroissante |
partie croissante |
| Position de l'éclipse de Soleil dans sa suite longue |
partie croissante |
partie décroissante |
| Eclipse Lune au noeud descendant
Eclipse de Soleil au noeud ascendant |
partie sud du disque lunaire éclipsée
éclipse solaire visible au nord |
partie nord du disque lunaire éclipsée
éclipse solaire visible au sud |
| Eclipse Lune au noeud ascendant
Eclipse Soleil au noeud descendant |
partie nord du disque lunaire éclipsée
éclipse solaire visible au sud |
partie sud du disque lunaire éclipsée
éclipse solaire visible au nord |
Cas d'un triplet d'éclipses
Dans le cas d'un triplet d'éclipses, la première et la troisième éclipses sont de même nature (éclipses de Lune ou éclipses de Soleil) et la seconde éclipse est de nature opposée aux deux autres. La première éclipse appartient à la partie décroissante de sa suite longue et est proche de la fin de cette suite. La troisième appartient à la partie croissante de sa suite longue et est proche du début de cette suite. Pour l'éclipse du milieu, elle est proche du maximum dans sa suite longue, on peut la situer dans la partie croissante ou décroissante de sa suite, uniquement si l'on connaît la position de la syzygie par rapport au nœud, une syzygie à l'ouest du nœud la place dans la partie décroissante et une syzygie à l'est du nœud la place dans la partie croissante de sa suite.
 Remarque
Remarque
Dans les explications ci-dessus, la position à l'ouest (à droite) du nœud est équivalente à une syzygie antérieure au passage au nœud et une position à l'est (à gauche) est équivalente à une syzygie postérieure au passage au nœud. De même nous avons basé nos explications sur les positions relatives des nœuds et des syzygies, nous aurions pu faire les mêmes raisonnements en remplaçant un des deux éléments par la position, ou l'instant, du maximum des éclipses.
Evolutions des suites homologues - suite
Variation sur le fond d'étoile et dans l'année
Nous rappelons que d'un saros à l'autre, le Soleil, donc l'éclipse se décale d'environ 10,5° par rapport aux constellations zodiacales. Au cours d'une suite longue le soleil apparent effectue plus de deux tours complets d'orbite et l'on rencontre toutes les configurations liées au soleil apparent. Les éclipses parcourent les quatre saisons et cela deux fois.
Variation des types d'éclipses
Nous avons vu également que suite à l'écart entre un saros et 239 révolutions anomalistiques, la distance de la Lune à son périgée varie de 2,8° d'un saros à l'autre. Au cours d'une suite longue de 72 saros, les conjonctions lunaires liées aux éclipses homologues (donc la Lune) ne vont parcourir que 202° de l'orbite lunaire, soit un peu plus que la moitié. De plus durant les 48 éclipses centrales du saros, cet arc se réduit à 134°, il convient de comparer cette valeur avec les portions de l'orbite lunaire où les éclipses sont totales ou annulaires.
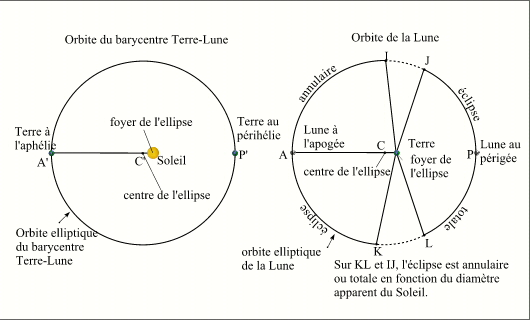
Orbites de la Terre et de la Lune
Crédit : IMCCE/Patrick Rocher
Ainsi si le périgée est proche du milieu de cet arc de 134°, la suite longue est riche en éclipses totales, si au contraire, cet arc avoisine l'apogée la suite longue est riche en éclipses annulaires.
 Remarque
Remarque
Il ne faut jamais perdre de vu que toutes les variations dans les suites longues sont calculées avec des valeurs moyennes et ne sont jamais tout à fait conformes à la réalité. Ainsi le décalage de la conjonction par rapport au nœud de 28,55' est une valeur moyenne. En réalité le Soleil avance plus vite en janvier (il est proche du périgée) qu'en juillet (proche de l'apogée), le calcul montre que la variation de la longitude de la conjonction par rapport au nœud est de l'ordre de 6' en janvier (au lieu de 28,55') et qu'elle atteint 48' en juillet. Les éclipses homologues d'hiver sont donc plus semblables que les éclipses homologues d'été qui évoluent sensiblement plus vite.
Il est facile de connaître la position d'une éclipse dans une suite longue d'éclipses. Les éclipses croissantes ont toujours lieu après le passage au nœud et les éclipses décroissantes ont toujours lieu avant le passage au nœud. La connaissance des instants des syzygies et du passage au nœud permet donc de positionner l'éclipse dans sa suite longue. Inversement la connaissance de la position d'une éclipse dans sa suite longue permet, sauf pour l'éclipse maximale, de savoir sa position par rapport aux nœuds. De plus dans le cas d'un doublet d'éclipses (Lune Soleil ou Soleil Lune) la première éclipse, qui a lieu avant le passage au nœud appartient à la partie décroissante de sa suite longue et la seconde éclipse appartient à la partie croissante de sa suite longue. Dans le cas d'un triplet d'éclipses, la première appartient à la fin de la partie décroissante de la suite longue qui la contient, la dernière appartient au début de la partie croissante de la suite longue qui la contient et l'éclipse médiane se trouve au voisinage du maximum de sa suite longue.
En savoir plus: Exemple de Saros
 En savoir plus
En savoir plus
Exemple de suite longue
Le tableau suivant donne la liste des éclipses de la suite longue contenant l'éclipse du 31 mai 2003. On donne successivement le numéro de l'éclipse dans la suite longue, le type d'éclipse, la date de l'éclipse, sa magnitude et la durée maximale de la phase centrale lorsque cette phase existe.
| N° |
type |
date |
magnitude |
durée |
| 1 |
P |
12/10/1624 |
0.0085968 |
|
| 2 |
P |
23/10/1642 |
0.0548679 |
|
| 3 |
P |
03/11/1660 |
0.0896182 |
|
| 4 |
P |
14/11/1678 |
0.1146153 |
|
| 5 |
P |
24/11/1696 |
0.1316624 |
|
| 6 |
P |
07/12/1714 |
0.1419092 |
|
| 7 |
P |
17/12/1732 |
0.1469513 |
|
| 8 |
P |
28/12/1750 |
0.1505860 |
|
| 9 |
P |
08/01/1769 |
0.1530883 |
|
| 10 |
P |
19/01/1787 |
0.1591577 |
|
| 11 |
P |
30/01/1805 |
0.1675941 |
|
| 12 |
P |
11/02/1823 |
0.1857746 |
|
| 13 |
P |
21/02/1841 |
0.2097100 |
|
| 14 |
P |
04/03/1859 |
0.2462690 |
|
| 15 |
P |
15/03/1877 |
0.2919636 |
|
| 16 |
P |
26/03/1895 |
0.3533467 |
|
| 17 |
P |
06/04/1913 |
0.4246662 |
|
| 18 |
P |
17/04/1931 - 18/04/1931 |
0.5110283 |
|
| 19 |
P |
28/04/1949 |
0.6095708 |
|
| 20 |
P |
09/05/1967 |
0.7205292 |
|
| 21 |
P |
19/05/1985 |
0.8411277 |
|
| 22 |
A |
31/05/2003 |
0.9696001 |
03m34.08s |
| 23 |
A |
10/06/2021 |
0.9721316 |
03m47.99s |
| 24 |
A |
21/06/2039 |
0.9730915 |
04m01.45s |
| 25 |
A |
01/07/2057 - 02/07/2057 |
0.9735738 |
04m18.67s |
| 26 |
A |
13/07/2075 |
0.9737206 |
04m40.41s |
| 27 |
A |
23/07/2093 |
0.9737206 |
05m06.77s |
| 28 |
A |
04/08/2111 |
0.9731384 |
05m36.78s |
| 29 |
A |
14/08/2129 - 15/08/2129 |
0.9724857 |
06m09.32s |
| 30 |
A |
26/08/2147 |
0.9716470 |
06m42.98s |
| 31 |
A |
05/09/2165 |
0.9706588 |
07m15.78s |
| 32 |
A |
16/09/2183 - 17/09/2183 |
0.9695596 |
07m46.87s |
| 33 |
A |
28/09/2201 |
0.9684309 |
08m14.61s |
| 34 |
A |
09/10/2219 |
0.9672517 |
08m39.72s |
| 35 |
A |
19/10/2237 |
0.9661547 |
09m00.30s |
| 36 |
A |
30/10/2255 - 31/10/2255 |
0.9651065 |
09m17.21s |
| 37 |
A |
10/11/2273 |
0.9642541 |
09m28.20s |
| 38 |
A |
21/11/2291 |
0.9635287 |
09m34.68s |
| 39 |
A |
02/12/2309 - 03/12/2309 |
0.9630803 |
09m34.31s |
| 40 |
A |
14/12/2327 |
0.9628599 |
09m28.43s |
| 41 |
A |
24/12/2345 |
0.9629606 |
09m15.58s |
| 42 |
A |
04/01/2364 - 05/01/2364 |
0.9633421 |
08m57.77s |
| 43 |
A |
15/01/2382 |
09640683 |
08m34.41s |
| 44 |
A |
26/01/2400 |
0.9651082 |
08m07.46s |
| 45 |
A |
05/02/2418 - 06/02/2418 |
0.9664621 |
07m37.67s |
| 46 |
A |
17/02/2436 |
0.9681073 |
07m06.45s |
| 47 |
A |
27/02/2454 |
0.9700297 |
06m34.42s |
| 48 |
A |
09/03/2472 - 10/03/2472 |
0.9721718 |
06m02.57s |
| 49 |
A |
21/03/2490 |
0.9745093 |
05m31.07s |
| 50 |
A |
01/04/2508 |
0.9769654 |
05m00.43s |
| 51 |
A |
12/04/2526 - 13/04/2526 |
0.9795505 |
04m29.66s |
| 52 |
A |
23/04/2544 |
0.9821258 |
03m59.66s |
| 53 |
A |
04/05/2562 |
0.9847154 |
03m29.01s |
| 54 |
A |
14/05/2580 -15/05/2580 |
0.9871679 |
02m58.81s |
| 55 |
A |
26/05/2598 |
0.9895234 |
02m27.78s |
| 56 |
A |
06/06/2616 |
0.9916211 |
01m58.16s |
| 57 |
A |
17/06/2634 |
0.9935042 |
01m29.84s |
| 58 |
A |
27/06/2652 - 28/06/2652 |
0.9950354 |
01m05.79s |
| 59 |
A |
09/07/2670 |
0.9961687 |
00m47.26s |
| 60 |
A |
19/07/2688 |
0.9967399 |
00m36.25s |
| 61 |
A |
31/07/2706 -01/08/2706 |
0.9960352 |
00m.36.88s |
| 62 |
P |
11/08/2724 |
0.8822576 |
|
| 63 |
P |
22/08/2742 |
0.7560645 |
|
| 64 |
P |
01/09/2760 |
0.6399250 |
|
| 65 |
P |
13/09/2778 |
0.5318151 |
|
| 66 |
P |
23/09/2796 |
0.4338706 |
|
| 67 |
P |
04/102814 |
0.3469499 |
|
| 68 |
P |
15/10/2832 |
0.2725393 |
|
| 69 |
P |
26/10/2850 |
0.2098505 |
|
| 70 |
P |
05/11/2868 |
0.1587829 |
|
| 71 |
P |
17/11/2886 |
0.1194801 |
|
| 72 |
P |
28/11/2904 |
0.0907818 |
|
| 73 |
P |
09/12/2922 |
0.0696946 |
|
| 74 |
P |
20/12/2940 |
0.0570489 |
|
| 75 |
P |
31/12/2958 |
0.0487713 |
|
| 76 |
P |
10/01/2977 |
0.0452276 |
|
| 77 |
P |
22/01/2995 |
0.0403169 |
|
On remarque que cette suite n'est pas complète, en effet le canon d'éclipse de l'IMCCE s'arrête en 2999, il y a probablement des éclipses de la suite qui sont postérieures à cette date. Malgré cela on dépasse la valeur moyenne de 72 éclipses. Et l'on est assez loin des valeurs moyennes, ainsi le nombre d'éclipses partielles de la partie croissante est de 21, la moyenne donne 12 ! On constate également que toutes les éclipses centrales sont des éclipses annulaires, donc l'arc parcouru par les conjonctions lunaires est au voisinage de l'apogée. L'éclipse du 31 mai 2003 est la première éclipse centrale de la partie croissante de la suite, on peut donc en déduire qu'elle a lieu après le passage au nœud et relativement longtemps après ce passage. De plus elle est proche d'un des pôles terrestre. On ne peut pas savoir si la suite est au nœud ascendant ou descendant de l'orbite lunaire. Pour cela il suffit de connaître la latitude de la Lune à la conjonction pour une seule éclipse de la suite. Cette longitude est positive pour l'éclipse du 31 mai donc cette suite longue est au nœud ascendant et l'éclipse du 31 mai 2003 est proche du pôle nord terrestre et les éclipses de la suite vont parcourir le globe terrestre du nord au sud.
Les éphémérides de la Lune nous donnent les informations suivantes :
- le 28/05/2003 à 13h 04m 44s UT : la Lune à l'apogée (distance maximale à la Terre) d=406168 km, diam. app. =29.5'.
- le 30/05/2003 à 08h 32m 17s UT : la Lune passe par le nœud ascendant de son orbite, long. moyenne = +59° 30,9'.
- le 31/05/2003 à 04h 08m 18s UT : maximum de l'éclipse annulaire de Soleil.
- le 31/05/2003 à 04h 19m 51s UT : Nouvelle Lune.
On constate que le maximum de l'éclipse a bien lieu entre le passage et la conjonction, qu'il est proche de la conjonction (11m 33s) mais éloigné du passage au nœud (19h 36m 1s). L'éclipse est proche du passage de la Lune à l'apogée elle est donc annulaire.
Les éclipses anciennes
Introduction
 Introduction
Introduction
Dans cette section nous étudions quelques éclipses anciennes de Lune ainsi que leur prédiction et observation.
Visibilité des éclipses anciennes à l'oeil nu
L'Astronomie des Césars fut publiée par Petrus Apianus en 1540. Dédiée à Charles Quint et à son frère Ferdinand, l'Astronomie des Césars permet de déterminer les positions planétaires, ainsi que les éclipses, pour une période comprise entre 7000 av. J.-C. et 7000 apr. J.-C. ! Apianus utilise à la perfection l'usage des disques mobiles, ou " volvelles ". Des fils de soie permettent de lire les graduations sur les cadrans extérieurs. Les calculs sont effectués en utilisant les théories de Ptolémée. La figure ci-dessous nous montre une des pages dédiées au calcul des éclipses de Lune. On y voit la Lune, les cônes d'ombre et de pénombre de la Terre représentés avec des proportions assez bonnes.
Difficilement décelable à l'œil nu les éclipses de Lune par la pénombre ne seront pas observées avant l'apparition de la lunette astronomique, il convient malgré tout de signaler l'observation d'une éclipse par la pénombre par les Babyloniens le 1 août -187 (188 av. J.-C.). Une étude des observations des éclipses de Lune publiées par les chroniqueurs arabes médiévaux faite par Said et Stephenson en 1991 montre que l'on a des observations à l'œil nu d'éclipses partielles par l'ombre jusque des grandeurs de 0,28 et de 0,12.
Les éclipses anciennes
Les Babyloniens surent prédire la date et la visibilité des éclipses de Lune relativement tôt, on dispose d'un texte datant du règne de Ukin-zer (731 av. J.-C. - 729 av. J.-C.) où figure la prédiction de l'éclipse de Lune du 9 avril -730 avec la mention de son invisibilité à Babylone. On distingue deux types de sources, les éclipses babyloniennes décrites par Ptolémée dans l'Almageste, elles sont au nombre de dix :
| Date de l'éclipse |
Type de l'éclipse |
| 19 mars - 720* |
Totale (1,49) |
| 8 mars - 719* |
Partielle (0,08) |
| 1 septembre - 719 |
Partielle (0,46) |
| 22 avril - 620 |
Partielle (0,18) |
| 16 juillet - 522 |
Partielle (0,56) |
| 19 novembre -501* |
Partielle (0,22) |
| 25 avril - 490 |
Partielle (0,12) |
| 23 décembre - 382* |
Partielle (0,23) |
| 18 juin - 381* |
Partielle (0,51) |
| 12 décembre - 381* |
Totale (1,50) |
(*) Ces observations ont été utilisées par Ptolémée pour calculer les variations de l'anomalie de la Lune. En plus de ces observations, Ptolémée donne six autres observations d'éclipses de Lune dont cinq ont été faites à Alexandrie et une à Rhodes.
L'autre source d'observations d'éclipses de Lune par les Babyloniens est constituée de textes cunéiformes. On y dénombre une soixantaine d'éclipses réparties entre 695 av. J.-C. et 67 av. J.-C.
Les données d'observations d'éclipses de Lune par les Chinois sont plus tardives, elles sont réparties entre l'an 434 et l'an 1280, les données d'observations d'éclipses de Lune par les Arabes sont comprises entre l'an 854 et l'an 1019. La totalité de ces observations a été utilisée, avec les observations d'éclipses de Soleil, pour déterminer les écarts entre le Temps universel et le Temps terrestre durant les siècles passés.
Quelques éclipses historiques
L'éclipse d'Alexandre
Cette éclipse totale de Lune (m =1,23) eu lieu le 20 septembre -330 (331 av. J.-C.), à l'époque des combats entre Alexandre le Grand et les forces perses de Darius III, à Gaugamèles près d'Arbèles. La vue de cette éclipse aurait désorganisé les forces perses et permis la victoire d'Alexandre 11 jours plus tard (Plutarque,Vie d'Alexandre, Livre XXXI). Cette éclipse est également mentionnée par Pline l'Ancien (23 - 79 ap. J.-C.) dans son Histoire Naturelle (Livre II), selon Pline cette éclipse fut également visible en Sicile au lever du Soleil alors qu'elle a eu lieu la nuit à Arbèles. Pline utilise ce décalage horaire pour prouver que la Terre est ronde. L'éclipse d'Alexandre est également décrite par Arrien de Nicomédie (v. 95 - v. 175) dans L'Expédition d'Alexandre ou Anabase (Livre II) ; il situe la bataille d'Arbèles au mois de Pyaneptiôn lorsque Aristophane était Archonte d'Athènes. Une autre description intéressante de l'éclipse est celle donnée par Quinte-Curce (Ier s. apr. J.-C.) dans son Histoire d'Alexandre le Grand (Livre IV). C'est, en effet, une des plus anciennes allusions à l'aspect rougeâtre des éclipses totales de Lune.
L'éclipse de la chute de Constantinople
Cette éclipse partielle de Lune (m= 0,746) eu lieu le 22 mai de l'an 1453, elle mit fin au siège de Constantinople par les troupes turques du Sultan Mohammed II. La ville est vaillamment défendue par l'empereur Constantin Dragasès (1448-1453) et le Génois Giustiniani, une ancienne prophétie affirmait que la ville ne pourrait tomber qu'à la Lune croissante, alors qu'ils avaient déjà repoussé trois assauts avec succès et confiance, le lever de la pleine Lune éclipsée démoralisa les assiégés. La ville fut prise le 29 mai, sept jours plus tard. Cette victoire des Turcs sur les forces chrétiennes marque la fin de l'empire byzantin et le début de l'empire ottoman.
L'éclipse de Colomb
Cette éclipse totale de Lune (m=1,097) eu lieu le 29 février de l'an 1504. Lors de son quatrième voyage Christophe Colomb, échoua sur les côtes de la Jamaïque. Suite à la mutinerie d'une partie de son équipage qui déroba une partie de ces réserves, Christophe Colomb se trouva à court de vivres, les indiens refusant de l'approvisionner. Christophe Colomb prédit aux indiens une éclipse totale de Lune trois jours avant sa venue et la présenta comme un signe céleste du mécontentement du Dieu des chrétiens. L'éclipse eu lieu effectivement la nuit du 29 février est fut, nous dit Christophe Colomb, d'un rouge sombre. Fortement impressionnés par ce phénomène céleste, les indiens ravitaillèrent Christophe Colomb et son équipage jusqu'à l'arrivée des secours, quatre mois plus tard. Christophe Colomb ne cite pas ses sources pour la détermination de cette éclipse. À cette époque trois sources étaient possibles : les éphémérides et Calendarium de Regiomontanus (pour Nuremberg), l'Almanach Perpetuum d'Abraham Zacuto (pour Salamanque) et enfin le Lunarium de Bernard Granollachs (pour Barcelone). Christophe Colomb a vraisemblablement utilisé le Calendarium de Regiomontanus. La Lune se lève éclipsée, C. Colomb va mesurer la durée de l'éclipse, cinq sabliers depuis le coucher du Soleil, et va en déduire la longitude du lieu. Dans le calcul de cette longitude, il va commettre une erreur importante de 37°.
Rotondité de la Terre
Aristote (384 - 322 av. J.-C.) dans le Traité du ciel (Livre II, 13) nous informe que les Pythagoriciens, notamment Philolaos (~470 - ~390 av. J.-C.), avaient observé qu'il y avait plus d'éclipses de Lune que d'éclipses de Soleil, ils avaient expliqué ce phénomène en supposant l'existence d'une seconde Terre, l'anti-Terre, située à l'opposé de la Terre par rapport à un feu central et qui venait s'interposer entre le Soleil et la Lune. Cette anti-Terre n'était donc pas visible de la Terre et doublait le nombre d'éclipse de Lune. Cette explication, bien qu'étonnée, prouve que les Pythagoriciens avaient bien compris le mécanisme des éclipses, notamment que les corps célestes sont sphériques et que certains sont lumineux et d'autres plus ou moins opaques.
L'observation des éclipses de Lune a été utilisée par Aristote pour prouver que la Terre était ronde, ainsi dans le Traité du ciel (Livre II, 14) on peut lire "Lors des éclipses, la Lune a toujours pour limite une ligne courbe : par conséquent, comme l'éclipse est due à l'interposition de la Terre, c'est la forme de la surface de la Terre qui est cause de la forme de cette ligne". On remarquera que cette preuve n'est pas suffisante pour prouver la sphéricité de la Terre, un cylindre et un disque ont également des ombres circulaires. Le dessin ci-dessous, qui illustre la démonstration d'Aristote, est extrait de la Cosmographie de Petrus Apianus (1581).

Crédit : Bibliothèque de l'Observatoire de Paris
Le calcul de la distance Terre-Lune
Introduction
 Introduction
Introduction
Cette dernière section est purement mathématiques, elle présente un des calculs effectués par Aristarque de Samos dans son traité sur la grandeur et la distance du Soleil et de la Lune. Puis nous étudions les deux observations effectuées par Ptolémée et décrites dans l'Almageste, ces observations permettent de calculer le diamètre apparent de la Lune, puis les distances Terre-Lune et Terre-Soleil. On compare à cette occasion les valeurs calculées par Ptolémée avec les valeurs actuelles.
Par Aristarque de Samos
Aristarque de Samos (310 - 230 av. J.-C.) fut l'élève de Straton de Lampsaque, il est l'auteur du premier système héliocentrique, système décrit dans son livre "Les Hypothèses" (disparu) cité par Archimède dans son traité de l'Arénaire. Aristarque est également l'auteur du traité sur la grandeur et la distance du Soleil et de la Lune.
Pour le calcul des distances Terre-Lune et Terre-Soleil, il fait les hypothèses suivantes :
- 1. La Lune reçoit la lumière du Soleil.
- 2. La Terre peut être considérée comme un point et comme le centre de l'orbite de la Lune.
- 3. Lorsque la Lune nous parait dikhotome (coupée en deux portions égales), elle offre à nos regards son grand cercle, qui détermine la partie éclairée et la partie obscure de cet astre.
- 4. Lorsque la Lune nous parait dikhotome, sa distance du Soleil est moindre du quart de la circonférence, de la trentième partie de ce quart.
- 5. La largeur de l'ombre est de deux Lunes.
- 6. L'arc soutendu dans le ciel par la Lune est la quinzième partie d'un signe.
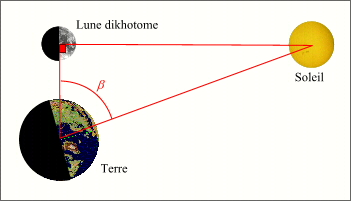
L'hypothèse 4 d'Aristarque
Crédit : IMCCE/Patrick Rocher
Comme on le constate certaines de ces hypothèses sont fausses, l'hypothèse 4 revient à donner à l'angle β la valeur de 87°. Cette erreur explique son l'erreur sur le calcul de la distance Terre-Soleil. L'hypothèse 6 donne à la Lune un diamètre de 2°, valeur quatre fois trop forte.
À partir de ces hypothèses, Aristarque va déduire que la distance Soleil-Terre est supérieure à 18 fois la distance Terre-Lune et inférieure à 20 fois la distance Terre-Lune. Il déduit de ces proportions les valeurs suivantes :
- le diamètre lunaire est inférieur à 2/45 distance Terre-Lune et supérieur à 1/30 distance Terre-Lune.
- le diamètre solaire est inférieur à 43/6 diamètres terrestres et supérieur à 19/3 diamètres terrestres.
- le diamètre terrestre est inférieur à 60/19 diamètres lunaires et supérieur à 108/43 diamètres lunaires.
 Remarque
Remarque
Il convient de remarquer qu'à l'époque d'Aristarque les Grecs n'avaient aucune notion de trigonométrie, les premières tables de cordes sont attribuées à Hipparque. C'est pourquoi Aristarque ne tire pas directement la valeur du rapport des distances Terre-Lune et Terre-Soleil de l'angle β, mais encadre cette proportion grâce à des considérations purement géométriques.
On trouve dans la littérature et sur le web de nombreux "exemples" de la détermination de la distance Terre-Lune par Aristarque, avec des hypothèques qui sont très variées (ombre cylindrique, ombre de trois diamètres lunaires, diamètre apparent de la Lune égal à 30'....) et utilisant des méthodes trigonométriques. C'est fort dommage car les méthodes employées par Aristarque sont remarquables et ont un intérêt pédagogique certain.
On peut consulter, sur le site Gallica (gallica.bnf.fr) de la Bibliothèque Nationale, une version française du Traité d'Aristarque de Samos Sur les grandeurs et les distances du Soleil et de la Lune traduite du grec par le Comte de Fortia d'Urban et édité en 1823.
On trouve dans un passage d'Archimède qu'Aristarque a également utilisé la valeur d'une demi-degré pour le diamètre lunaire, l'usage de la valeur de 2° dans le traité Sur la grandeur et la distance du Soleil et de la Lune est parfois présenté comme une valeur hypothétique utilisée par l'auteur dans une démonstration qui se veut plus didactique que physique.
En savoir plus: Une des démonstrations d'Aristarque
 En savoir plus
En savoir plus
La démonstration suivante est issue de la traduction du Comte de Fortia d'Urban et se trouve dans la proposition VIII du Traité d'Aristarque. Pour rendre la démonstration plus lisible je l'ai retranscrite en termes mathématiques plus contemporains.
La proposition
La proposition VIII est la suivante : La distance à laquelle le soleil se trouve de la terre est plus grande dix-huit fois, mais moindre vingt fois que celle à laquelle la lune se trouve de la terre.
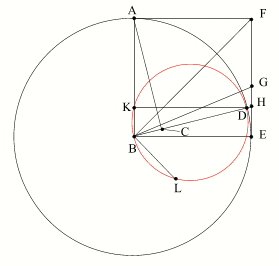
Crédit : IMCCE/Patrick Rocher
La démonstration
Soit A le centre du Soleil, B le centre de la Terre et C le centre de la Lune. Traçons le cercle (c) de centre B et de rayon AB, le rayon BD passant par C et faisant un angle de 3° avec le rayon BE perpendiculaire à BA (l'angle CBE est la trentième partie de l'angle droit). On construit le carré ABEF, ainsi que sa diagonale BF. Soit BG la bissectrice de l'angle EBF.
L'angle CBE est la trentième partie d'un angle droit (90°/30) et l'angle GBE est le quart d'un angle droit (90°/4), donc l'angle GBE vaut les 15/2 de l'angle CBE. Le rapport de EG sur EH est plus grand que le rapport des deux angles GBE et CBE, donc plus grand que 15/2.
BF est la diagonale du carré ABEF, donc le carré de BF est le double du carré de BE. De plus le carré construit sur FG est aussi le double du carré construit sur EG.
Or comme 49 est inférieur au double de 25, le carré de FG/EG = 2 est supérieur à 49/25, le rapport FG/EG est donc supérieur à 7/5.
Donc EF/EG = (EG+GF)/EG = 1 + GF/EG est supérieur à 12/5 ou 36/15.
Ainsi EG/EH est plus grand que 15/2 et EF/EG est supérieur à 36/15, donc EF/EH est supérieur à 18.
Or EF = BE, donc BE/EH est supérieur à 18, et comme BH est supérieur à BE, BH/EH est également supérieur à 18. Or les triangles ABC et EBH sont semblables, donc les rapports BH/EH et AB/BC sont égaux et l'on a bien BA supérieur à 18 BC.
La distance Terre-Soleil est supérieure à 18 fois la distance Lune-Soleil.
Reste à prouver que ce rapport est inférieur à 20. Pour cela traçons la parallèle à BE, cette parallèle coupe AB en K. Traçons le cercle passant par les points BDK et soit L le point du cercle tel que LB soit le côté d'un hexagone inscrit dans ce cercle.
L'angle DBK est égal à l'angle DBE égal à la trentième partie d'un angle droit, l'arc de cercle BK vaut le double donc la quinzième partie d'un angle droit ou encore la soixantième partie de la circonférence.
Or BL est la sixième partie de cette même circonférence; donc l'arc BL est dix fois plus grand que l'arc BK. Or le rapport des cordes BL/BK est inférieur au rapport des arcs BL/BK, donc la corde BL est inférieure à dix fois la corde BK.
Or BD est égal à deux BL, donc BD est inférieur à 20 BK. Or les triangles DKB et ABC sont semblables donc BD/BK = AB/BC, donc AB est bien inférieur à 20 BC.
 Remarque
Remarque
Bien évidemment, si l'on connaît la trigonométrie, cette longue démonstration élégante est remplacée par une simple équation à savoir : AB/BC = 1/sin 3° d'où AB/BC = 19,10.
Par Claude Ptolémée
Ptolémée, dans l'Almageste (livre V chapitre 14), nous décrit deux méthodes permettant de calculer le diamètre apparent de la Lune, puis les distances Terre-Lune et Terre-Soleil.
Le calcul du diamètre lunaire
Pour le calcul du diamètre apparent de la Lune, Ptolémée utilise deux éclipses de Lune observées à Babylone. La première a eu lieu l'an 5 de l'ère de Nabopolassar, qui est l'année 127 de l'ère de Nabonassar, à la fin de la onzième heure du 27 au 28 du mois égyptien Athyr (troisième mois de l'année). Cette date correspond à la nuit du 21 au 22 avril -620 (621 av. J.-C.). Ptolémée nous dit "on vit à Babylone la Lune commencer à s'éclipser; et la plus grande phase de cette éclipse fut du quart du diamètre dans la partie méridionale de l'astre". Puis il calcule la position de la Lune sur son orbite pour l'instant du maximum de l'éclipse et trouve qu'elle se trouve à 9,5° de son nœud et que la distance angulaire entre le centre de la Lune et le centre de l'axe des cônes est de 48,5'. La seconde éclipse de Lune utilisée est celle de l'an 7 de Cambyse, c'est-à-dire l'an 225 de l'ère de Nabonassar, elle s'est produite à une heure avant minuit du 17 au 18 du mois égyptien Phamenoth, ce qui correspond à l'éclipse du 16 juillet -522 (523 av. J.-C.); Ptolémée nous dit "on vit à Babylone la lune s'éclipser de la moitié de son diamètre dans la partie boréale" et il calcule qu'au maximum de l'éclipse la Lune est à 7,8° de son nœud et que la distance angulaire entre le centre de la Lune et le centre de l'axe des cônes est de 40,6'. Ptolémée calcule également que les deux éclipses ont lieu sensiblement lorsque la Lune est à une même distance angulaire de son apogée, donc que les diamètres lunaires apparents sont sensiblement identiques, alors la différence des distances à l'axe des cônes est égale au quart de diamètre lunaire, Ptolémée en déduit que le diamètre lunaire est de l'ordre de 31,3'. À partir de la deuxième éclipse, Ptolémée calcule également le rayon du cône d'ombre en fonction du rayon apparent de la Lune et il trouve que ce rayon "est un peu moindre que le double et 3/5 du rayon de la Lune".
Les tableaux suivants donnent les valeurs calculées avec les théories actuelles et les valeurs données par Ptolémée dans l'Almageste.
L'éclipse des 21 et 22 avril -620
|
Valeurs calculées actuelles |
Valeurs données par Ptolémée |
| Magnitude |
0,1818685 |
|
| Diamètre lunaire apparent |
29,51' |
|
| Instant du maximum |
1h56,2m UT |
|
| Instant du maximum en heure locale |
4h54,2m |
environ 6 h |
| Distance centre de la Lune axe des cônes |
48'31,91" |
48'30" |
| Longitude de la Lune |
204°53'31,5" |
205°32' |
| Elongation par rapport au noeud |
8,77° |
9,3° |
| Longitude par rapport à l'apogée |
339°6' |
340°7' |
L'éclipse du 16 juillet -522
|
Valeurs calculées actuelles |
Valeurs données par Ptolémée |
| Magnitude |
0,5615770 |
|
| Diamètre lunaire apparent |
29,63' |
|
| Instant du maximum |
20h28,8m UT |
|
| Instant du maximum en heure locale |
23h26,8m |
environ 23h |
| Distance centre de la Lune axe des cônes |
37'21,56" |
40'40" |
| Longitude de la Lune |
287°0'41,68" |
288°14' |
| Elongation par rapport au noeud |
6,75° |
7,8° |
| Longitude par rapport à l'apogée |
31°55' |
28°5' |
Ptolémée garde cette valeur de 31' 20" pour le diamètre lunaire et la considère comme constante alors qu'il tient compte des variations de la distance Terre Lune. Il estime le maximum de cette distance à 64 +1/6 rayons terrestres. La valeur moyenne étant de 59 rayons terrestres et il représente le mouvement de la Lune à l'aide d'un cercle déférent de 59 rayons terrestres et d'un épicycle de 5 +1/6 rayons terrestres. En faisant l'hypothèse que le diamètre apparent du Soleil est égal au diamètre apparent de la Lune à son apogée, il déduit de ces valeurs la distance Terre-Soleil et la distance de la Terre au sommet de son cône d'ombre. Il trouve une distance Terre Soleil de 605 rayons terrestres et une distance Terre sommet du cône d'ombre de 134 rayons terrestres.
 Introduction
Introduction Prérequis
Prérequis



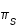
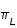
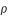
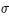

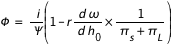


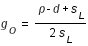
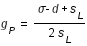
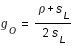 .
.









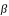 : la différence des latitudes entre la Lune et le centre du cône d'ombre à l'instant de l'opposition.
: la différence des latitudes entre la Lune et le centre du cône d'ombre à l'instant de l'opposition.
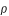 (et de pénombre
(et de pénombre 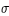 ) et du demi-diamètre de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore :
) et du demi-diamètre de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore :
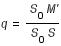 soit
soit 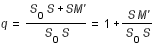
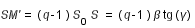 avec
avec 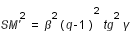
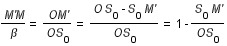
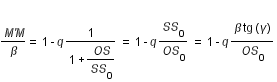
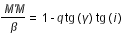
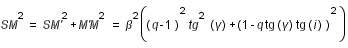 (1)
(1)
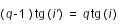
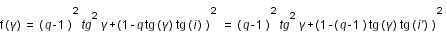
 est minimum lorsque
est minimum lorsque 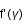 est nulle
est nulle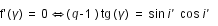 (2)
(2)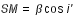 (3)
(3)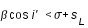
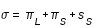
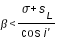 (4)
(4)
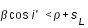
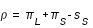
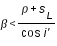 (5)
(5)
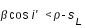
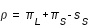
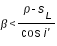 (6)
(6)
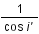
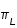
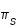
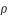 *
*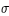 *
*