Le critère en latitude

On démontre qu'une éclipse de Lune se produira si, au moment de la pleine Lune (instant où la différence des longitudes géocentriques de la Lune et du Soleil est égale à 180°, c'est-à-dire au moment de l'opposition), la valeur absolue de la différence b des latitudes géocentriques apparentes du centre de la Lune et du centre du cône d'ombre est inférieure à 1,41° (1° 25' 23"), elle se produira peut-être si elle est comprise entre 1,41° (1° 25' 23") et 1,59° (1°35' 40") et elle ne se produira pas si elle est supérieure à 1,59° (1° 35' 40").

Critères en latitude pour les éclipses de Lune (vue depuis la Terre)

Crédit : IMCCE/Patrick Rocher

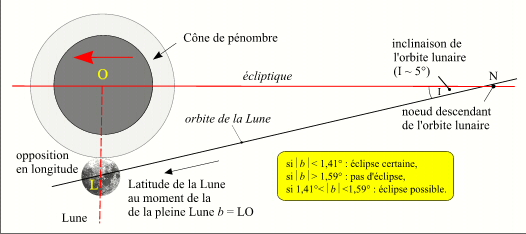
Sur la figure ci-dessus, la distance minimale correspond à l'instant où pour le centre de la Terre, le centre de la Lune est le plus près possible du centre du cône d'ombre, cela correspond si l'éclipse a lieu, au maximum de l'éclipse. Durant une éclipse de Lune on a toujours un des deux scénarios suivants :

• si l'éclipse a lieu avant le passage de la Lune au nœud, on observe d'abord l'opposition (pleine Lune), puis le maximum de l'éclipse, puis le passage au nœud,
• si l'éclipse a lieu après le passage de la Lune au nœud, on observe d'abord le passage au nœud, puis le maximum de l'éclipse et enfin l'opposition.

La géométrie de ce dessin montre également que plus l'opposition est proche du nœud, plus la distance minimale entre la Lune et le centre du cône d'ombre est petite et plus la grandeur (magnitude) de l'éclipse est grande. Ainsi, les éclipses par la pénombre correspondent à des oppositions situées loin des nœuds de l'orbite lunaire et les éclipses par l'ombre (partielles ou totales) correspondent à des oppositions proches des nœuds de l'orbite lunaire.

On peut détailler le critère en latitude en déterminant pour quelle valeur de b (0,89°) on a une éclipse par l'ombre avec certitude et pour quelle valeur de b (1,06°) on n'a pas d'éclipse par l'ombre avec certitude (mais une éclipse par la pénombre avec certitude); de même on peut déterminer pour quelle valeur de b (0,36°) on a une éclipse totale avec certitude et pour quelle valeur de b (0,53°) on n'a pas d'éclipse totale avec certitude, ces valeurs sont données dans le graphique ci-dessous.

Crédit : IMCCE/Patrick Rocher

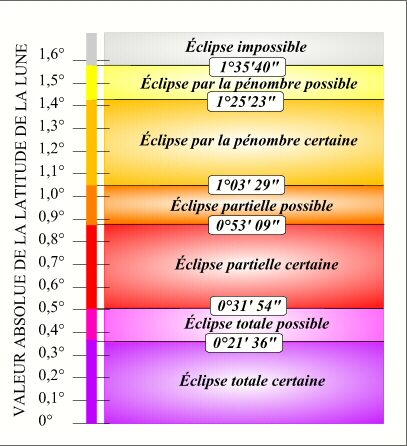
On peut également calculer les valeurs moyennes de ces critères en latitude. Pour avoir une éclipse de Lune par la pénombre il faut que b soit inférieure à β_m = 1,49°, pour avoir une éclipse de Lune par l'ombre il faut que b soit inférieure à β_m = 0,96° et pour avoir une éclipse totale de Lune il faut que b soit inférieure à β_m = 0,44°. Ces valeurs moyennes permettent de calculer également la proportion d'éclipses par la pénombre (36%), la proportion d'éclipses par l'ombre (64%) et la proportion d'éclipses totales (30%).