 |  |  |  |  |  |
Soleil Terre Lune Phénomènes Les éclipses de LuneEn savoir plus: La démonstration du critère en latitude |
En savoir plusLa démonstration est en tout point identique à la démonstration du critère en latitude des éclipses de Soleil, il suffit de remplacer la conjonction par l'opposition et le Soleil par les cônes d'ombre et de pénombre de la Terre.
Nous allons établir le critère en latitude dans le cas d'une éclipse au nœud ascendant de l'orbite lunaire, l'opposition ayant lieu avant le passage au nœud. La démonstration est identique pour un passage au nœud descendant ou avec une opposition située après le passage au nœud, la seule chose qui change dans ce dernier cas est la position du minimum de distance entre des deux corps.
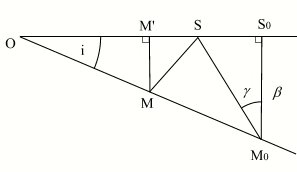
Soit M0 et S0 : les positions de la Lune et du centre du cône d'ombre à l'instant de l'opposition (pleine Lune) avant le passage de la Lune au nœud ascendant de son orbite.
M et S : les positions de la Lune et du centre du cône d'ombre à un instant t postérieur à l'opposition.
γ : l' angle S0M0S.
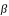: la différence des latitudes entre la Lune et le centre du cône d'ombre à l'instant de l'opposition.
q : le rapport du mouvement en longitude de la Lune sur celui du centre du cône d'ombre (Soleil+180°).
Le calcul du critère en latitude consiste à calculer le minimum de la distance SM et de le comparer à la somme des demi-diamètres géocentriques apparents des cônes d'ombre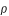 
(et de pénombre 
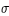) et du demi-diamètre de la Lune. SM se calcule simplement en utilisant le théorème de Pythagore :
On a :
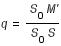soit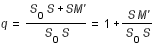 
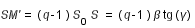avec 
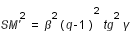
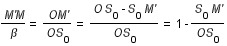
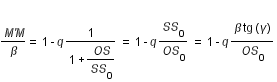
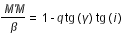
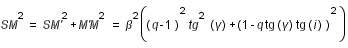(1)
On introduit un angle auxiliaire i', tel que :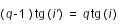 
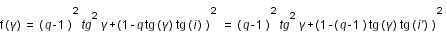
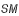est minimum lorsque 
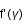est nulle
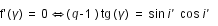(2)
Ce qui correspond à :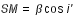 
(3)
Cette distance correspond à une observation vue du centre de la Terre (coordonnées géocentriques).
 |  |