En savoir plus: La démonstration du critère en latitude-2

En savoir plus

Il y a éclipse par la pénombre lorsque SM est inférieur à la somme des demi-diamètres apparents du cône de pénombre et de la Lune.

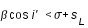
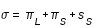
soit : 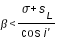   (4)

Il y a éclipse par l'ombre lorsque SM est inférieur à la somme des demi-diamètres apparents du cône d'ombre et de la Lune.

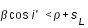
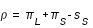
soit : 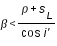   (5)

Il y a éclipse totale par l'ombre lorsque SM est inférieur à la différence des demi-diamètres apparents du cône d'ombre et de la Lune.

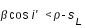
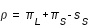
soit : 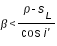   (6)

Il suffit alors de remplacer dans ces formules les paramètres par leurs valeurs extrêmes pour en déduire les critères en latitude.

Le tableau suivant donne les valeurs extrêmes des paramètres, l'étude des séries donnant l'orbite de la Lune, montre qu'au voisinage de la nouvelle Lune (et de la pleine Lune) la valeur de l'inclinaison est maximale, il convient donc de prendre i ~ 5° 17' dans ces formules.

	maximum	Minimum	moyenne
q	16,2	10,9	13,5
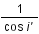
	1,0052	1,0043	1,00472
Parallaxe Lune	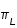61' 27"	53' 53"	57' 2,70"
Parallaxe Soleil	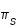8,96"	8,65"	8,80"
1/2 diamètre Lune sL	16' 45"	14' 41"	15' 32,58"
1/2 diamètre Soleil sS	16' 18"	15' 46"	15' 59,63"
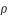*	46' 27"	38' 15"	41' 45,73"
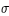*	1° 18' 30"	1° 10' 20"	1° 13' 45"

* Dans le calcul de ces valeurs on a tenu compte de la réfraction atmosphérique et de la parallaxe de la Lune à 45° de latitude en multipliant σ par (1+1/128) et ρ par (1+1/73).

Ainsi la valeur inférieure β_Min du second membre de (4) est obtenue avec σ et s_L minimales, la valeur supérieure β_Max est obtenue avec σ et s_L maximales et l'on obtient β_Min=1°25'23" et β_Max=1°35'40". Ce sont les limites d'existence des éclipses de Lune.

De même la valeur inférieure β_Min du second membre de (5) est obtenue avec ρ et s_L minimales, la valeur supérieure β_Max est obtenue avec ρ et s_L maximales et l'on obtient β_Min=0°53'9,63" et Δ_Max=1°3'28,6". Ce sont les limites d'existence des éclipses de Lune par l'ombre.

Et enfin la valeur inférieure β_Min du second membre de (6) est obtenue avec ρ minimal et s_L maximal, la valeur supérieure β_Max est obtenue avec ρ maximal et s_L minimal et l'on obtient β_Min=0°21'35,52" et β_Max=0°31'54,52". Ce sont les limites d'existence des éclipses totales de Lune.