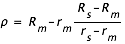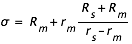Introduction
Introduction
Dans cette section, nous allons préciser la taille et la vitesse des l'intersections des cônes d'ombre et de pénombre avec la surface de la Terre. Puis nous définirons des paramètres caractéristiques des éclipses de Soleil : la magnitude et le degré obscuration.
Les tailles
Le dessin ci-contre est trompeur, en effet nous avons représenté les trois corps sur la même figure et cela introduit, comme nous l'avons déjà signalé, des erreurs dans la taille des angles. Ainsi l'angle au sommet du cône de pénombre est de l'ordre du demi-degré. De même, le Soleil étant très loin, les tangentes T1 (extérieure) et T2 (intérieure) sont quasi-parallèles, donc le rayon d'une section normale au cône de pénombre au niveau de la Terre est très proche du diamètre de la Lune, donc le diamètre de la section normale du cône de pénombre au niveau de la Terre est de l'ordre de deux diamètres lunaires, soit environ 7000 km. Ainsi la pénombre ne recouvre jamais entièrement la surface terrestre, mais uniquement 16% d'un demi-hémisphère terrestre.
La taille du diamètre de la section normale au cône d'ombre au niveau de la Terre dépend des distances Terre-Lune et Soleil-Lune, on montre, à l'aide des valeurs extrêmes de ces distances que le diamètre de la section normale au cône d'ombre pour une éclipse totale est au maximum de 268 km et que le diamètre de la section normale au prolongement du cône d'ombre pour une éclipse annulaire est au maximum de 375 km. Bien évidemment l'ombre et le prolongement de l'ombre coupent la surface de la Terre suivant un ovale (intersection d'un cône et d'une sphère) dont le grand axe peut dépasser largement ces valeurs extrêmes, c'est le cas notamment pour les éclipses rasantes (proches des pôles).
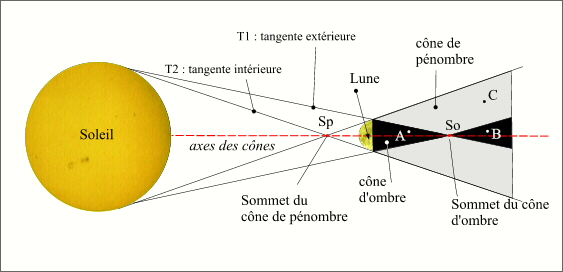
Différents types d'éclipses en fonction de la position de l'observateur.
Crédit : IMCCE/Patrick Rocher
Les vitesses
La vitesse à laquelle se déplace l'ombre où le prolongement de l'ombre sur la surface de la Terre est la combinaison de deux mouvements : le mouvement de l'ombre dans l'espace qui est égal au mouvement de la Lune par rapport au Soleil vu depuis la Terre fixe et le mouvement de la surface terrestre du à la rotation de la Terre sur elle-même. Depuis la Terre, le Soleil et la Lune se déplacent par rapport aux étoiles d'ouest en est (mouvement direct), la Lune se déplace environ treize fois plus vite que le Soleil, son ombre se déplace d'environ 1 km/s par rapport à la Terre supposée fixe. La Terre tourne sur elle-même également d'ouest en est. La vitesse de l'ombre par rapport au sol est donc égale à la différence de la vitesse de l'ombre de la Lune et de la vitesse du sol. À l'équateur la vitesse du sol est de l'ordre de 500 m/s, la différence des deux vitesses est de 500m/s, plus on s'écarte en latitude de l'équateur, plus la vitesse de l'ombre est grande pour atteindre 1 km/s aux pôles (vitesse du sol nulle).
 En savoir plus
En savoir plus
Vitesse de l'ombre à la surface d'une Terre fixe.
Crédit : IMCCE/Patrick Rocher
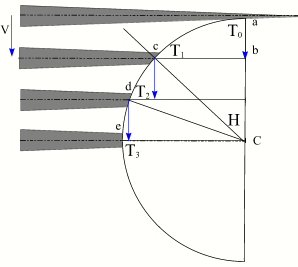
En réalité, le calcul de la vitesse de l'ombre à surface du sol est plus complexe, dans l'explication précédente nous avons fait des simplifications qui ne sont vraies que lorsque les vecteurs vitesses de l'ombre et du sol sont colinéaires. Dans un premier temps, on peut supposer une Terre fixe avec une ombre de la Lune se déplaçant avec une vitesse constante V par rapport à la Terre. Sur la figure ci-contre nous avons tracé la position du cône d'ombre et de son axe à des instants T0, T1, T2 et T3 séparés par un intervalle de temps dt constant. Durant le premier intervalle 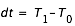 l'ombre de la Lune s'est déplacée de
l'ombre de la Lune s'est déplacée de 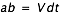 dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).
dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).
 En savoir plus
En savoir plus
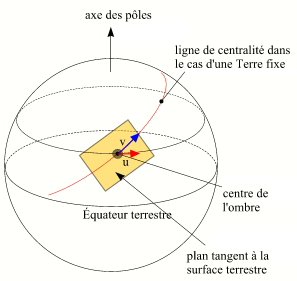
Combinaison des vitesses de l'ombre de la Lune et de la surface terrestre.
Crédit : IMCCE/Patrick Rocher
Pour avoir la vitesse, et la trajectoire, de l'ombre par rapport au sol dans le cas d'une Terre en rotation sur elle-même, il convient de combiner les deux mouvements. Si v est le vecteur vitesse de l'ombre (par rapport à la Terre fixe) dans le plan tangent au point de contact de l'axe du cône avec la surface terrestre et u le vecteur vitesse du sol dans le même plan, alors la vitesse de l'ombre par rapport au sol est égale à la différence des deux vecteurs vitesses (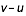 ). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.
). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.
 En savoir plus
En savoir plus
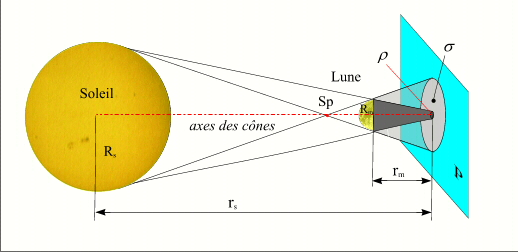
Éclipse totale : géométrie de l'ombre et de la pénombre dans un plan normal à l'axe des cônes.
Crédit : IMCCE/Patrick Rocher
Soit P un plan normal à l'axe des cônes d'ombre et de pénombre, ρ et σ les rayons des cercles définis par les intersections du cône de d'ombre et du cône de pénombre avec ce plan. Soit Rs le rayon solaire, Rm le rayon lunaire, rs et rm les distances respectives du centre du Soleil et du centre de la Lune au plan P. Une simple application du théorème de Thalès nous donne les valeurs de ρ et σ en fonction de Rs, Rm, rs et rm.
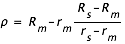
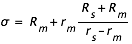
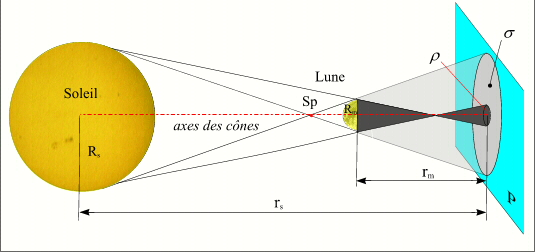
Éclipse annulaire : géométrie de l'ombre et de la pénombre dans un plan normal à l'axe des cônes.
Crédit : IMCCE/Patrick Rocher
Lorsque l'éclipse est annulaire le plan P coupe l'axe des cônes après le sommet du cône d'ombre, il coupe donc le prolongement du cône d'ombre. Les formules précédentes sont également applicables si l'on accepte que les rayons aient des valeurs négatives.
 En savoir plus
En savoir plus
Le tableau suivant donne les valeurs extrêmes de ρ et σ en fonction des distances Terre-Soleil et Terre-Lune. Dans le tableau on se place d'abord dans le plan du centre de la Terre, puis l'on se place à la surface de la Terre avec les deux corps au zénith, les distance Terre-Lune et Terre-Soleil sont alors diminuées d'un rayon terrestre, en fait, on néglige le rayon terrestre devant la distance Terre-Soleil. Dans ce tableau le rayon solaire est pris égal à Rs = 696 000 km, le rayon lunaire est pris égal à Rm = 1738,1 km et le rayon terrestre est pris égal à Re = 6400 km. Nous donnons également ρ et σ en secondes d'arcs, dans ce cas, ces valeurs représentent les rayons sélénocentriques (vu depuis le centre de la Lune) apparents des intersections des cônes d'ombre et de pénombre avec le plan P.
|
Périgée |
Moyenne |
Apogée |
| rm
|
357 200 km |
381 300 km |
407 000 km |
| rs
|
1,52 108 km |
1,50 108 km |
1,48 108 km |
|
ρ(km) |
104,9 km |
-34,7 km |
- 187,4 km
|
|
ρ(") |
60,5" |
-18,7 |
-94,8 km |
|
σ(km) |
3 379 km |
3 520 km |
3 673 km |
|
σ(") |
1948" |
1901" |
1859" |
| rm-Re
|
305 800 km |
374 900 km |
400 600 km |
|
ρ(km) |
134,1 km
|
-5.0 km |
-157 km |
|
ρ(") |
78,7" |
-2,8" |
-80,8" |
|
σ(km) |
3 350 km |
3 490 km |
3 643 km |
|
σ(") |
1966" |
1918" |
1873" |
Les valeurs extrêmes pour les éclipses périgées et apogées sont en italique et l'on retrouve bien les valeurs des diamètres de 268 km pour une éclipse périgée (donc totale) et de 375 km pour une éclipse apogée (donc annulaire). De même on constate que le diamètre de la pénombre qui est compris entre 6700 km et 7300 km est bien du même ordre de grandeur que deux diamètres lunaires.
Toutes les éclipses de Soleil ne sont pas identiques, il convient donc de trouver un paramètre qui les caractérise, ce paramètre est la grandeur ou la magnitude de l'éclipse, ces deux termes désignent la même quantité.
À un instant donné la grandeur g de l'éclipse est l'inverse du rapport du diamètre du Soleil sur la distance du bord du Soleil le plus rapproché du centre de la Lune au bord de la Lune le plus rapproché du centre du Soleil.
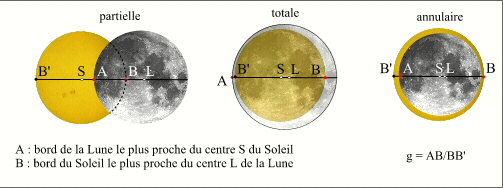
Grandeur ou magnitude d'une éclipses de Soleil.
Crédit : IMCCE/Patrick Rocher
Dans la figure ci-contre, nous avons ajouté une transparence à la Lune dans le cas de l'éclipse totale, cela permet de voir la position du Soleil. Comme on le constate sur la figure, les éclipses partielles et annulaires ont une grandeur inférieure à un et les éclipses totales ont une grandeur supérieure à un. Les éclipses mixtes ont une grandeur très proche de un. Pour les éclipses annulaires, plus la grandeur s'approche de un, plus le diamètre apparent de la Lune est proche du diamètre apparent du Soleil, donc plus l'éclipse est courte. Pour les éclipses totales, plus on s'écarte de un, plus le diamètre apparent de la Lune est grand par rapport au diamètre apparent du Soleil, donc plus l'éclipse est longue.
Le degré d'obscuration est aussi un paramètre caractéristique des éclipses de Soleil. Le degré obscuration est le pourcentage de la surface du disque solaire occulté par la Lune.
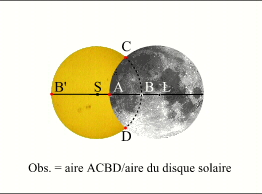
Le degré d'obscuration.
Crédit : IMCCE/Patrick Rocher
Le degré d'obscuration donne une information pour les éclipses annulaires et partielles car sa valeur est inférieure à 100%, par contre toutes les éclipses totales ont un degré d'obscuration de 100% quelle que soit la grandeur de l'éclipse.
La grandeur et le degré d'obscuration sont donnés dans les circonstances générales des éclipses, ce sont alors les valeurs maximales de ces paramètres sur toute la durée de l'éclipse, elles correspondent à un instant et un lieu bien défini sur la Terre : le lieu du maximum de l'éclipse (lieu sur la Terre où la grandeur est maximale) et l'instant où la grandeur est maximale en ce lieu. Ces deux valeurs sont également données dans les circonstances locales des éclipses, dans ce cas elles sont toujours inférieures ou égales (si on est au lieu du maximum) à celles données dans les circonstances générales.
 Introduction
Introduction

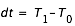 l'ombre de la Lune s'est déplacée de
l'ombre de la Lune s'est déplacée de 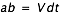 dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).
dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).

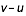 ). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.
). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.