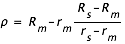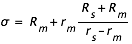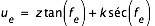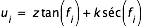Les éclipses de Soleil
Auteur: Patrick Rocher
- Introduction
- Les différents types d'éclipses
- Introduction
- Dimensions et distances des corps
- Le cône d'ombre et le cône de pénombre
- Les différents types d'éclipses du soleil
- Les éclipses non centrales
- Les éclipses centrales
- Les éclipses totales
- Les éclipses totales-2
- Les éclipses totales non centrales
- Les éclipses annulaires
- Les éclipses annulaires-2
- Les éclipses annulaires non centrales
- Les éclipses mixtes et les éclipses partielles
- Exercice
- La géométrie des éclipses de Soleil
- Introduction
- Caractéristiques des cônes d'ombre et de pénombre
- Caractéristiques des cônes d'ombre et de pénombre-2
- En savoir plus: Le calcul exact des vitesses : la vitesse de l'ombre à la surface terrestre
- En savoir plus: Le calcul exact des vitesses : combinaison des vitesses
- En savoir plus: Le calcul des rayons de l'ombre et de la pénombre
- En savoir plus: Le calcul des rayons de l'ombre et de la pénombre-2
- Magnitude ou grandeur d'une éclipse de Soleil
- Degré d'obscuration d'une éclipse
- Détermination des types d'éclipses en fonction des positions orbitales
- Introduction
- Diamètres apparents
- Positions orbitales
- Types d'éclipses en fonction des distances des corps
- Types d'éclipses en fonction des distances des corps-2
- Circonstances générales et cartes des éclipses
- Introduction
- Circonstances générales
- En savoir plus: Circonstances générales de l'éclipse des 10 et 11 juin 2002
- Les cartes d'éclipses
- En savoir plus: Exemple de carte générale en projection stéréographique
- En savoir plus: Exemple de carte en projection orthographique
- En savoir plus: Exemple de carte locale
- En savoir plus: Les différentes projections
- Circonstances locales des éclipses
- Introduction
- Circonstances locales éclipses totales
- Circonstances locales éclipses annulaires
- Circonstances locales éclipses partielles
- Circonstances locales angles au pole et au zenith
- Circonstances locales-5
- En savoir plus: Définition des éléments de Bessel
- En savoir plus: Définition des éléments de Bessel-2
- En savoir plus: Définition des éléments de Bessel-3
- En savoir plus: Définition des éléments de Bessel-4
- En savoir plus: Calcul des circonstances locales
- En savoir plus: Calcul de la grandeur maximale en un lieu
- En savoir plus: Calcul des instants des contacts en un lieu
- En savoir plus: Calcul de l'angle au pôle et de l'angle au zénith
Introduction
 Prérequis
Prérequis
Il est vivement conseillé de lire le cours sur les mouvements de la Terre et de la Lune.
 Introduction
Introduction
Nous présentons d'abord les aspects géométriques des éclipses, c'est-à-dire les positions relatives des corps et leur taille apparente. Ces différents aspects géométriques permettent de définir les types d'éclipses. Puis nous décrivons les différentes phases générales et locales des éclipses, ainsi que des méthodes de calcul permettant de les obtenir. Nous terminerons cette section avec les différentes représentations cartographiques des zones de visibilité des éclipses solaires.
Résumé
Les différents types d'éclipses, leur géométrie et enfin les circonstances générales et locales des éclipses solaires ainsi que leurs paramètres caractéristiques.
Les différents types d'éclipses
Introduction
 Introduction
Introduction
Dans cette section nous allons décrire les différents cas de figure qui peuvent se produire au moment de la conjonction entre la Lune et le Soleil. Nous en déduirons les différentes types d'éclipses de Soleil possibles selon que la Terre coupe ou ne coupe l'axe des cônes d'ombre ou de pénombre.
Dimensions et distances des corps
Le dessin ci-contre donne les rayons équatoriaux de la Terre, de la Lune et du Soleil, il donne également les distances moyennes entre ces corps, en kilomètres et en rayons terrestres. Comme on le constate, si l'on voulait réaliser un dessin comportant les trois corps il serait impossible de le faire à l'échelle. Ainsi si la Terre est représentée par un cercle de 2 cm de rayon, la Lune doit être représentée par un cercle de 0,55 cm situé à une distance d'environ 1,20 m de la Terre et si l'on voulait représenter le Soleil celui-ci aurait un rayon de 2,18 m et serait situé à 469 m de la Terre !
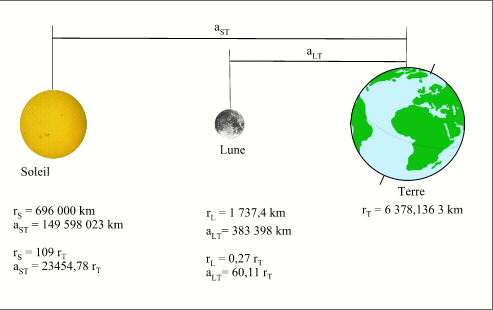
Crédit : IMCCE/Patrick Rocher
Aucun dessin représentant les trois corps n'est donc à l'échelle, et en ne respectant pas les distances et les tailles des corps, on introduit des distorsions dans les figures. Par exemple certaines droites quasi-parallèles se coupent suivant des angles qui sont beaucoup plus grands que la réalité.
Le cône d'ombre et le cône de pénombre
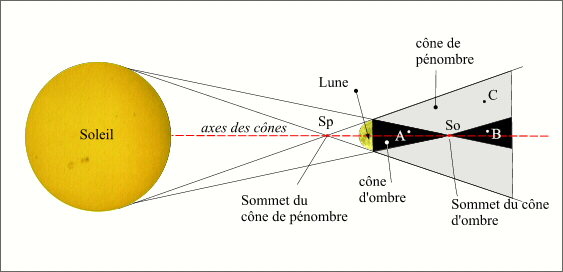
Cônes d'ombre et de pénombre
Crédit : IMCCE/Patrick Rocher
La Lune, éclairée par le Soleil, donne naissance, dans la direction opposée au Soleil à deux cônes, un cône d'ombre et un cône de pénombre. La droite joignant le centre du Soleil et le centre de la Lune constitue l'axe de ces cônes. Le sommet Sp du cône de pénombre est situé sur cet axe entre le Soleil et la Lune, et le sommet So du cône d'ombre est également situé sur cet axe mais de l'autre côté par rapport à la Lune. Le cône d'ombre est construit à l'aide des tangentes extérieures aux sphères solaire et lunaire, le cône de pénombre est construit à partir des tangentes intérieures aux sphères solaire et lunaire. Pour un observateur A placé dans le cône d'ombre, avant son sommet il y a éclipse totale du Soleil, pour un observateur B situé dans le prolongement du cône d'ombre, donc après le sommet du cône d'ombre, il y a éclipse annulaire du Soleil. Lorsqu'un observateur C se trouve dans le cône de pénombre, il assiste à une éclipse partielle, donc un passage partiel de la Lune devant le Soleil. En raison des variations de distances entre la Terre et la Lune, la Terre peut passer dans le cône d'ombre ou dans le prolongement du cône d'ombre.
Les différents types d'éclipses du soleil
Pas d'éclipse de Soleil
Souvent, au voisinage de la conjonction en longitude de la Lune et du Soleil (nouvelle Lune), au moment où la distance angulaire entre le centre de la Lune et le centre du Soleil vue depuis la Terre est minimale, la latitude de la Lune est trop grande et les cônes d'ombre et de pénombre ne rencontrent pas la surface terrestre. Alors, si la latitude de la Lune est positive, les cônes d'ombre et de pénombre passent au-dessus (au nord) de la Terre et si la latitude de la Lune est négative, les cônes d'ombre et de pénombre passent au-dessous (au sud) de la Terre. Dans ce cas il n'y a pas d'éclipse de Soleil.
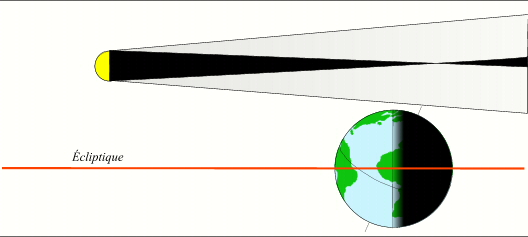
Pas d'éclipse de Soleil.
Crédit : IMCCE/Patrick Rocher
Les éclipses non centrales
Toujours au voisinage de la conjonction, lorsque l'axe des cônes d'ombre et de pénombre ne rencontrent pas la surface terrestre mais que le cône de pénombre et parfois également une partie du cône d'ombre rencontrent la Terre, il y a éclipse et l'on dit que l'éclipse est non centrale. On verra par la suite qu'une éclipse non centrale peut être totale, annulaire ou partielle.
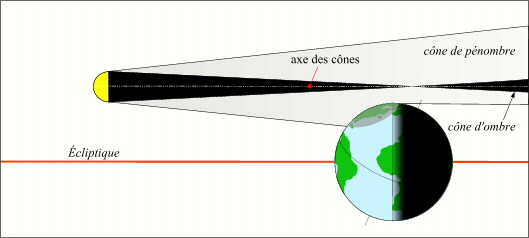
Éclipse non centrale.
Crédit : IMCCE/Patrick Rocher
Les éclipses centrales
Toujours au voisinage de la conjonction, lorsque l'axe des cônes d'ombre et de pénombre rencontre la surface terrestre, il y a éclipse et l'on dit que l'éclipse est centrale. On verra par la suite qu'une éclipse centrale peut être totale, annulaire ou mixte (annulaire-totale).
L'ensemble de la surface terrestre parcourue durant une éclipse par le cône d'ombre où par son prolongement porte le nom de bande de centralité. L'intersection de l'axe des cônes d'ombre et de pénombre avec la surface terrestre, lorsqu'elle existe (éclipses centrales) porte le nom de ligne de centralité.
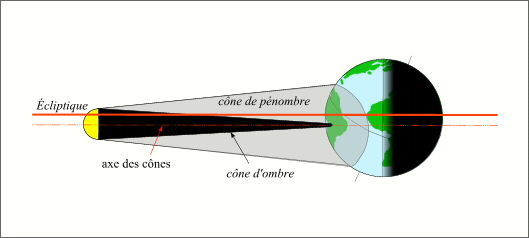
Éclipse centrale.
Crédit : IMCCE/Patrick Rocher
On remarquera que ces définitions portent uniquement sur la rencontre de l'axe des cônes d'ombre et de pénombre avec la surface terrestre.
Les éclipses totales
Lorsque la surface terrestre rencontre le cône d'ombre entre la Lune et le sommet du cône d'ombre, pour un observateur situé dans ce cône d'ombre la surface du Soleil est complètement occultée par la Lune, alors l'éclipse est dite totale. Le diamètre apparent de la Lune est supérieur au diamètre apparent du Soleil. La bande de centralité porte le nom de bande de totalité. Tous les observateurs situés sur cette bande de totalité observeront d'abord une phase partielle, puis la phase totale, puis de nouveau une phase partielle. Durant la phase de totalité la couronne solaire est observable. En début et en fin de phase de totalité un point brillant, appelé point de Baily, apparaît sur le limbe lunaire, ces points brillants proviennent de la lumière solaire passant par les vallées situées sur le limbe lunaire, ils annoncent le début et la fin de la phase de totalité.
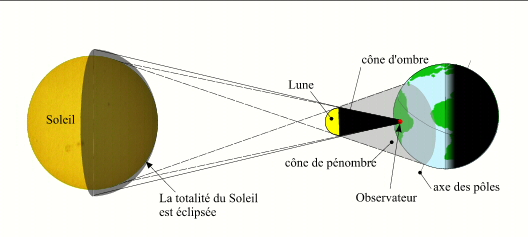
Éclipse totale centrale.
Crédit : IMCCE/Patrick Rocher

Photo de Christian Viladrich : éclipse totale du 26 février 1998.
Crédit : ASM
Les éclipses totales-2
Pour un observateur situé uniquement dans le cône de pénombre, une partie seulement du Soleil est occultée par la Lune, dans ce cas l'éclipse est vue par l'observateur sous la forme d'une éclipse partielle. Le diamètre apparent du Soleil est encore inférieur au diamètre apparent de la Lune.
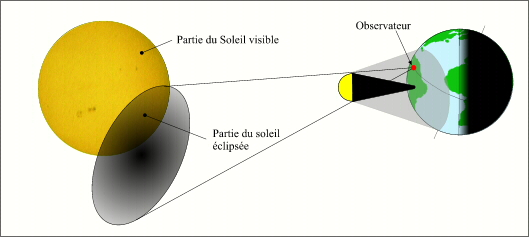
Phases partielles d'une éclipse totale.
Crédit : IMCCE/Patrick Rocher
Les éclipses totales non centrales
Il est possible que seule une petite partie du cône d'ombre rencontre la Terre sans que l'axe du cône d'ombre ne la rencontre. Dans ce cas, nous avons à faire à une éclipse totale non centrale, la bande de totalité est alors rasante à la surface de la Terre et la ligne de centralité n'existe pas. Sur la figure ci-contre, afin de la rendre plus lisible, nous avons ajouté une transparence au cône d'ombre pour voir que son axe ne rencontre pas la Terre, nous avons agrandi l'angle au sommet du cône d'ombre et nous avons supprimé le cône de pénombre.
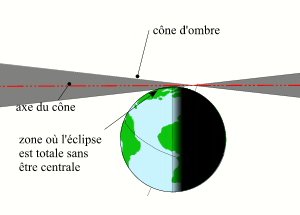
Éclipse totale non centrale.
Crédit : IMCCE/Patrick Rocher
Les éclipses annulaires
Lorsque la surface terrestre rencontre le prolongement du cône d'ombre, pour un observateur situé dans ce prolongement du cône d'ombre la surface du Soleil n'est pas complètement occultée par la Lune et le diamètre apparent de la Lune est plus petit que le diamètre apparent du Soleil. Dans ce cas l'éclipse est dite éclipse annulaire. Tous les observateurs situés sur la bande de centralité observeront d'abord une phase partielle, puis la phase annulaire, puis de nouveau une phase partielle. Lors des éclipses annulaires la couronne solaire n'est pas visible.
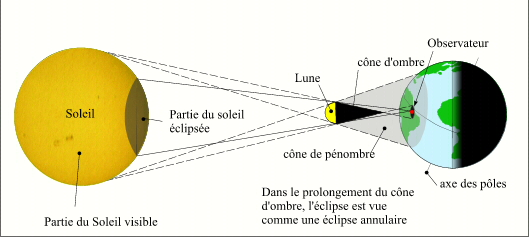
Éclipse annulaire centrale.
Crédit : IMCCE/Patrick Rocher

Phase annulaire.
Crédit : Christian Nitschelm
Les éclipses annulaires-2
Pour un observateur situé uniquement dans le cône de pénombre, une partie seulement du Soleil est occultée par la Lune. Dans ce cas l'éclipse sera vue par l'observateur sous la forme d'une éclipse partielle. Le diamètre apparent du Soleil est supérieur au diamètre apparent de la Lune.
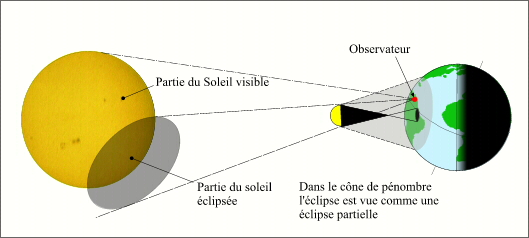
Phases partielles d'une éclipse annulaire.
Crédit : IMCCE/Patrick Rocher
Les éclipses annulaires non centrales
Comme pour les éclipses totales, il est possible que seule une petite partie du prolongement du cône d'ombre rencontre la Terre sans que l'axe du cône d'ombre ne la rencontre. Dans ce cas nous avons à faire à une éclipse annulaire non centrale, la bande de centralité est alors rasante à la surface de la Terre et la ligne de centralité n'existe pas. Sur la figure ci-contre, afin de la rendre plus lisible, nous avons ajouté une transparence au cône d'ombre pour voir que son axe ne rencontre pas la Terre, nous avons agrandi l'angle au sommet du cône d'ombre et nous avons supprimé le cône de pénombre.
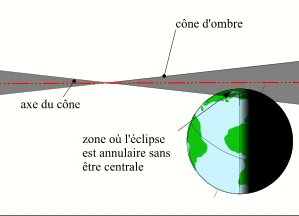
Éclipse annulaire non centrale.
Crédit : IMCCE/Patrick Rocher
Les éclipses mixtes et les éclipses partielles
Soit d la distance entre la projection normale P du centre de la Terre sur l'axe du cône d'ombre et le sommet So du cône d'ombre. Si d est inférieure au rayon terrestre r et si P est situé après le sommet du cône d'ombre, alors le premier contact entre la Terre et le cône d'ombre se fait dans le prolongement du cône d'ombre et l'éclipse débute par une éclipse annulaire, puis l'intersection de la Terre et du cône d'ombre se fait au sommet du cône d'ombre puis en avant du sommet du cône d'ombre, l'éclipse est alors totale, puis de nouveau l'intersection entre la Terre et le cône d'ombre se fait au sommet du cône, puis dans le prolongement du cône d'ombre. Donc au cours de son trajet sur la surface terrestre, l'éclipse est d'abord annulaire, puis totale, puis de nouveau annulaire. Ce type d'éclipse s'appelle éclipse mixte ou éclipse annulaire-totale.
Elle est également appelée éclipse perlée, en effet, durant ces éclipses le diamètre apparent de la Lune est toujours très proche du diamètre apparent du Soleil car l'intersection reste toujours au voisinage du sommet du cône d'ombre; or le limbe lunaire n'est pas un cercle parfait car il est constitué par une succession de montagnes et de vallées, chaque vallée laisse passer la lumière solaire et parsème le limbe lunaire de nombreux points de Baily donnant au limbe l'aspect d'un collier de perles. De plus comme l'intersection du cône d'ombre et de la Terre se fait toujours au voisinage du sommet du cône d'ombre, les éclipses perlées sont caractérisées par une bande de centralité très étroite.
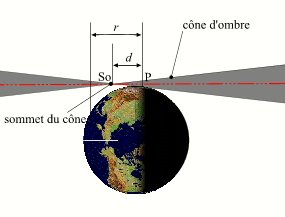
Géométrie des éclipses mixtes.
Crédit : IMCCE/Patrick Rocher
Les éclipses partielles
Enfin, lorsque la Terre rencontre uniquement le cône de pénombre de la Lune, seule une partie du Soleil est occultée et l'éclipse est dite partielle.
Exercice
La géométrie des éclipses de Soleil
Introduction
 Introduction
Introduction
Dans cette section, nous allons préciser la taille et la vitesse des l'intersections des cônes d'ombre et de pénombre avec la surface de la Terre. Puis nous définirons des paramètres caractéristiques des éclipses de Soleil : la magnitude et le degré obscuration.
Caractéristiques des cônes d'ombre et de pénombre
Les tailles
Le dessin ci-contre est trompeur, en effet nous avons représenté les trois corps sur la même figure et cela introduit, comme nous l'avons déjà signalé, des erreurs dans la taille des angles. Ainsi l'angle au sommet du cône de pénombre est de l'ordre du demi-degré. De même, le Soleil étant très loin, les tangentes T1 (extérieure) et T2 (intérieure) sont quasi-parallèles, donc le rayon d'une section normale au cône de pénombre au niveau de la Terre est très proche du diamètre de la Lune, donc le diamètre de la section normale du cône de pénombre au niveau de la Terre est de l'ordre de deux diamètres lunaires, soit environ 7000 km. Ainsi la pénombre ne recouvre jamais entièrement la surface terrestre, mais uniquement 16% d'un demi-hémisphère terrestre.
La taille du diamètre de la section normale au cône d'ombre au niveau de la Terre dépend des distances Terre-Lune et Soleil-Lune, on montre, à l'aide des valeurs extrêmes de ces distances que le diamètre de la section normale au cône d'ombre pour une éclipse totale est au maximum de 268 km et que le diamètre de la section normale au prolongement du cône d'ombre pour une éclipse annulaire est au maximum de 375 km. Bien évidemment l'ombre et le prolongement de l'ombre coupent la surface de la Terre suivant un ovale (intersection d'un cône et d'une sphère) dont le grand axe peut dépasser largement ces valeurs extrêmes, c'est le cas notamment pour les éclipses rasantes (proches des pôles).
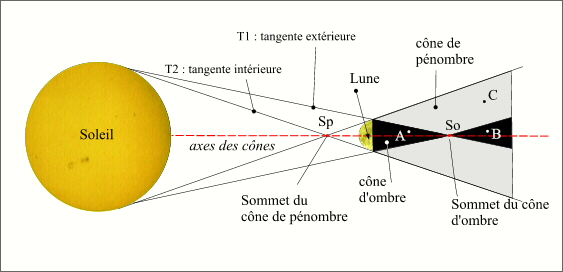
Différents types d'éclipses en fonction de la position de l'observateur.
Crédit : IMCCE/Patrick Rocher
Caractéristiques des cônes d'ombre et de pénombre-2
Les vitesses
La vitesse à laquelle se déplace l'ombre où le prolongement de l'ombre sur la surface de la Terre est la combinaison de deux mouvements : le mouvement de l'ombre dans l'espace qui est égal au mouvement de la Lune par rapport au Soleil vu depuis la Terre fixe et le mouvement de la surface terrestre du à la rotation de la Terre sur elle-même. Depuis la Terre, le Soleil et la Lune se déplacent par rapport aux étoiles d'ouest en est (mouvement direct), la Lune se déplace environ treize fois plus vite que le Soleil, son ombre se déplace d'environ 1 km/s par rapport à la Terre supposée fixe. La Terre tourne sur elle-même également d'ouest en est. La vitesse de l'ombre par rapport au sol est donc égale à la différence de la vitesse de l'ombre de la Lune et de la vitesse du sol. À l'équateur la vitesse du sol est de l'ordre de 500 m/s, la différence des deux vitesses est de 500m/s, plus on s'écarte en latitude de l'équateur, plus la vitesse de l'ombre est grande pour atteindre 1 km/s aux pôles (vitesse du sol nulle).
En savoir plus: Le calcul exact des vitesses : la vitesse de l'ombre à la surface terrestre
 En savoir plus
En savoir plus
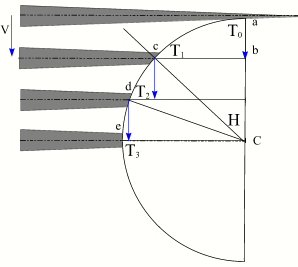
Vitesse de l'ombre à la surface d'une Terre fixe.
Crédit : IMCCE/Patrick Rocher
En réalité, le calcul de la vitesse de l'ombre à surface du sol est plus complexe, dans l'explication précédente nous avons fait des simplifications qui ne sont vraies que lorsque les vecteurs vitesses de l'ombre et du sol sont colinéaires. Dans un premier temps, on peut supposer une Terre fixe avec une ombre de la Lune se déplaçant avec une vitesse constante V par rapport à la Terre. Sur la figure ci-contre nous avons tracé la position du cône d'ombre et de son axe à des instants T0, T1, T2 et T3 séparés par un intervalle de temps dt constant. Durant le premier intervalle 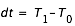 l'ombre de la Lune s'est déplacée de
l'ombre de la Lune s'est déplacée de 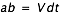 dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).
dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).
En savoir plus: Le calcul exact des vitesses : combinaison des vitesses
 En savoir plus
En savoir plus
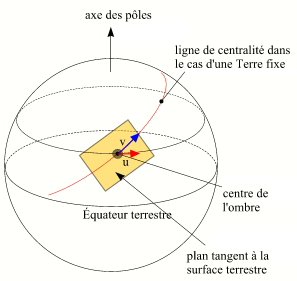
Combinaison des vitesses de l'ombre de la Lune et de la surface terrestre.
Crédit : IMCCE/Patrick Rocher
Pour avoir la vitesse, et la trajectoire, de l'ombre par rapport au sol dans le cas d'une Terre en rotation sur elle-même, il convient de combiner les deux mouvements. Si v est le vecteur vitesse de l'ombre (par rapport à la Terre fixe) dans le plan tangent au point de contact de l'axe du cône avec la surface terrestre et u le vecteur vitesse du sol dans le même plan, alors la vitesse de l'ombre par rapport au sol est égale à la différence des deux vecteurs vitesses (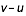 ). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.
). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.
En savoir plus: Le calcul des rayons de l'ombre et de la pénombre
 En savoir plus
En savoir plus
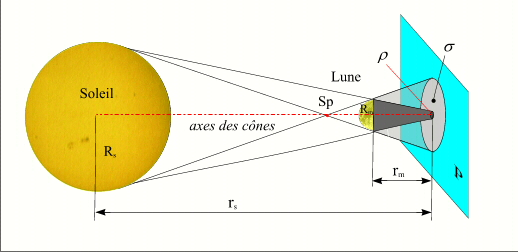
Éclipse totale : géométrie de l'ombre et de la pénombre dans un plan normal à l'axe des cônes.
Crédit : IMCCE/Patrick Rocher
Soit P un plan normal à l'axe des cônes d'ombre et de pénombre, ρ et σ les rayons des cercles définis par les intersections du cône de d'ombre et du cône de pénombre avec ce plan. Soit Rs le rayon solaire, Rm le rayon lunaire, rs et rm les distances respectives du centre du Soleil et du centre de la Lune au plan P. Une simple application du théorème de Thalès nous donne les valeurs de ρ et σ en fonction de Rs, Rm, rs et rm.
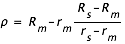
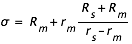
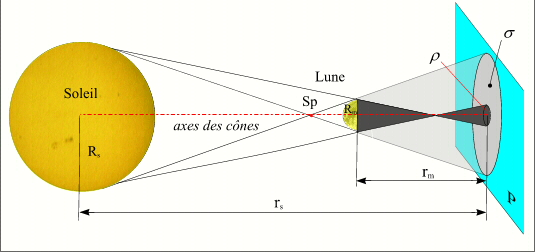
Éclipse annulaire : géométrie de l'ombre et de la pénombre dans un plan normal à l'axe des cônes.
Crédit : IMCCE/Patrick Rocher
Lorsque l'éclipse est annulaire le plan P coupe l'axe des cônes après le sommet du cône d'ombre, il coupe donc le prolongement du cône d'ombre. Les formules précédentes sont également applicables si l'on accepte que les rayons aient des valeurs négatives.
En savoir plus: Le calcul des rayons de l'ombre et de la pénombre-2
 En savoir plus
En savoir plus
Le tableau suivant donne les valeurs extrêmes de ρ et σ en fonction des distances Terre-Soleil et Terre-Lune. Dans le tableau on se place d'abord dans le plan du centre de la Terre, puis l'on se place à la surface de la Terre avec les deux corps au zénith, les distance Terre-Lune et Terre-Soleil sont alors diminuées d'un rayon terrestre, en fait, on néglige le rayon terrestre devant la distance Terre-Soleil. Dans ce tableau le rayon solaire est pris égal à Rs = 696 000 km, le rayon lunaire est pris égal à Rm = 1738,1 km et le rayon terrestre est pris égal à Re = 6400 km. Nous donnons également ρ et σ en secondes d'arcs, dans ce cas, ces valeurs représentent les rayons sélénocentriques (vu depuis le centre de la Lune) apparents des intersections des cônes d'ombre et de pénombre avec le plan P.
|
Périgée |
Moyenne |
Apogée |
| rm
|
357 200 km |
381 300 km |
407 000 km |
| rs
|
1,52 108 km |
1,50 108 km |
1,48 108 km |
|
ρ(km) |
104,9 km |
-34,7 km |
- 187,4 km
|
|
ρ(") |
60,5" |
-18,7 |
-94,8 km |
|
σ(km) |
3 379 km |
3 520 km |
3 673 km |
|
σ(") |
1948" |
1901" |
1859" |
| rm-Re
|
305 800 km |
374 900 km |
400 600 km |
|
ρ(km) |
134,1 km
|
-5.0 km |
-157 km |
|
ρ(") |
78,7" |
-2,8" |
-80,8" |
|
σ(km) |
3 350 km |
3 490 km |
3 643 km |
|
σ(") |
1966" |
1918" |
1873" |
Les valeurs extrêmes pour les éclipses périgées et apogées sont en italique et l'on retrouve bien les valeurs des diamètres de 268 km pour une éclipse périgée (donc totale) et de 375 km pour une éclipse apogée (donc annulaire). De même on constate que le diamètre de la pénombre qui est compris entre 6700 km et 7300 km est bien du même ordre de grandeur que deux diamètres lunaires.
Magnitude ou grandeur d'une éclipse de Soleil
Toutes les éclipses de Soleil ne sont pas identiques, il convient donc de trouver un paramètre qui les caractérise, ce paramètre est la grandeur ou la magnitude de l'éclipse, ces deux termes désignent la même quantité.
À un instant donné la grandeur g de l'éclipse est l'inverse du rapport du diamètre du Soleil sur la distance du bord du Soleil le plus rapproché du centre de la Lune au bord de la Lune le plus rapproché du centre du Soleil.
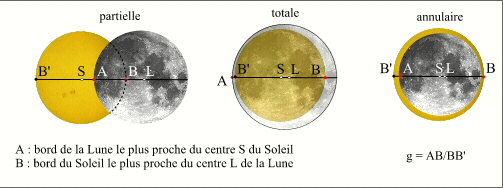
Grandeur ou magnitude d'une éclipses de Soleil.
Crédit : IMCCE/Patrick Rocher
Dans la figure ci-contre, nous avons ajouté une transparence à la Lune dans le cas de l'éclipse totale, cela permet de voir la position du Soleil. Comme on le constate sur la figure, les éclipses partielles et annulaires ont une grandeur inférieure à un et les éclipses totales ont une grandeur supérieure à un. Les éclipses mixtes ont une grandeur très proche de un. Pour les éclipses annulaires, plus la grandeur s'approche de un, plus le diamètre apparent de la Lune est proche du diamètre apparent du Soleil, donc plus l'éclipse est courte. Pour les éclipses totales, plus on s'écarte de un, plus le diamètre apparent de la Lune est grand par rapport au diamètre apparent du Soleil, donc plus l'éclipse est longue.
Degré d'obscuration d'une éclipse
Le degré d'obscuration est aussi un paramètre caractéristique des éclipses de Soleil. Le degré obscuration est le pourcentage de la surface du disque solaire occulté par la Lune.
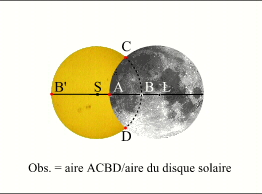
Le degré d'obscuration.
Crédit : IMCCE/Patrick Rocher
Le degré d'obscuration donne une information pour les éclipses annulaires et partielles car sa valeur est inférieure à 100%, par contre toutes les éclipses totales ont un degré d'obscuration de 100% quelle que soit la grandeur de l'éclipse.
La grandeur et le degré d'obscuration sont donnés dans les circonstances générales des éclipses, ce sont alors les valeurs maximales de ces paramètres sur toute la durée de l'éclipse, elles correspondent à un instant et un lieu bien défini sur la Terre : le lieu du maximum de l'éclipse (lieu sur la Terre où la grandeur est maximale) et l'instant où la grandeur est maximale en ce lieu. Ces deux valeurs sont également données dans les circonstances locales des éclipses, dans ce cas elles sont toujours inférieures ou égales (si on est au lieu du maximum) à celles données dans les circonstances générales.
Détermination des types d'éclipses en fonction des positions orbitales
Introduction
 Introduction
Introduction
Après avoir traité de l'aspect purement géométrique des éclipses (tailles et vitesses des cônes d'ombre et de pénombre) dans les sections précédentes, nous avons commencer à faire intervenir les aspects liés aux positions des trois corps. Nous allons dans cette section répondre partiellement à la question, où se trouvent la Lune et le Soleil sur leurs orbites pour qu'une éclipse soit totale, annulaire ou mixte. Dans un premier temps nous raisonnerons sur les diamètres apparents, puis nous verrons une autre approche à partir des distances à la Terre.
Diamètres apparents
En raison des mouvements orbitaux de la Terre et de la Lune, les distances Terre-Lune et Soleil-Terre ne sont pas constantes, les diamètres apparents de la Lune et du Soleil sont donc variables. Le diamètre apparent de la Lune est maximal lorsque la Lune est proche de la Terre donc à son périgée, et il est minimal lorsque la Lune est loin de la Terre donc à son apogée. De même le diamètre apparent du Soleil est maximal lorsqu'il est proche de la Terre donc lorsque le Soleil apparent est à son périgée ou la Terre est à son périhélie (actuellement vers le 4 janvier) et le diamètre apparent du Soleil est minimal lorsque le Soleil est loin de la Terre, donc lorsque le Soleil apparent est à l'apogée ou la Terre à l'aphélie (actuellement vers le 4 juillet).
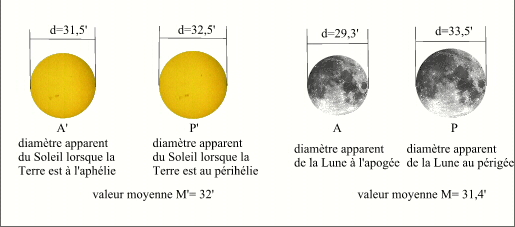
Valeurs extrêmes et moyennes des diamètres apparents du Soleil et de la Lune.
Crédit : IMCCE/Patrick Rocher
Comme on le constate sur la figure ci-contre le diamètre apparent moyen de la Lune est plus petit que le diamètre apparent moyen du Soleil, on peut donc s'attendre à avoir en moyenne plus d'éclipses annulaires que d'éclipses totales.
Positions orbitales
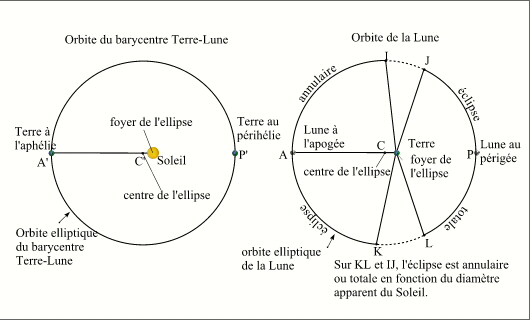
Analyse des types d'éclipses solaire en fonction des positions orbitales de la Terre et de la Lune.
Crédit : IMCCE/Patrick Rocher
Comme nous venons de le voir, nous pouvons calculer les valeurs extrêmes des diamètres apparents de la Lune et du Soleil vus depuis la Terre. Nous allons affiner un peu notre étude, en effet nous pouvons déterminer la portion de l'orbite lunaire sur laquelle le diamètre apparent de la Lune est toujours plus grand que le plus grand diamètre apparent du Soleil (32,5'), c'est l'arc d'orbite LJ sur la figure ci-contre. Sur cette portion d'orbite lunaire les éclipses centrales sont toujours totales, quelle que soit la position de la Terre sur son orbite. Nous pouvons également déterminer la portion de l'orbite lunaire sur laquelle la Lune a un diamètre apparent toujours plus petit que le plus petit diamètre apparent du Soleil (31,5'), c'est l'arc d'orbite IK sur la figure ci-contre. Sur cette portion d'orbite les éclipses centrales sont toujours annulaires quelle que soit la position de la Terre sur son orbite. Sur les portions d'orbites IJ et KL le diamètre apparent de la Lune varie entre 31,5' et 32,5' (valeurs extrêmes du diamètre apparent du Soleil) le type de l'éclipse centrale est donc déterminé par le diamètre apparent du Soleil donc par la position de la Terre sur son orbite. C'est sur ces portions de l'orbite de la Lune que l'on trouve les éclipses mixtes.
On remarquera que sur la figure ci-contre, les orbites de la Terre et de la Lune sont représentées par des cercles, cela est totalement justifié compte tenu des faibles excentricités des orbites lunaire et terrestre. Par contre les corps centraux ne sont pas aux centres des cercles mais sont excentrés. On notera également que l'arc LJ est centré sur le périgée de la Lune, donc les éclipses avec la Lune au périgée sont toujours des éclipses totales, de même l'arc IK est centré sur l'apogée de la Lune donc les éclipses avec la Lune en apogée sont toujours des éclipses annulaires. Enfin l'arc IK est plus grand que l'arc LJ, cela confirme le fait qu'il y ait en moyenne plus d'éclipses annulaires que d'éclipses totales.
Types d'éclipses en fonction des distances des corps
Nous pouvons avoir une autre approche du problème en considérant les distances Soleil-Lune et Lune-Terre, en effet il y a équivalence entre les diamètres apparents et les distances des corps entre eux.
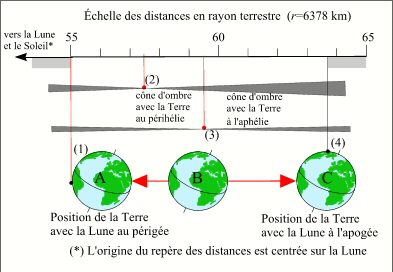
Positions extrêmes pour les éclipses centrales de Soleil.
Crédit : IMCCE/Patrick Rocher
- (1) est la distance observateur-Lune minimale, d=55,0 rayons terrestres, c'est-à-dire avec la Lune au périgée et l'observateur avec la Lune au zénith,
- (4) est la distance observateur-Lune maximale, d=63,8 rayons terrestres, c'est-à-dire avec la Lune à l'apogée et l'observateur avec la Lune à l'horizon,
- (2) correspond à une distance Lune sommet du cône d'ombre de longueur minimale, l=57,5 rayons terrestres, c'est à dire une distance Soleil-Terre minimale donc un Soleil au périgée (ou la Terre au périhélie),
- (3) correspond à une distance Lune sommet du cône d'ombre de longueur maximale, l=59,5 rayons terrestres, c'est-à-dire une distance Soleil-Terre maximale donc un Soleil à l'apogée (ou la Terre à l'aphélie).
Types d'éclipses en fonction des distances des corps-2

Positions extrêmes pour les éclipses centrales de Soleil.
Crédit : IMCCE/Patrick Rocher
Cette figure donne les distances extrêmes de la Terre et du cône d'ombre, en fonction des positions extrêmes de la Lune, du Soleil et de la Terre. L'origine des distances est le centre de la Lune et les distances sont exprimées en rayons terrestres. La distance observateur-Lune varie de 55 à 63,8 rayons terrestres. La distance entre la Lune et le sommet du cône d'ombre varie, elle, de 57 à 59,5 rayons terrestres. Cette figure nous montre que si, au moment de l'éclipse, on est dans la position A, c'est-à-dire avec la Lune au périgée, alors quelle que soit la position de la Terre sur son orbite, l'éclipse est totale car la Terre coupe toujours le cône d'ombre avant son sommet. De même si, au moment de l'éclipse, on est en position C, c'est-à-dire avec la Lune à son apogée, alors quelle que soit la position de la Terre sur son orbite l'éclipse est annulaire car la Terre coupe toujours le prolongement de l'ombre. En faisant varier la position de la Terre (par rapport à la Lune) entre ces deux positions, on peut visualiser tous les cas intermédiaires possibles. Par exemple, lorsque la Terre est en B (distance Lune-Terre = 59 r), si la Terre est au périhélie (cône d'ombre en position 2) l'éclipse est annulaire car la Terre coupe le prolongement du cône d'ombre, si la Terre est à son l'aphélie (cône d'ombre en position 3) alors l'éclipse est totale car la Terre coupe le cône d'ombre, avec un cône d'ombre entre les positions 2 et 3 toutes les configurations sont possibles (éclipses totales, annulaires ou mixtes).
Circonstances générales et cartes des éclipses
Introduction
 Introduction
Introduction
Dans cette section, nous allons décrire les circonstances générales d'une éclipse de Soleil. Ces circonstances représentent l'évolution des contacts et des trajectoires des cônes d'ombres et de pénombres avec la surfaces terrestre. Ces circonstances générales décrivent donc l'évolution de l'éclipse vue par un observateur situé dans l'espace à l'extérieure de la surface terrestre. Nous présenterons ensuite les différentes cartes d'éclipses et les différentes projections qui y sont associées.
Circonstances générales
Les circonstances générales d'une éclipse correspondent aux différentes phases de l'éclipse générale ; ces phases sont les suivantes :
- le commencement et la fin de l'éclipse générale, ce sont les deux instants et les deux lieux sur Terre où le cône de pénombre de la Lune est tangent extérieur à la surface de l'ellipsoïde terrestre,
- le commencement et la fin de l'éclipse totale ou annulaire, ce sont les deux instants et les deux lieux sur Terre où le cône d'ombre de la Lune est tangent extérieur à la surface de l'ellipsoïde terrestre,
- le commencement et la fin de la centralité, ce sont les deux instants et les deux lieux sur Terre où l'axe du cône d'ombre de la Lune est tangent à la surface de l'ellipsoïde terrestre,
- le maximum de l'éclipse, c'est l'instant et le lieu sur Terre où la grandeur de l'éclipse est maximale,
- et l'éclipse centrale à midi ou minuit vrai, c'est l'instant et le lieu sur Terre où le maximum de l'éclipse se produit lorsque le Soleil est dans le plan du méridien. L'éclipse peut effectivement être centrale à minuit vrai, cela arrive lorsque l'éclipse est proche des pôles terrestres, le Soleil passe alors deux fois au méridien par jour à midi vrai et à minuit vrai.
Comme on le constate, ces différentes phases sont liées à l'évolution de l'ombre et de la pénombre à la surface de la Terre, les débuts et fins de chaque phase correspondent à un instant bien particulier et à un lieu unique à la surface du globe terrestre. La différence de temps entre le début et la fin de l'éclipse générale nous donne le temps mis par la pénombre pour parcourir la surface terrestre. De même la différence de temps entre le début et la fin de la phase totale ou annulaire, lorsqu'elles existent, donne le temps mis par l'ombre ou son prolongement pour parcourir la surface terrestre.
En savoir plus: Circonstances générales de l'éclipse des 10 et 11 juin 2002
 En savoir plus
En savoir plus
| Circonstance |
UT |
Longitude |
Latitude |
| Commencement de l'éclipse générale |
le 10 à 20h 51,8m |
-137° 58,5' |
-2° 30,0' |
| Commencement de l'éclipse annulaire |
le 10 à 21h 53,9m |
-120° 51,74 |
+1° 16,0' |
| Commencement de l'éclipse centrale |
le 10 à 21h 54,5m |
-120° 40,8' |
+1° 19,5' |
| Maximum de l'éclipse |
le 10 à 23h 44,3m |
+178° 36,8' |
+34° 32,7' |
| Éclipse centrale à midi ou minuit vrai |
le 10 à 23h 48,2m |
+177° 11,4' |
+34° 55,3' |
| Fin de l'éclipse centrale |
le 11 à 1h 34,0m |
+104° 49,2' |
+19° 48,1' |
| Fin de l'éclipse annulaire |
le 11 à 1h 34,6m |
+104° 59,4' |
+19° 44,9' |
| Fin de l'éclipse générale |
le 11 à 2h 36,6m |
+122° 15,8' |
+16° 1,0' |
Dans ce tableau les longitudes sont comptées positivement vers l'ouest et négativement vers l'est. On remarquera que l'éclipse se déplace d'ouest en est et du sud vers le nord. On donne toujours les instants des différentes phases des éclipses en Temps universel coordonné, cela évite les problèmes liés aux heures locales. Dans notre exemple, l'éclipse est à cheval sur deux jours en temps universel coordonné, le 10 et le 11 juin 2002.
La phase annulaire débute le 10 juin à 21h 53,9m UTC en un point de longitude -120° 51,7' (est) et de latitude 1° 16,0' (nord), ce lieu se trouve à l'est en Indonésie (au nord des Célèbes), la phase annulaire se termine le 11 juin à 1h 34,6m UTC en un point de longitude +104° 59,4' (ouest) et de latitude +19° 44,9' (nord), ce lieu se trouve sur la côte ouest du Mexique. Si l'on exprime ces instants en heures locales, le début de la phase annulaire, en Indonésie est le 10 juin à 21h 53,9m + 8h = 29h 53,9m soit le 11 juin à 5h 53,9m temps légal en Indonésie, donc le 11 juin 2002 au matin, et la fin de la phase annulaire, au Mexique est le 11 juin à 1h 34,6m - 7h = -5h 25,4m = 18h 34,6m le 10 juin en temps légal au Mexique, donc le 10 juin 2002 au soir. On a donc la phase annulaire qui commence le matin du 11 juin 2002 en Indonésie et se termine le soir du 10 juin au Mexique, elle se termine donc en temps légal avant d'avoir commencé, ce qui est normal car la bande de centralité traverse la ligne de changement de date d'ouest en est donc on perd un jour en temps légal.
L'usage systématique du Temps universel évite ces paradoxes temporels pour les éclipses franchissant la ligne de changement de date, néanmoins l'observateur, lors de ses déplacements doit tenir compte des passages en heures légales s'il ne veut pas arriver un jour trop tard pour son observation !
Les cartes d'éclipses
On distingue deux types de cartes, les cartes générales et les cartes locales.
Pour chaque éclipse, on trace généralement une ou deux cartes générales de l'éclipse. Sur ces cartes on fait figurer les courbes suivantes : la bande de centralité (lorsqu'elle existe), les limites boréale et australe de l'éclipse, les courbes de commencement, de fin et de maximum au lever et au coucher du Soleil, ainsi que les courbes de commencement et fin pour des instants donnés (toutes les heures en général). Pour le tracé de ces cartes, on utilise une projection stéréographique, c'est-à-dire une projection azimutale conforme. Cette projection, qui conserve les angles mais pas les distances, déforme les continents mais permet d'avoir une représentation des pôles terrestres sur la carte. On utilise également une projection orthographique, elle permet de représenter la trajectoire de l'éclipse sur un globe terrestre vu de l'espace.
On trace également, un certain nombre de cartes locales. Sur ces cartes, on donne également les courbes de commencement, de fin et de maximum pour des instants donnés (avec un pas plus adapté à la carte), et parfois on trace aussi la projection de l'ombre pour des instants donnés. Les cartes locales sont tracées à l'aide de différentes projections en fonction des lieux représentés (projection conforme de Lambert, projection de Mercator...).
En savoir plus: Exemple de carte générale en projection stéréographique
 En savoir plus
En savoir plus
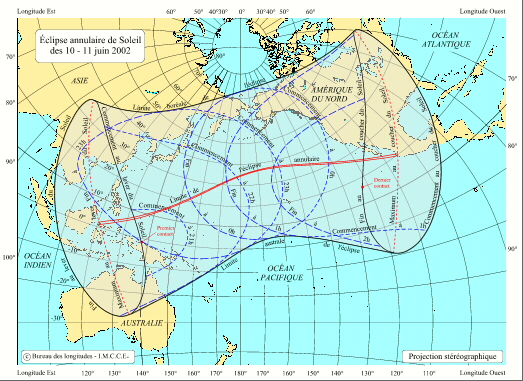
Carte générale de l'éclipse des 10 - 11 juin 2002
Crédit : IMCCE/Patrick Rocher
Sur cette carte on a tracé la bande de centralité (en rouge), les limites boréale et australe de l'éclipse, ce sont les limites boréale et australe du cône de pénombre durant l'éclipse. On donne également les limites du cône de pénombre toutes les heures (commencement et fin à un instant donné, courbes bleues) et les lieux des commencements, maxima et fins d'éclipse au lever et au coucher du Soleil (courbes noires et rouges joignant les extrémités des limites boréale et australe de l'éclipse). On notera la différence de taille entre la surface terrestre où l'éclipse est visible sous la forme d'une éclipse partielle (surface grisée) et la surface de la bande de centralité.
Des cartes plus grandes, et plus lisibles, sont disponibles sur le serveur de l'IMCCE.
En savoir plus: Exemple de carte en projection orthographique
 En savoir plus
En savoir plus
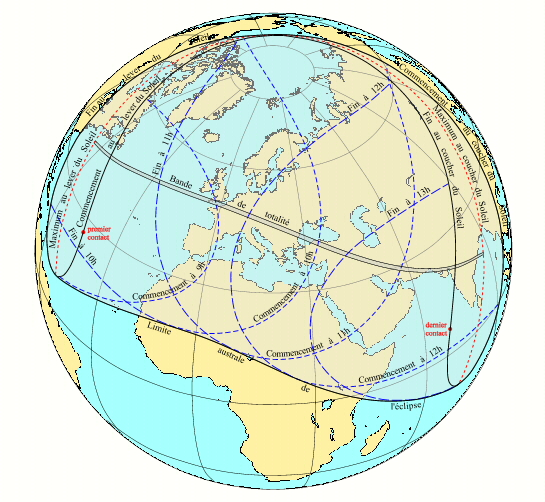
Projection orthographique de l'éclipse du 11 août 1999.
Crédit : IMCCE/Patrick Rocher
La projection orthographique permet de représenter l'éclipse générale sur la Terre, vue depuis l'espace. Les courbes représentées sont les mêmes que dans la représentation stéréographique.
En savoir plus: Exemple de carte locale
 En savoir plus
En savoir plus
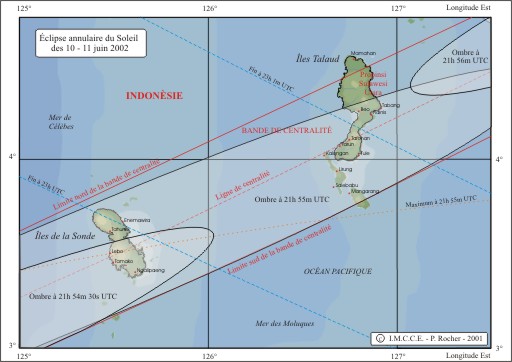
Carte locale de l'éclipse des 10 - 11 juin 2002 sur l'Indonésie.
Crédit : IMCCE/Patrick Rocher
Cette carte locale en projection de Lambert donne le tracé de la ligne de centralité sur une partie de l'Indonésie, les deux îles de cette carte sont les deux seuls lieux terrestres où la phase annulaire de l'éclipse fut observable. On a également tracé l'intersection du prolongement du cône d'ombre avec la surface terrestre. Comme on est en début d'éclipse, on notera l'aspect très allongé de la projection.
En savoir plus: Les différentes projections
 En savoir plus
En savoir plus
On peut classer les projections géographiques en fonction des propriétés géométriques des projections des parallèles et des méridiens d'une sphère. On entend par méridiens les grands cercles passant par le pôle de projections et par parallèles les cercles intersections de la sphère et des plans normaux à la direction des pôles.
Une projection est dite :
- méricylindrique si et seulement si le méridien central est une droite (ou un segment), si les parallèles sont des droites (ou des segments, éventuellement des points) perpendiculaires au méridien central, et si les méridiens des courbes coupent les parallèles à intervalles réguliers.
- cylindrique si et seulement si elle est méricylindrique et si les méridiens sont des droites parallèles entre elles.
- polyconique si et seulement si le méridien central est une droite, si les parallèles sont des arcs de cercles dont les centres sont sur le méridien central et si les méridiens des courbes coupent les parallèles à intervalles réguliers.
- mériconique si et seulement si elle est polyconique et si les parallèles sont concentriques.
- tronconique si et seulement si elle est mériconique et si les méridiens sont des droites qui se coupent au centre des parallèles.
- conique si et seulement si elle est tronconique et si un des pôle est ponctuel (par pôle on entend un point de latitude +/-90°).
- azimutale (ou zénithale) si et seulement si elle est conique et si les parallèles sont des cercles complets.
Une projection à partir d'un centre de projection sur une surface quelconque, suivie d'un développement de cette surface s'appelle une projection perspective. par exemple les projections cylindriques et coniques sont des projections perspectives.
Les projections sont également classées en fonction des propriétés qu'elles conservent. On distingue donc de projections :
- Équivalentes
: lorsque qu'il y a conservation des aires.
- Conformes : lorsqu'il y a conservation locale des angles, donc les formes.
- Équidistantes : lorsqu'il y a conservation des distances sur les méridiens.
- Équidistantes : lorsqu'il y a conservation les distances sur les méridiens (la conservation de toutes les distances n'étant pas possible).
- Orthodromiques : lorsqu'un un grand cercle de la sphère est représenté par une droite, alors le plus court chemin entre deux points est un segment de droite sur la carte. Ceci est utile en navigation (beaucoup de cartes marines utilisent cette projection).
- Loxodromiques : lorsque les courbes d'azimut constant sont des droites (ou des segments de droite). Cette propriété découle directement de la conformité et du fait que les méridiens sont des droites parallèles.
- Transverse : lorsque l'on intervertit le rôle des latitudes et des longitudes.
Les autres projections sont dites aphylactiques.
Quelques exemples :
- La projection de Mercator est une projection cylindrique conforme et elle est loxodromique.
- La projection stéréographique, appelée également projection gnomonique, est une projection azimutale conforme, elle est orthodromique.
- La projection orthogonale, appelée également projection orthographique, est une projection azimutale conforme.
Circonstances locales des éclipses
Introduction
 Introduction
Introduction
Dans cette section nous allons décrire les circonstances locales d'une éclipse. C'est-à-dire ce que voit un observateur à la surface de la Terre. Dans ce cas on regarde le Soleil et la Lune (et non la Terre et l'ombre de la Lune). L'observateur en fonction de sa position, verra ou ne verra pas d'éclipses. Dans le cas d'une éclipse centrale, suivant sa position, il verra la phase centrale ou non.
La partie pour en savoir plus est complexe et demande une bonne connaissance du calcul numérique.
Circonstances locales éclipses totales
Il ne faut pas les confondre avec les circonstances générales décrites dans le paragraphe précédent. Les circonstances locales d'une éclipse décrivent, en un lieu donné, les différentes phases de l'éclipse, observables par un observateur situé en ce lieu.
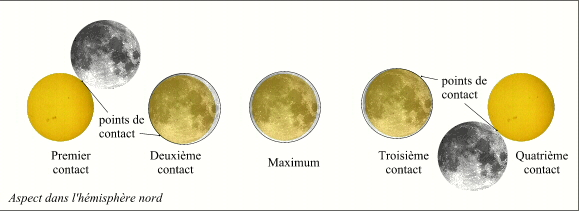
Phases locales d'une éclipse totale.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre nous montre les différentes phases observables par un observateur situé dans la bande de totalité durant une éclipse totale de Soleil, pour rendre le dessin plus lisible nous avons ajouté une transparence à la Lune durant la totalité pour permettre de voir la position du Soleil occulté par la Lune. La durée de la phase de totalité en ce lieu est égale à l'intervalle de temps séparant les second et troisième contacts. La durée de l'éclipse locale (phases partielles et phase totale) est égale à l'intervalle de temps séparant les premier et quatrième contacts. Les points de Baily apparaissent au voisinage des deuxième et troisième points de contacts.
Circonstances locales éclipses annulaires
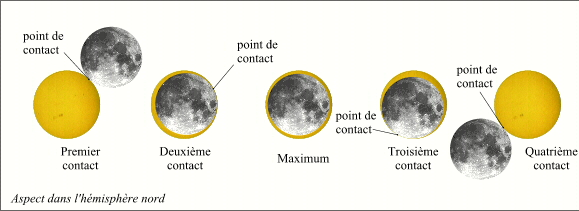
Phases locales d'une éclipse annulaire.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre nous montre les différentes phases observables par un observateur situé dans la bande de centralité d'une éclipse annulaire. La durée de la phase annulaire en ce lieu est égale à l'intervalle de temps séparant les second et troisième contacts. La durée de l'éclipse locale (phases partielles et phase annulaire) est égale à l'intervalle de temps séparant les premier et quatrième contacts.
Circonstances locales éclipses partielles

Phases locales d'une éclipse partielle.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre nous montre les différentes phases observables par un observateur situé sur le trajet du cône de pénombre d'une éclipse. L'éclipse peut être partielle, annulaire ou totale. Dans les deux derniers cas, l'observateur n'est pas dans la bande de centralité, il observe donc l'éclipse annulaire ou totale sous la forme d'une éclipse partielle. La durée de l'éclipse locale (phase partielle) est égale à l'intervalle de temps séparant les premier et quatrième contacts.
Ces phases sont les suivantes :
- le début de l'éclipse partielle, appelé également premier contact (parfois premier contact extérieur),
- le début de l'éclipse totale ou annulaire (si l'observateur est dans la bande de centralité), appelé également deuxième contact (parfois premier contact intérieur),
- le maximum de l'éclipse, instant où la grandeur est maximum en ce lieu,
- la fin de l'éclipse totale ou annulaire (si l'observateur est dans la ligne de centralité), appelée également troisième contact (parfois deuxième contact intérieur),
- la fin de l'éclipse partielle, appelée également quatrième contact (parfois deuxième contact extérieur).
Circonstances locales angles au pole et au zenith
Pour chacun des contacts, en plus des instants du contact, on donne à l'observateur l'angle au pôle
P et l'angle au zénith Z. On remarquera que les points des contacts intérieurs des éclipses totales sont diamétralement opposés aux points des contacts intérieurs des éclipses annulaires.
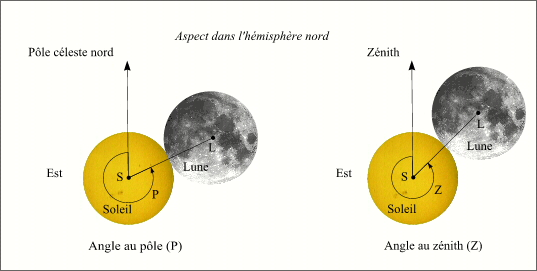
Définitions des angles au pôle et au zénith
Crédit : IMCCE/Patrick Rocher
L'angle au pôle P d'un contact est l'angle de la direction nord N (partie boréale du cercle horaire du centre S du Soleil) avec l'arc de grand cercle joignant les centres S et L du Soleil et de la Lune, compté positivement vers l'est, dans le sens nord-est-sud-ouest.
L'angle au zénith Z d'un contact a une définition analogue à celle de P, en remplaçant le cercle horaire du centre S du Soleil par le vertical du même point.
Circonstances locales-5
 Remarques
Remarques
Sous nos latitudes (en France) et pour les latitudes positives situées au-dessus du tropique du Cancer (latitudes supérieures à 23°), le Soleil passe au méridien au sud, donc quand on regarde le Soleil, l'ouest est à droite du Soleil et l'est est à sa gauche. La Lune éclipse le Soleil d'ouest en est (donc de la droite vers la gauche lorsque l'on regarde le Soleil). Pour les latitudes négatives situées sous le tropique du Capricorne (latitudes inférieures à -23°), le Soleil passe au méridien au nord, l'aspect du phénomène est inversé, l'éclipse a, bien évidemment, toujours lieu d'ouest en est, mais elle a lieu de la gauche vers la droite car on regarde le Soleil vers le nord. Dans la zone intertropicale les deux cas de figure sont possibles, cela dépend de la date de l'éxclipse et du lieu d'observation. La connaissance des instants et positions du deuxième et du troisième point de contact est très importante pour les éclipses totales de Soleil, car elle indique quand et où vont apparaître les points de Baily.
Avec l'instant du maximum on donne également la grandeur de l'éclipse, le degré d'obscuration, la hauteur h et l'azimut a du Soleil.
La hauteur h du Soleil sur l'horizon est l'angle de la direction du Soleil et du plan horizontal, compté en degrés de -90° à +90°.
L'azimut est l'angle formé par la projection de la direction du Soleil dans le plan horizontal avec la direction du Sud, compté en degré dans le sens rétrograde (sud = 0°, ouest = 90°, nord = 180°, est = 270°).
Les circonstances locales d'une éclipse peuvent être calculées à l'aide des éléments de Bessel
En savoir plus: Définition des éléments de Bessel
 En savoir plus
En savoir plus
Au XIXe siècle, l'astronome allemand Friedrich Bessel (1784-1846) a mis au point une méthode, toujours utilisée de nos jours, pour faciliter le calcul des circonstances locales et générales d'une éclipse de Soleil.
Pour un lieu donné il y a lieu de déterminer :
- les instants des différents contacts,
- l'instant du maximum de l'éclipse et la grandeur de l'éclipse à cet instant,
- les angles au pôle et au zénith de chacun des contacts.
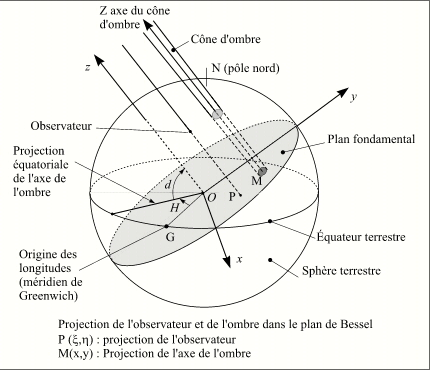
Les éléments de Bessel.
Crédit : IMCCE/Patrick Rocher
Le lieu d'observation est défini par sa longitude λ (positive à l'ouest et négative à l'est du méridien de Greenwich), sa latitude ϕ et son altitude h au-dessus du niveau de la mer.
On définit à chaque instant un système de coordonnées Oxyz de sens direct, dans lequel :
O est le centre de la Terre.
L'axe Oz est parallèle à l'axe des cônes de pénombre et d'ombre, le sens positif étant celui qui va de la Terre à la Lune.
L'axe Ox est l'intersection du plan fondamental Oxy perpendiculaire à Oz et du plan de l'équateur terrestre, le sens positif étant vers l'est.
L'axe Oy est normal à Ox dans le plan fondamental, le sens positif étant vers le nord.
En savoir plus: Définition des éléments de Bessel-2
 En savoir plus
En savoir plus
En utilisant comme unité de longueur le rayon équatorial terrestre, les éléments de Bessel sont définis de la manière suivante :
x, y, z sont les coordonnées du centre de la Lune.
d et H sont la déclinaison de l'axe Oz et son angle horaire par rapport au méridien de Greenwich.
fe et fi sont les demi-angles au sommet des cônes de pénombre et d'ombre, fe étant pris par convention positif et fi négatif.
ue et ui sont les rayons des sections circulaires des cônes de pénombre et d'ombre par le plan fondamental Oxy et s'obtiennent par les formules suivantes :
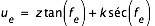
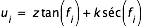
où k est le rayon de la Lune exprimé en rayon équatorial terrestre.
En savoir plus: Définition des éléments de Bessel-3
 En savoir plus
En savoir plus
Les coordonnées ξ, η, ζ du lieu d'observation dans le système Oxyz sont :
ξ = ρ . cos ϕ ' . sin (H - λ ),
η = ρ . sin ϕ ' . cos d - ρ . cos ϕ ' . sin d . cos ( H - λ ),
ζ = ρ . sin ϕ ' . sin d + ρ . cos ϕ ' . cos d . cos ( H - λ ),
avec :
ρ . cos ϕ ' = cos u + h/r0 . cos ϕ
ρ . sin ϕ ' = (1 - f) . sin u + h/r0 . sin ϕ
et
tan u = (1 - f) . tan ϕ
où h est l'altitude du lieu exprimée en mètres, r0 est le rayon équatorial terrestre exprimé en mètres et f l'aplatissement de l'ellipsoïde terrestre (f = 1/298,257 = 0,003 35281).
En savoir plus: Définition des éléments de Bessel-4
 En savoir plus
En savoir plus
Les variations horaires ξ ', η ', ζ ' de ces coordonnées sont fournies avec une précision de l'ordre de la seconde de temps par les formules suivantes, H' étant exprimé en radians par heure.
ξ ' = H' . ρ . cos ϕ ' . cos (H - λ ),
η ' = H' . ξ . sin d,
ζ ' = - H' . ξ . cos d,
Les rayons le et li des sections circulaires des cônes de pénombre et d'ombre par le plan mené par le lieu d'observation parallèlement au plan fondamental s'obtiennent par les formules suivantes :
le =ue - ζ tan fe
li = ui - ζ tan fi
En savoir plus: Calcul des circonstances locales
 En savoir plus
En savoir plus
Chaque élément de Bessel que l'on pourra désigner par b est représenté sur un intervalle de temps (t0, t1) par des coefficients de développements en polynômes du temps, à l'exception de tan fe et de tan fi qui sont considérées comme constantes sur l'intervalle. Un élément de Bessel se calcule à un instant t par la formule :
b = b0 + b1 . T + b2 . T2 + b3 . T3
avec T = t - t0.
T, exprimé en heure, représente le temps écoulé depuis l'instant origine t0.
La variation horaire b' d'un élément de Bessel se calcule par la formule :
b' = b1 + 2 b2 . T + 3 b3. T2
En savoir plus: Calcul de la grandeur maximale en un lieu
 En savoir plus
En savoir plus
Soient :
U = x - ξ , U' = x' - ξ',
V = y - η , V' = y' - η ',
On prend comme valeur de départ td l'époque du maximum de l'éclipse, l'instant du maximum tm se calcule en ajoutant à td la valeur Dtm donnée par :
Dtm = - (UU' + VV') / (U'2+ V'2)
On doit réitérer le calcul en prenant comme nouvelle valeur de départ la valeur de tm.
La grandeur maximale est donnée par :
g = (le - lm) / (le - li)
pour une éclipse annulaire ou totale au lieu considéré, où :
g = (le - lm) / (2 le- 0,5465) pour une éclipse partielle, avec :
lm = (U2 + V2)1/2
En savoir plus: Calcul des instants des contacts en un lieu
 En savoir plus
En savoir plus
On prend comme valeurs de départ td du premier et du quatrième contacts (contacts extérieurs) des valeurs approchées déduites de la carte de l'éclipse et l'on prend comme valeurs de départ du second et du troisième contacts (contacts intérieurs), lorsqu'ils existent, la valeur tm du maximum calculée précédemment.
Pour chaque valeur td de départ on calcule les quantités suivantes :
β = (UU' + VV') / (U'2 + V'2),
γ = (U2 + V2 - l2) / (U'2 + V'2),
θ = ±(β2 - γ)1/2
avec l = le ou l = li et θ étant du signe de β.
Les instants du premier et du quatrième contacts se calculent par la formule :
t = td - β + θ
et les instants du second et du troisième contacts se calculent par les formules :
t = td - β - |θ| pour le second contact,
et
t = td - β + |θ| pour le troisième contact.
Comme pour le calcul du maximum on doit réitérer les calculs en prenant comme nouvelles valeurs de départ les valeurs t.
En savoir plus: Calcul de l'angle au pôle et de l'angle au zénith
 En savoir plus
En savoir plus
La valeur de l'angle au pôle P d'un point de contact est donnée par :
tan P = U/V ,
où sin P a le signe de U, sauf pour les second et troisième contacts (contacts intérieurs) d'une éclipse totale pour lesquels sin P est de signe contraire à U.
L'angle au zénith Z d'un point de contact est donné par :
Z = P - Γ ,
en désignant par Γ l'angle parallactique défini d'une façon approchée par :
tan Γ = ξ/η ,
sin Γ étant du signe de ξ.
Réponses aux QCM
pages_types-eclipses/stlp-qcm-type-eclipse.html
QCM
'QCM sur les différents types d'éclipses'
- Question 1
Solution : réponse 1)
(
Les éclipses centrales annulaires, les éclipses centrales totales et les éclipses centrales annulaire-totales.
)
- Question 2
Solution : réponse 1)
- Question 3
Solution : réponse 2)
- Question 4
Solution : réponse 1)
- Question 5
Solution : réponse 2)
 Prérequis
Prérequis Introduction
Introduction















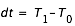 l'ombre de la Lune s'est déplacée de
l'ombre de la Lune s'est déplacée de 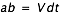 dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).
dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).

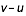 ). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.
). Ces deux vitesses ne sont pas colinéaires en raison de l'inclinaison de l'orbite lunaire sur l'équateur terrestre. La trajectoire de l'ombre sur le sol, donc sur une carte, est la combinaison des deux mouvements et n'est donc plus un petit cercle de la sphère terrestre. En réalité la Terre n'est pas une sphère mais un ellipsoïde de révolution. Cela complique encore un peu les calculs.