Diagramme HR et amas
A priori, rien ne ressemble plus aux étoiles d'un amas que les étoiles d'un autre amas. Si les étoiles d'un amas paraissent moins lumineuses que celles d'un deuxième, cette différence est largement due à sa distances plus importante par rapport à la Terre.
Cette propriété statistique peut donc être mise à profit pour comparer les distances desdits amas.
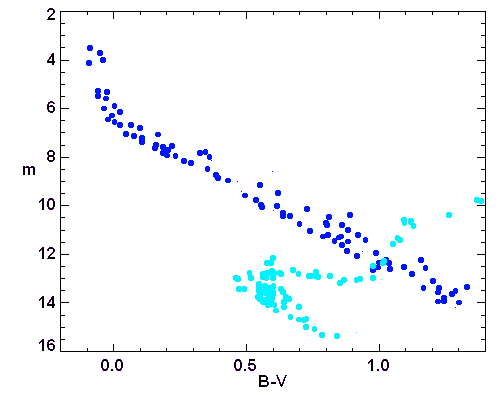
Superposition, dans un même diagramme HR (indice de couleur, magnitude visible apparente) des étoiles de l'amas M67 (bleu ciel), ou des Pléiades (bleu foncé). L'un est jeune (Pléiades), l'autre plus âgé ; les magnitudes apparentes dépendent de la distance.
Crédit :
ASM
 Objectifs
Objectifs
La mesure de la magnitude apparente et l'identification de la magnitude absolue d'un objet permettent de mesurer sa distance.
La température effective d'une étoile
Si l'on est capable de déterminer précisément la température effective d'une étoile, à partir de sa couleur ou de son type spectral, et que l'on peut lui affecter une classe de luminosité, le diagramme de Hertzsprung-Russell donne alors un moyen de déterminer sa distance.
Pour une supergéante bleue comme Rigel (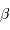 Orion), de type spectral B8 et de classe de luminosité Ia, avec une température de surface de 11500 K, on trouvera par exemple une magnitude absolue de
Orion), de type spectral B8 et de classe de luminosité Ia, avec une température de surface de 11500 K, on trouvera par exemple une magnitude absolue de 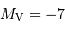 , ce qui, confronté à la mesure de sa magnitude apparente de 0.14, lui confère une distance de 268 pc.
, ce qui, confronté à la mesure de sa magnitude apparente de 0.14, lui confère une distance de 268 pc.
 Définition
Définition
On appelle parallaxe spectroscopique ce type de mesure de distance, qui s'obtient par comparaison de la magnitude apparente d'un objet, mesurée, à la magnitude absolue, induite indépendamment.
Diagramme HR et amas
Une autre façon de mesurer des distances à partir du diagramme H-R est d'utiliser des diagrammes couleur-magnitude d'amas d'étoiles, tout comme l'avait fait Hertzsprung au moment de sa découverte.
Les étoiles d'un amas étant toutes à la même distance, on peut tracer le diagramme H-R des étoiles de
l'amas en utilisant seulement la magnitude apparente (m). Le diagramme, par rapport à un diagramme
en magnitude absolue (M), se trouve simplement décalé le long de l'axe vertical de la quantité :
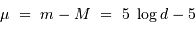
(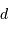 étant exprimée en parsec).
étant exprimée en parsec).
En comparant la position en magnitude apparente de la séquence principale de l'amas à un diagramme de référence calibré en magnitude absolue, on obtient donc une mesure de sa distance. De même, en comparant les positions en magnitude apparente des séquences principales de différents amas, on obtient directement leurs distances relatives.
On note cependant que, comme pour la parallaxe spectroscopique, il faut en plus connaître la composition chimique des étoiles (que l'on caractérise par leur métallicité, c'est-à-dire le taux d'éléments plus lourds que l'hélium présents dans leur atmosphère) pour avoir une mesure réellement précise à mieux que quelques dixièmes de magnitude.
La distance de l'amas M67
L'appliquette ci-jointe permet l'ajustement des étoiles de l'amas M67 sur la séquence principale.
- Ajuster au-mieux les étoiles de l'amas sur la séquence principale, en positionnant au mieux les étoiles de l'amas juste au dessus de la séquence principale (ZAMS = zero age main sequence)
- Éventuellement corriger du rougissement observationnel, en décalant le jeu d'étoiles de M67 selon l'axe des indices de couleur.
- Procéder à un ajustement plus fin en agrandissant la région intéressante ; pour ce faire, sélectionner cette région avec la souris.
- Déduire du module de distance
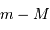 la distance de l'amas.
la distance de l'amas.

Solution :
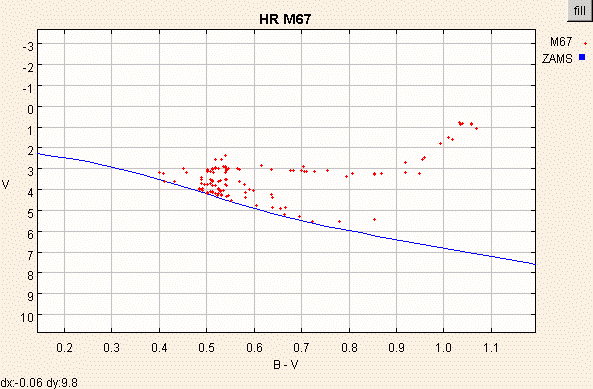
Le module de distance de M67 est voisin de 9.8, pour un rougissement de 0.06.
Crédit :
ASM
Les Pléiades
Même exercice que ci-dessus, avec les étoiles de l'amas des Pléiades.

Solution :
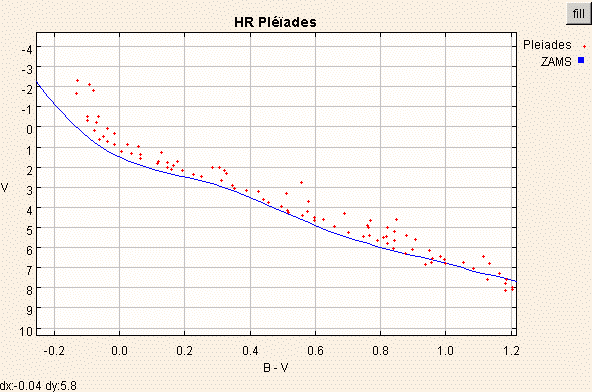
Le module de distance des Pléiades est voisin de 6.0 pour un rougissement de 0.04.
Crédit :
ASM

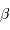 Orion), de type spectral B8 et de classe de luminosité Ia, avec une température de surface de 11500 K, on trouvera par exemple une magnitude absolue de
Orion), de type spectral B8 et de classe de luminosité Ia, avec une température de surface de 11500 K, on trouvera par exemple une magnitude absolue de 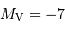 , ce qui, confronté à la mesure de sa magnitude apparente de 0.14, lui confère une distance de 268 pc.
, ce qui, confronté à la mesure de sa magnitude apparente de 0.14, lui confère une distance de 268 pc.
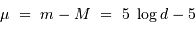
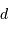 étant exprimée en parsec).
étant exprimée en parsec).
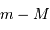 la distance de l'amas.
la distance de l'amas.

