
|
La magnitude absolue 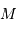 est la magnitude conventionnelle qu'aurait l'étoile si sa distance était ramenée, par définition à 10 pc.
est la magnitude conventionnelle qu'aurait l'étoile si sa distance était ramenée, par définition à 10 pc.
Il faut lier l'éclairement apparent de l'étoile à sa distance 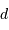 à la Terre,
ce que l'on fait avec la
luminosité
à la Terre,
ce que l'on fait avec la
luminosité 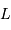 de l'étoile, mesurant la puissance totale
rayonnée par l'étoile :
de l'étoile, mesurant la puissance totale
rayonnée par l'étoile :
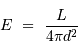
Le flux d'une étoile varie comme l'inverse du carré de la distance, donc dans un système de magnitude donné, la relation entre magnitudes absolue et apparente s'écrit :
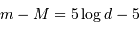
| Objet | 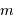 | 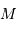 | 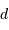 (pc) (pc) |
| soleil | -26.7 | 4.9 | |
| Sirius | -1.45 | 1.4 | 2.7 |
| Véga | 0.00 | 0.5 | 8.1 |
| Antarès | 1.00 | -4.8 | 130 |
| Mimosa | 1.26 | -4.7 | 150 |
| Adhara | 1.50 | -5.0 | 200 |
La quantité 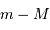 porte le nom de module de distance. En reliant la distance à une différence de magnitude, ce module indique la distance en échelle logarithmique.
porte le nom de module de distance. En reliant la distance à une différence de magnitude, ce module indique la distance en échelle logarithmique.
| Objet | module de distance | distance au Soleil (pc) |
| référence | 0 | 10 |
| L'amas des Hyades | 3.3 | 48 |
| Les Nuages de Magellan | 18.5 | 50 000 |
| La galaxie d'Andromède | 24.1 | 890 000 |
Le module de distance est nul, par définition, pour une distance de 10 pc ; il vaut 5 pour une distance de 100 pc, 10 pour une distance de 1000 pc.
Pour passer de la magnitude apparente à la magnitude absolue, on est amené à corriger, en plus de la distance, les effets dus à une éventuelle absorption interstellaire. Cette absorption est provoquée par divers éléments (poussières, gaz) présent sur la ligne de visée. Alors, la magnitude absolue s'exprime en fonction de la magnitude apparente par :
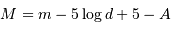
Le terme d'absorption 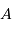 ne peut être que positif ; ne pas en tenir compte conduit à surestimer la magnitude absolue, càd à sous-estimer la luminosité de l'objet.
ne peut être que positif ; ne pas en tenir compte conduit à surestimer la magnitude absolue, càd à sous-estimer la luminosité de l'objet.
A l'opposé de la magnitude monochromatique, la magnitude bolométrique mesure l'énergie rayonnée sur l'ensemble du spectre électromagnétique. Mesurer une telle magnitude n'est pas chose aisée, et s'obtient le plus souvent par extrapolation à partir de la magnitude absolue mesurée dans quelques bandes spectrales.