 RR Lyrae, amas globulaires et Voie Lactée
RR Lyrae, amas globulaires et Voie Lactée
Difficulté : ☆☆
Temps : 1.5 h
On se propose de mesurer la taille et la position du centre de notre Galaxie, la Voie Lactée, à partir des amas globulaires (méthode de Shapley, 1914).
On dispose de diagrammes
magnitude-couleur (V,
B-V) de différents amas globulaires.
Les coordonnées galactiques 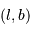 (données en deg) de ces amas permettent de repérer leur direction dans le ciel. On connaît de plus l'extinction totale (la correction d'absorption, donnée en magnitude) due au gaz et aux poussières rencontrés le long de chaque ligne de visée.
(données en deg) de ces amas permettent de repérer leur direction dans le ciel. On connaît de plus l'extinction totale (la correction d'absorption, donnée en magnitude) due au gaz et aux poussières rencontrés le long de chaque ligne de visée.
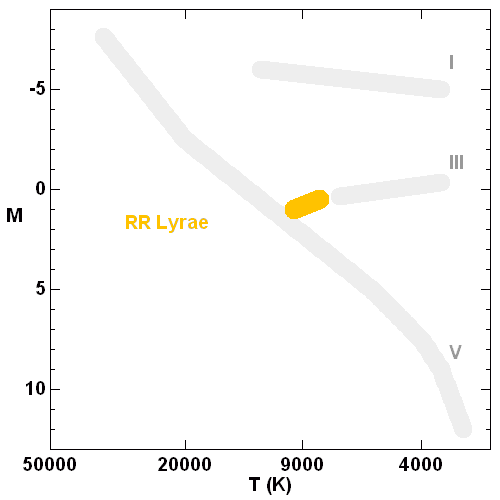
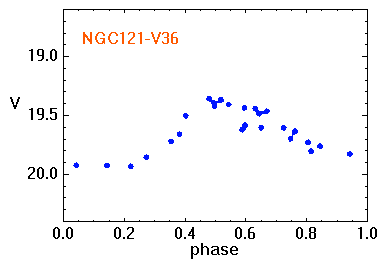
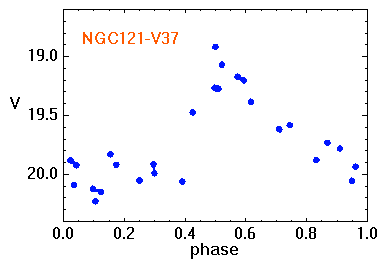
Le but est de déterminer la position des amas globulaires en utilisant les étoiles RR-Lyrae comme indicateurs de distance. A partir de sa distance et de sa direction, on peut localiser chaque amas dans l'espace et déterminer le centre de symétrie du système des amas globulaires. On obtient ainsi la position du centre de notre Galaxie par rapport au Soleil, ainsi qu'une mesure des dimensions de la Voie Lactée.
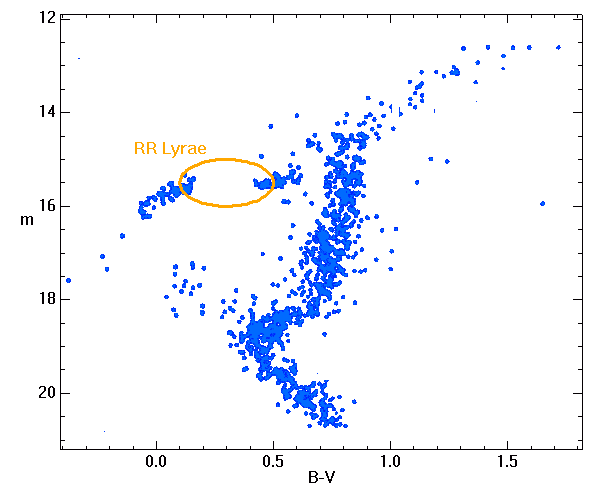
Le diagramme magnitude-couleur des amas globulaires comporte une branche horizontale avec une zone vide entre B-V=0.2 et 0.4 environ, où sont localisées les étoiles variables RR-Lyrae. Sur chaque diagramme, à lire avec les appliquettes ci-jointes, on peut, selon les conditions d'observation, reconnaître la série principale, la branche des géantes, la branche horizontale et la région vide.
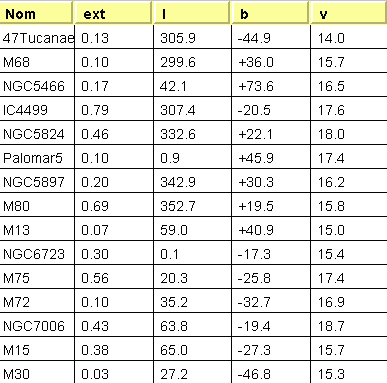
47Tuc 
M68 
NGC5466 
IC4499 
NGC5824 
Palomar5 
NGC5897 
M80 
M13 
NGC6723 
M75 
M72 
NGC7006 
M15 
M30 
Tableau 
Question 1)
Dans quels amas ces séquences sont-elles plus difficilement discernables ? Pourquoi ?
Identifier les diagrammes bruités, et ceux pour lesquels les objets de faible magnitude n'ont pas été observés.
Question 2)
Les diagrammes HR de IC4499, NGC5824, M75 ou NGC7006 apparaissent très bruités.
Montrer que cela est lié à leur position dans la Voie Lactée.
S'intéresser à leur latitude galactique 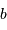 .
.
Question 3)
Mesurer, pour les amas où cela est possible, la magnitude apparente visuelle observée 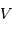 correspondant au bord bleu du trou de la branche horizontale, à 0.1 magnitude près.
correspondant au bord bleu du trou de la branche horizontale, à 0.1 magnitude près.

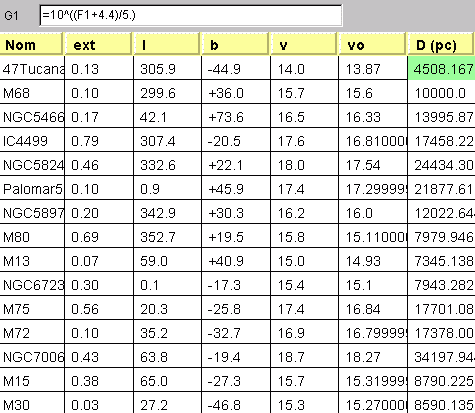
Remplir la colonne V du tableau à l'aide de ces données (ne simplement rien marquer pour les amas éventuellement laissés de côté).
Le bord bleu est, dans un diagramme B-V, sur la gauche.
Question 4)
Compte tenu de la correction d'extinction interstellaire, en déduire la magnitude apparente moyenne corrigée 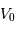 des RR-Lyrae dans chacun des amas.
des RR-Lyrae dans chacun des amas.
La correction de l'extinction module-t-elle les magnitude à la hausse ou à la baisse ?
Question 5)
En adoptant pour les RR-Lyrae une magnitude absolue moyenne 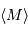 égale à +0.6, en déduire la distance
égale à +0.6, en déduire la distance 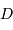 (en parsec) de chaque amas. On rappelle l'expression du module de distance :
(en parsec) de chaque amas. On rappelle l'expression du module de distance :
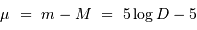
avec la distance exprimée en parsec. Quelle est la précision sur 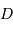 si l'incertitude sur
si l'incertitude sur 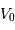 est de 0.1 magnitude ?
est de 0.1 magnitude ?
Question 6)
Déduire des coordonnées galactiques 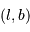 et de la distance
et de la distance 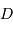 (question 5) les coordonnées rectangulaires
(question 5) les coordonnées rectangulaires 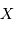 ,
, 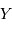 , et
, et 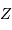 (en parsec) de chaque amas.
(en parsec) de chaque amas.
On utilise les relations :
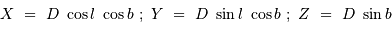
Question 7)
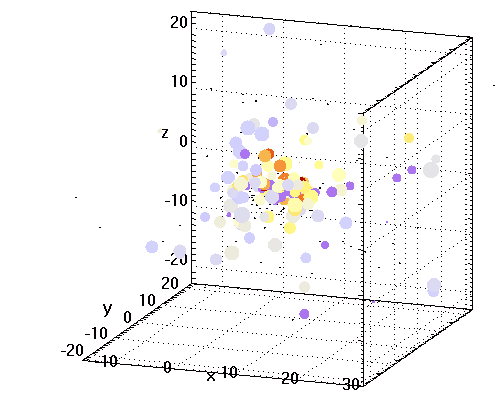
Analyser la répartition des amas dans le plan (SX, SZ), en réalisant une coupe de notre galaxie vue par la tranche, passant par le Soleil S suivant SX.
Quelles sont les dimensions du halo ? Quelle est la position du centre de symétrie du système ?
(calculer les valeurs moyennes de X et Z). Comparer aux valeurs admises actuellement : la Galaxie a un diamètre de 30 kpc ; le Soleil se trouve à 8.5 kpc du centre.
L'appliquette ne permet (malheureusement) pas de calculer les moyennes demandées.
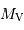
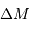
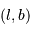 (données en deg) de ces amas permettent de repérer leur direction dans le ciel. On connaît de plus l'extinction totale (la correction d'absorption, donnée en magnitude) due au gaz et aux poussières rencontrés le long de chaque ligne de visée.
(données en deg) de ces amas permettent de repérer leur direction dans le ciel. On connaît de plus l'extinction totale (la correction d'absorption, donnée en magnitude) due au gaz et aux poussières rencontrés le long de chaque ligne de visée.

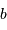 .
.
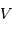 correspondant au bord bleu du trou de la branche horizontale, à 0.1 magnitude près.
correspondant au bord bleu du trou de la branche horizontale, à 0.1 magnitude près.
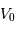 des RR-Lyrae dans chacun des amas.
des RR-Lyrae dans chacun des amas.
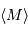 égale à +0.6, en déduire la distance
égale à +0.6, en déduire la distance 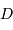 (en parsec) de chaque amas. On rappelle l'expression du module de distance :
(en parsec) de chaque amas. On rappelle l'expression du module de distance :
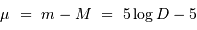
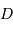 si l'incertitude sur
si l'incertitude sur 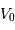 est de 0.1 magnitude ?
est de 0.1 magnitude ?
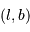 et de la distance
et de la distance 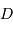 (question 5) les coordonnées rectangulaires
(question 5) les coordonnées rectangulaires 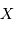 ,
, 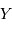 , et
, et 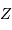 (en parsec) de chaque amas.
(en parsec) de chaque amas.
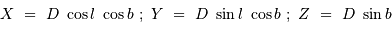
 ). Ils souffrent d'une importante extinction. Ces deux effets (proximité du plan Galactique + extinction importante) se traduisent par une plus grande incertitude sur les magnitudes et un plus grand risque de contamination par des étoiles d'avant-plan appartenant au disque de la Voie Lactée.
). Ils souffrent d'une importante extinction. Ces deux effets (proximité du plan Galactique + extinction importante) se traduisent par une plus grande incertitude sur les magnitudes et un plus grand risque de contamination par des étoiles d'avant-plan appartenant au disque de la Voie Lactée.
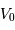 est donc nécessairement plus petite que la magnitude observée
est donc nécessairement plus petite que la magnitude observée 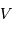 :
:
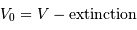
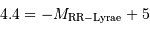 .
.
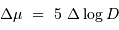
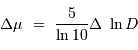
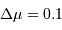 :
:
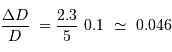
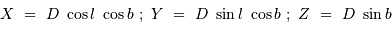
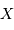 , par :
, par :
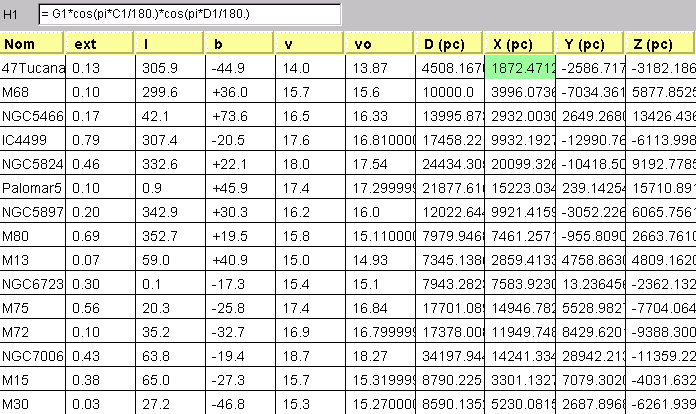
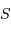 , situé dans la direction du centre Galactique. Les valeurs moyennes des positions en X et en Z donnent respectivement 8770 pc et 490 pc. Compte tenu des incertitudes sur les mesures, le centre de symétrie est donc situé dans le plan Galactique
, situé dans la direction du centre Galactique. Les valeurs moyennes des positions en X et en Z donnent respectivement 8770 pc et 490 pc. Compte tenu des incertitudes sur les mesures, le centre de symétrie est donc situé dans le plan Galactique 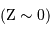 à environ 8.7 kpc
(28 600 années de lumière) du Soleil, en bon accord avec les valeurs admises aujourd'hui.
à environ 8.7 kpc
(28 600 années de lumière) du Soleil, en bon accord avec les valeurs admises aujourd'hui.