Astrométrie
Il est possible de détecter le mouvement de l'étoile perpendiculairement à la ligne de visée, c'est-à-dire sur
la sphère céleste, et d'en déduire les caractéristiques de
la planète et de son orbite.
Déplacement astrométrique du Soleil dû à Jupiter
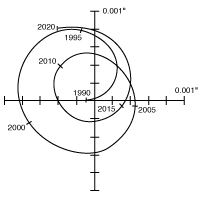
Déplacement du Soleil sous l'effet des mouvements planétaires (Jupiter et Saturne principalement), vu à une distance de 10 pc.
L'amplitude de ce déplacement est de 500 microsecondes d'arc (
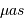
). Le déplacement dû à la Terre présenterait une amplitude de
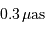
à la même distance.
Crédit :
NASA
 Objectifs
Objectifs
L'astrométrie s'intéresse à la position des astres sur la sphère céleste. Cette technique peut être sensible à la modulation de la position d'une étoile légèrement perturbée par la présence d'une planète.
Astrométrie
Il est possible de détecter le mouvement de l'étoile
perpendiculairement à la ligne de visée, c'est-à-dire sur
la sphère céleste, et d'en déduire les caractéristiques de la
planète et de son orbite.
On se limite au cas d'une orbite
circulaire, mais bien sûr cette méthode s'applique aussi à la détection
de planètes sur des orbites elliptiques. Le mouvement de l'étoile
projeté sur le plan du ciel, c'est-à-dire sur le plan perpendiculaire à
la ligne de visée, est une ellipse de demi-grand axe 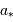 . Comme
la distance
. Comme
la distance 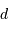 à l'étoile est grande devant
à l'étoile est grande devant 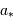 , la déviation
angulaire correspondante est
, la déviation
angulaire correspondante est 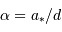 , ou encore :
, ou encore :
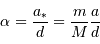
avec 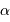 exprimé
seconde d'arc,
exprimé
seconde d'arc, 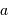 le
rayon de l'orbite de la planète (en UA) et
le
rayon de l'orbite de la planète (en UA) et 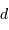 la distance
Soleil-étoile. La masse
la distance
Soleil-étoile. La masse 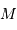 de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire
de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire 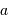 de la périodicité du
mouvement, et donc la masse de la planète
de la périodicité du
mouvement, et donc la masse de la planète 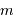 de la mesure de
de la mesure de 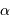 .
.
En pratique, la variation de la position d'un astre sur la sphère céleste n'est pas mesurée de façon absolue, mais différentiellement par rapport à un objet du champ, angulairement proche mais très lointain en distance, dont la position reste fixe.

Diagramme masse-distance, montrant les performances de la détection astrométrique, fonction de la précision de mesure (respectivement 10, 1 et 0.05 milliseconde d'arc). Les triangles rouges marquent les exoplanètes déjà détectées.
Crédit :
ASM
Systèmes pouvant être détectés par cette méthode
Les mesures faites à l'heure actuelle depuis le sol ont une précision d'une milliseconde d'arc (mas), et devraient atteindre 10 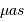 dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des zones habitables (i.e.
dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des zones habitables (i.e. 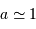 UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
 Petite révision sur la formation d'image
Petite révision sur la formation d'image
Difficulté : ☆
Temps : 30 min
Un astronome extraterrestre regarde notre système solaire à une distance de 10 AL de notre Soleil. On souhaite dimensionner le télescope dont il aurait besoin pour distinguer Jupiter autour du Soleil.
On suppose le pouvoir de résolution de l'appareil limité par la seule diffraction : la tache de diffraction vaut angulairement 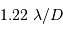 radian, où
radian, où 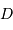 est le diamètre du télescope.
est le diamètre du télescope.
Pour la suite, on prendra 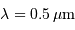 .
.
Question 1)
Déterminer la distance angulaire maximale 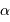 entre le soleil et Jupiter
entre le soleil et Jupiter 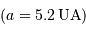 .
.
Rappel : 1 AL = 63 000 UA.
Question 2)
Déterminer 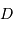 , le diamètre minimum du collecteur nécessaire.
, le diamètre minimum du collecteur nécessaire.
Un objet est résolu spatialement si sa taille angulaire est supérieure à la taille de la tache de diffraction.
Question 3)
Cela est-il suffisant?
S'intéresser au rapport des flux respectifs du Soleil et de Jupiter.
 Astrométrie
Astrométrie
Difficulté : ☆☆
Temps : 40 min
Le mouvement apparent d'une étoile voisine du soleil, corrigé de la parallaxe annuelle, est a priori rectiligne uniforme en l'absence de perturbation. On cherche à quantifier l'influence d'un compagnon planétaire.
On observe un système binaire composé d'une étoile de masse 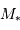 et d'une planète de masse
et d'une planète de masse 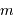 ( avec
( avec 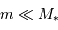 ) de rayon orbital
) de rayon orbital 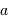 .
.
Question 1)
Justifier le caractère rectiligne et uniforme du mouvement stellaire, en l'absence de compagnon.
Un mouvement rectiligne uniforme est un mouvement non perturbé par quoi
que ce soit.
Question 2)
Exprimer l'amplitude de la perturbation angulaire maximale 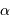 de la position de l'étoile, située à une distance
de la position de l'étoile, située à une distance 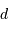 du Soleil.
du Soleil.
Question 3)
Retrouver l'expression :
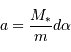
Définir le centre de masse.
Etablir 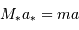
Question 4)
A quelle distance 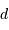 se situe l'étoile si sa parallaxe annuelle vaut 0.1" ?
se situe l'étoile si sa parallaxe annuelle vaut 0.1" ?
Le parsec est défini comme étant la distance d'une étoile ayant une parallaxe de 1".
Question 5)
Quelles planètes du système solaire, supposé vu à 10 pc, pourrait-on détecter, si l'on est capable de mesurer des variations de position à 0.01" ou 0.001" près ?
Compléter le diagramme ci-joint, positionnant les objets en fonction de leur masse 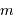 et de leur demi-grand axe
et de leur demi-grand axe 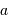 , en définissant la frontière qui marque la limite de détectabilité
(rappel
, en définissant la frontière qui marque la limite de détectabilité
(rappel 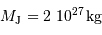 ).
).
Diagramme a-msin i
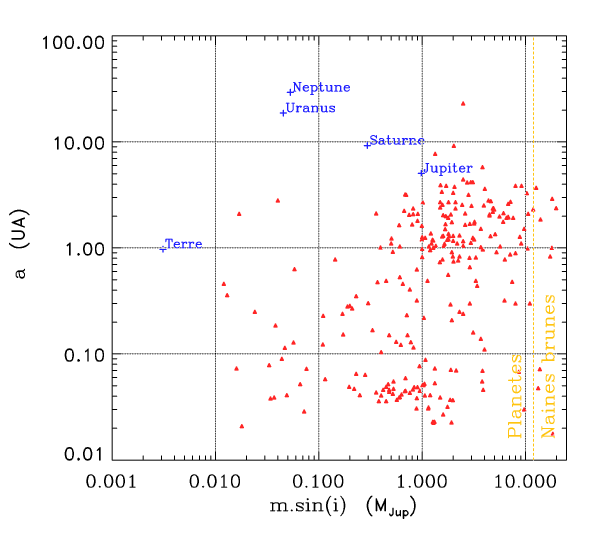
Crédit :
ASM
Traduire la relation établie précédemment entre 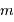 et
et 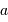 , et l'exprimer dans le système d'unités (UA, masse de Jupiter).
, et l'exprimer dans le système d'unités (UA, masse de Jupiter).
Question 6)
A terme, on imagine être capable de mesurer des écarts de position 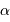 avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme
avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme 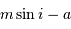 , pour un système à 10 pc et
, pour un système à 10 pc et 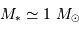 .
.
C'est la même chose que précédemment. Seule l'application numérique change.
Question 7)
Quelles planètes du système solaire deviennent ainsi détectables ?
Si les graphes ont été dressés, la réponse n'est plus qu'une question de domaine.
- Question 1
Aide :
Un mouvement rectiligne uniforme est un mouvement non perturbé par quoi
que ce soit.
Solution :
L'étoile observée est isolée, et donc elle obéit au principe de Galilée.
- Question 2
Aide :
Faire un schéma.
Solution :
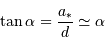
avec 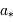 étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
- Question 3
Aide :
Définir le centre de masse.
Aide :
Etablir 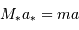
Solution :
D'après la définition du barycentre 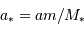 . Alors :
. Alors :
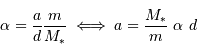
- Question 4
Aide :
Le parsec est défini comme étant la distance d'une étoile ayant une parallaxe de 1".
Solution :
Une étoile ayant une parallaxe de 0.1" est, par définition, à 10 pc.
- Question 5
Aide :
Traduire la relation établie précédemment entre 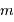 et
et 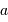 , et l'exprimer dans le système d'unités (UA, masse de Jupiter).
, et l'exprimer dans le système d'unités (UA, masse de Jupiter).
Aide :
Le produit 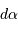 , avec
, avec 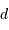 en pc et
en pc et 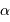 en seconde d'arc, donne directement une distance en UA.
en seconde d'arc, donne directement une distance en UA.
Solution :
On traite l'équation :
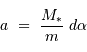
en tenant en compte que le produit 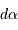 , avec
, avec 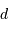 en pc et
en pc et 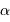 en " donne une distance en UA directement, par définition. En prenant
en " donne une distance en UA directement, par définition. En prenant 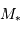 directement en masse jovienne (
directement en masse jovienne (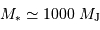 ), on obtient dans le système d'unités (UA,
), on obtient dans le système d'unités (UA, 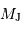 ), pour
), pour 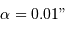 :
:
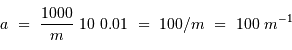
En échelle logarithmique, cette équation définit une droite de pente -1 ; elle passe par le point 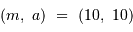 .
.
Pour une précision de 1 mas (1 millième de seconde d'arc), la courbe obtenue est définie par :
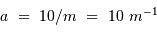
Parallèle à la précédente, elle contient le point
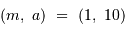 .
.
Comme le montre le diagramme ci-joint, aucune planète du système solaire n'est ainsi détectable à ce niveau de précision astrométrique.
Diagramme a-msin i
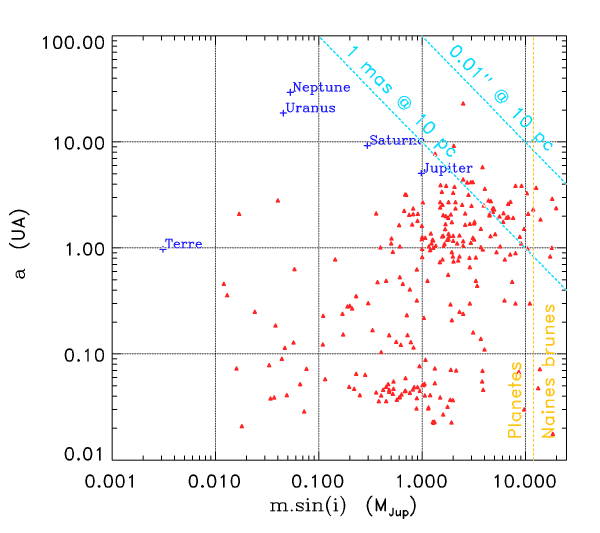
Crédit :
ASM
- Question 6
Aide :
C'est la même chose que précédemment. Seule l'application numérique change.
Solution :
Par rapport au cas précédent, le gain en précision d'un facteur 20 déplace la
limite vers les faibles masses, passant p.ex. par le point
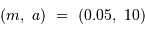 .
.
Planètes détectables
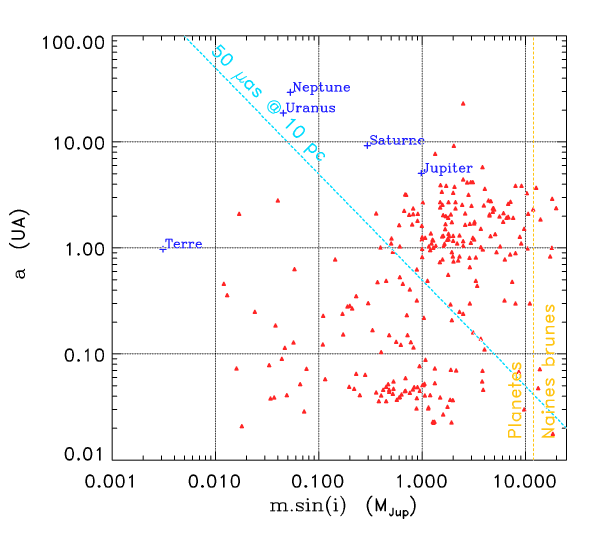
Crédit :
ASM
- Question 7
Aide :
Si les graphes ont été dressés, la réponse n'est plus qu'une question de domaine.
Solution :
Planètes détectables : Jupiter, Saturne, Uranus et Neptune. Seules les planètes géantes sont donc détectables, pas la Terre !
Planètes détectables
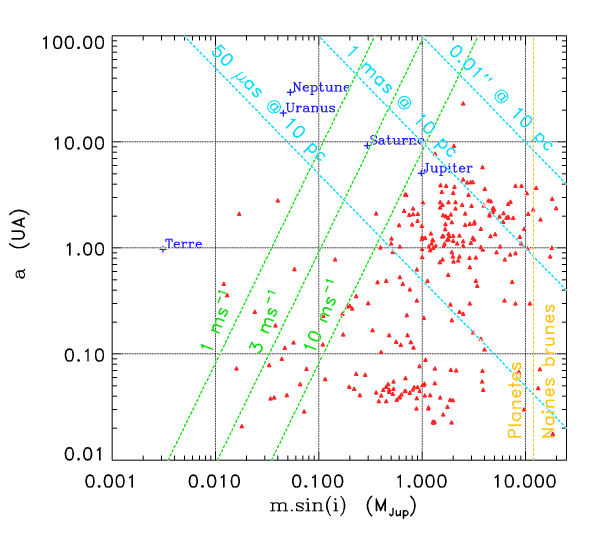
Crédit :
ASM

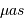 ). Le déplacement dû à la Terre présenterait une amplitude de
). Le déplacement dû à la Terre présenterait une amplitude de 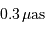 à la même distance.
à la même distance.
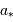 . Comme
la distance
. Comme
la distance 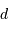 à l'étoile est grande devant
à l'étoile est grande devant 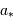 , la déviation
angulaire correspondante est
, la déviation
angulaire correspondante est 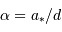 , ou encore :
, ou encore :
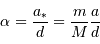
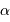 exprimé
seconde d'arc,
exprimé
seconde d'arc, 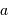 le
rayon de l'orbite de la planète (en UA) et
le
rayon de l'orbite de la planète (en UA) et 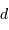 la distance
Soleil-étoile. La masse
la distance
Soleil-étoile. La masse 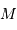 de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire
de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire 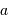 de la périodicité du
mouvement, et donc la masse de la planète
de la périodicité du
mouvement, et donc la masse de la planète 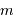 de la mesure de
de la mesure de 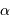 .
.

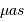 dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des
dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des 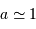 UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
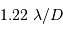 radian, où
radian, où 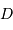 est le diamètre du télescope.
est le diamètre du télescope.
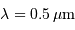 .
.
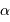 entre le soleil et Jupiter
entre le soleil et Jupiter 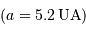 .
.
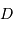 , le diamètre minimum du collecteur nécessaire.
, le diamètre minimum du collecteur nécessaire.
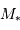 et d'une planète de masse
et d'une planète de masse 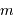 ( avec
( avec 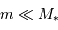 ) de rayon orbital
) de rayon orbital 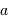 .
.
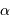 de la position de l'étoile, située à une distance
de la position de l'étoile, située à une distance 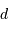 du Soleil.
du Soleil.
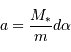
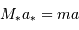
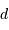 se situe l'étoile si sa
se situe l'étoile si sa 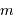 et de leur demi-grand axe
et de leur demi-grand axe 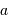 , en définissant la frontière qui marque la limite de détectabilité
(rappel
, en définissant la frontière qui marque la limite de détectabilité
(rappel 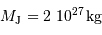 ).
).

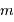 et
et 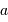 , et l'exprimer dans le système d'unités (UA, masse de Jupiter).
, et l'exprimer dans le système d'unités (UA, masse de Jupiter).
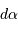 , avec
, avec 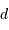 en pc et
en pc et 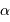 en seconde d'arc, donne directement une distance en UA.
en seconde d'arc, donne directement une distance en UA.
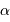 avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme
avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme 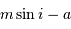 , pour un système à 10 pc et
, pour un système à 10 pc et 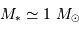 .
.
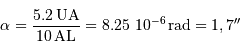
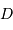 du collecteur est atteint lorsque la tache de diffraction est égale la distance angulaire maximum
du collecteur est atteint lorsque la tache de diffraction est égale la distance angulaire maximum 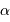 entre le soleil et Jupiter :
entre le soleil et Jupiter :
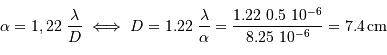
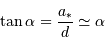
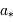 étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
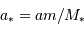 . Alors :
. Alors :
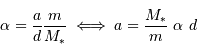
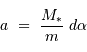
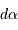 , avec
, avec 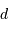 en pc et
en pc et 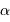 en " donne une distance en UA directement, par définition. En prenant
en " donne une distance en UA directement, par définition. En prenant 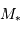 directement en masse jovienne (
directement en masse jovienne (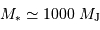 ), on obtient dans le système d'unités (UA,
), on obtient dans le système d'unités (UA, 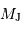 ), pour
), pour 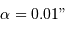 :
:
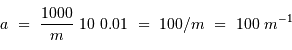
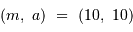 .
.
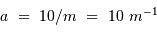
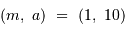 .
.

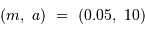 .
.

