Elargissement rotationnel
La rotation de l'étoile mélange, sauf à résoudre spatialement ou spectralement l'objet, les diverses régions qui toutes contribuent au flux stellaire. Il s'ensuit un élargissement des raies.


La rotation de l'étoile, en codage Doppler : une couleur rouge signe un éloignement radial ; le bleu un rapprochement. Un axe de rotation quasi perpendiculaire au plan du ciel entraîne une très faible signature, car la projection géométrique amoindrit la composante radiale de la vitesse de rotation.
Crédit :
ASM
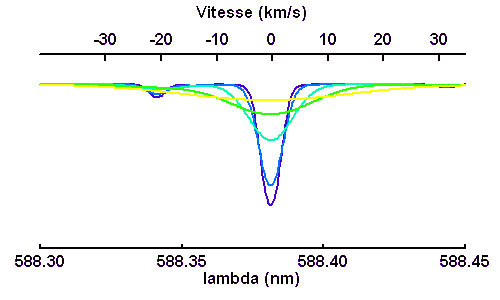
Elargissement rotationnel (vitesse équatoriale de 1, 2, 5, 10, 20 ou 40 km/s. La conservation de l'énergie (l'énergie qui manque dans la raie) entraîne une très nette diminution de la profondeur de la raie lorsque la vitesse rotationnelle augmente. Pour les rotateurs rapides, une raie fine devient invisible.
Crédit :
ASM
Elargissement en température et rotationnel
L'élargissement des raies due à la rotation de l'étoile modifie drastiquement l'allure d'un spectre, comme le montre les simulations d'observation à
faible ou
grande résolution spectrale.
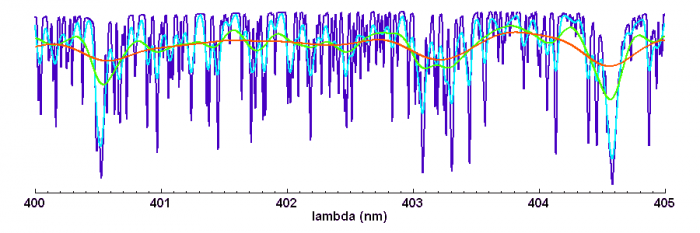
Elargissement rotationnel (
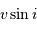
de 5, 20, 80 ou 200 km/s). Spectre d'une étoile F9 à grande résolution spectrale (R=120000)
Crédit :
ASM
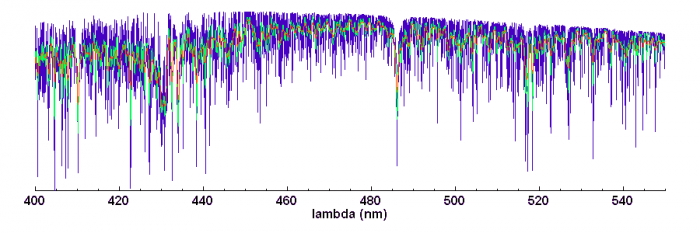
Elargissement rotationnel (
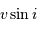
de 10, 80 ou 200 km/s. Spectre d'une étoile F9 à faible résolution spectrale (R=8000)
Crédit :
ASM
 Objectifs
Objectifs
La largeur des raies stellaires est liée aux champs de vitesse Doppler.
Agitation thermique
Dans le cadre de la théorie cinétique du gaz parfait, la distribution de vitesse est donnée par :
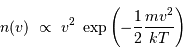
avec 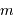 la masse atomique moyenne et
la masse atomique moyenne et 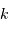 la constante de Boltzmann.
la constante de Boltzmann.
La largeur à mi-hauteur de cette distribution est de l'ordre de 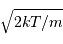 , du même ordre de grandeur que les vitesses moyenne ou la plus probable.
, du même ordre de grandeur que les vitesses moyenne ou la plus probable.
Avec une température stellaire entre typiquement 4000 et 40000 K, les vitesses
d'agitation thermique sont de l'ordre de 8 à 25 km/s : elles concourent à un sensible élargissement des raies.
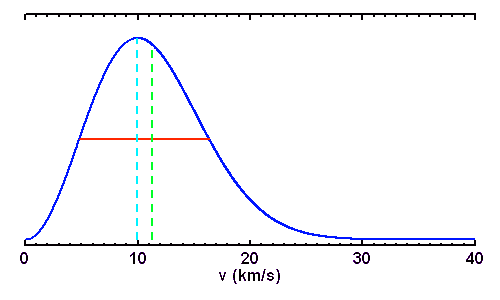
Distribution de vitesse de Boltzman. La vitesse la plus probable (bleu clair) est voisine de la vitesse moyenne (vert), et elles sont toutes deux du même ordre de grandeur que la dispersion caractéristique en vitesse (rouge).
Crédit :
ASM
Rotation stellaire
La rotation stellaire participe également à l'élargissement des raies stellaires.
Le paramètre important pour mesurer cet effet est donné par la projection du vecteur vitesse de rotation équatorial sur la ligne de visée :
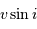 .
Les valeurs typiques de rotation varient de quelques km/s (rotateurs lents, tels le Soleil) à plusieurs centaines de km/s. Dans ce dernier cas, les signatures spectrales deviennent très peu marquées.
.
Les valeurs typiques de rotation varient de quelques km/s (rotateurs lents, tels le Soleil) à plusieurs centaines de km/s. Dans ce dernier cas, les signatures spectrales deviennent très peu marquées.
En effet, une raie fine à vitesse rotationnelle non nulle s'élargit par effet Doppler. Par application de la conservation de l'énergie, le manque de photons dans la raie est conservé, et donc l'élargissement de la raie s'accompagne d'une moindre profondeur.
Élargissement des raies stellaires selon la vitesse de rotation stellaire
La conservation de l'énergie (l'énergie qui manque dans la raie) entraîne une très nette diminution de la profondeur de la raie lorsque la vitesse rotationnelle augmente. Pour les rotateurs rapides, une raie fine devient invisible.
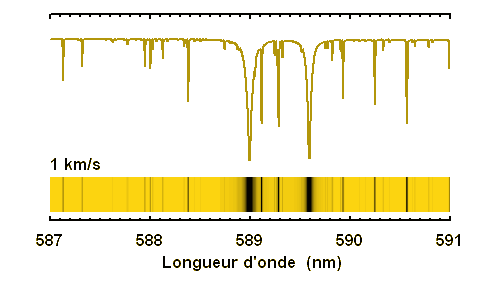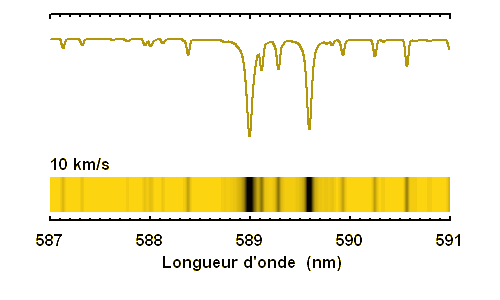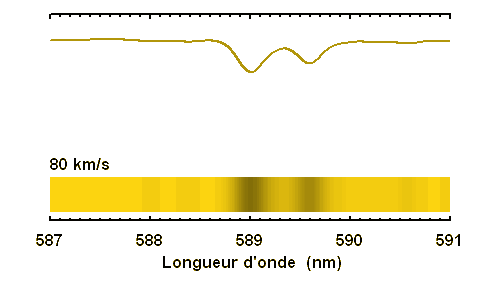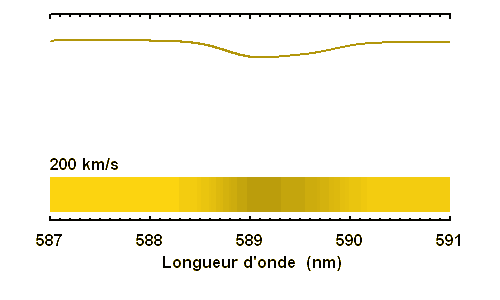
La conservation de l'énergie (l'énergie qui manque dans la raie) entraîne une très nette diminution de la profondeur de la raie lorsque la vitesse rotationnelle augmente. Pour les rotateurs rapides, une raie fine devient invisible.
Crédit :
ASM
Elargissement des raies stellaires selon la direction de l'inclinaison
L'animation montre comme varie l'élargissement rotationnel des raies stellaires avec l'angle d'inclinaison  . Lorsque l'axe de rotation de l'étoile se confond avec la ligne de visée, il n'y a pas d'élargissement rotationnel.
. Lorsque l'axe de rotation de l'étoile se confond avec la ligne de visée, il n'y a pas d'élargissement rotationnel.
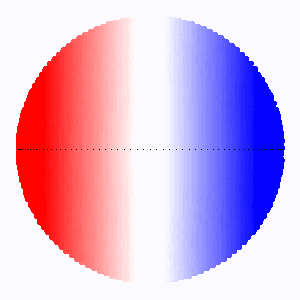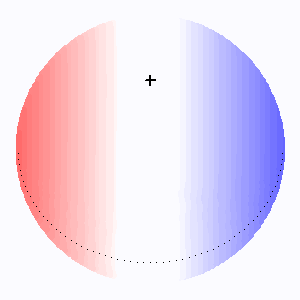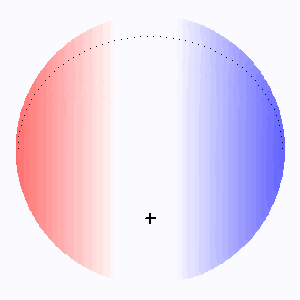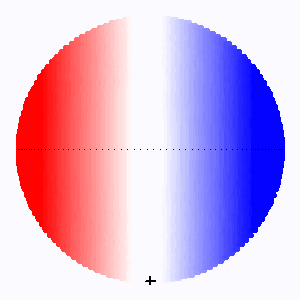
L'élargissement rotationnel (codé ici en couleur d'autant plus rouge/bleue que la vitesse d'éloignement/rapprochement est grande) dépend du facteur
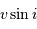
, et varie ici avec l'inclinaison

sur l'axe de visée.
Crédit :
ASM
Mesure de rotation par sondage radar
Les sondages radar permettent de mesurer la rotation d'un corps, comme le montre l'animation ci-jointe.
L'onde plane incidente parcourt l'objet du point subterrestre jusqu'au limbe, en une durée 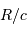 (
(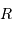 est le rayon de l'objet,
est le rayon de l'objet, 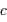 la célérité de la lumière) et donc scanne le champ de vitesse rotationnel.
la célérité de la lumière) et donc scanne le champ de vitesse rotationnel.
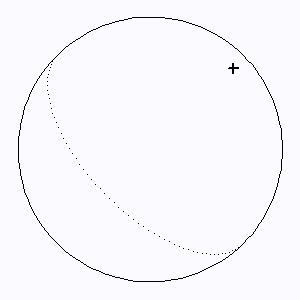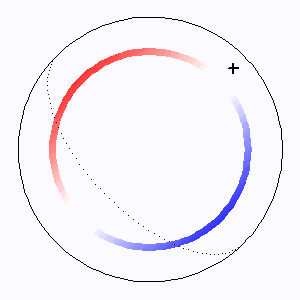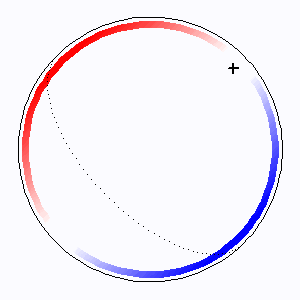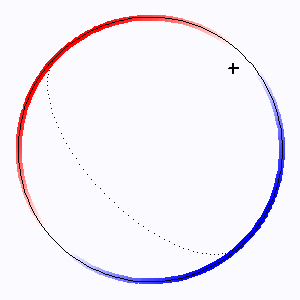
Sondage d'un objet, supposé sphérique, par une onde plane radar. L'animation suppose un pas de temps équidistant. Les premières mesures, en projection sur le plan du ciel, parcourent
rapidement l'objet, plus lentement ensuite pour les régions proches du limbe, mais alors l'excursion en vitesse Doppler devient maximale
Crédit :
ASM
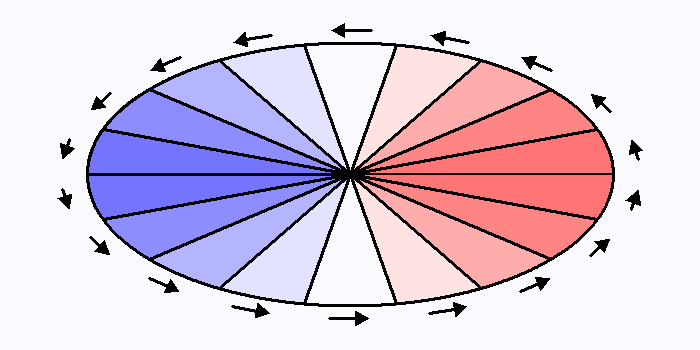
Disque en rotation.
Crédit :
ASM
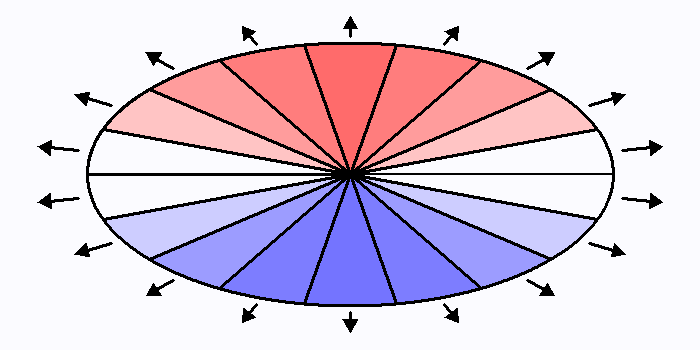
Disque en expansion
Crédit :
ASM
 Mesure de la période de rotation de Mercure
Mesure de la période de rotation de Mercure
Difficulté : ☆☆
Temps : 1.5 heure
Le but de l'exercice est d'interpréter les observations radio de la planète Mercure, menées au radio-télescope d'Arecibo en 1965
(Dyce et al. 1965, Astronomical Journal 72, 351-359). Il s'agissait alors de mesurer la période de rotation propre de Mercure, et de déterminer si elle était égale ou non à la période de rotation orbitale.
| demi-grand axe | 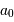 | 0.39 UA |
| révolution sidérale | 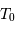 | 88 j |
| rayon | 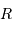 | 2420 km |
| diamètre du radiotél. | 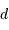 | 305 m |
| fréquence émise | 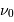 | 430 MHz |

Question 1)
Propagation :
L'écho d'un signal radio émis par le télescope d'Arecibo et
réfléchi par Mercure est réceptionné 616.125 s après son
émission. En déduire la distance Terre-Mercure 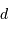 lors de l'observation,
et représenter la position relative de ces 2 planètes et du Soleil. Les observations effectuées pourraient-elles être menées en lumière visible ?
lors de l'observation,
et représenter la position relative de ces 2 planètes et du Soleil. Les observations effectuées pourraient-elles être menées en lumière visible ?
L'onde radio parcourt le vide à la célérité de la lumière.
Attention au doublement de la distance par aller-retour.
Question 4)
L'écho :
Le document ci-joint (Dyce et al. 1965)
montre l'étalement en fréquence de l'écho en
fonction du retard à la réception.
Comparer le retard maximal théorique à celui enregistré, et interpréter
le désaccord. En déduire, que la relation entre 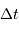 et
et 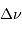 se réduit, pour les mesures effectuées, à
se réduit, pour les mesures effectuées, à 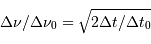 Comment interpréter les variations temporelles d'intensité du signal ?
Comment interpréter les variations temporelles d'intensité du signal ?
Estimer 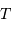 , la période de rotation propre de Mercure.
, la période de rotation propre de Mercure.
On pose 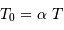 . Quelle signification donner à
. Quelle signification donner à 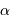 ?
De quelle fraction simple
?
De quelle fraction simple 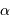 est-il proche ? Est-ce un hasard ?
est-il proche ? Est-ce un hasard ?
Pourquoi les données présentant un plus fort retard ne sont-elles pas
facilement exploitables ?
Etudier les conditions de réflexion de l'onde, en supposant valide l'optique géométrique.
Montrer que les dates effectives d'observations vérifient 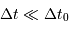 , et en tirer les conséquences.
, et en tirer les conséquences.
Question 5)
La puissance de l'écho :
Quelle fraction du signal Mercure intercepte-t-il ? [on se contentera d'un ordre de grandeur grossier, en supposant que le flux radar est homogène dans un champ d'angle solide égal au lobe principal de diffraction ; un calcul précis est hors de portée de la modélisation proposé].
Estimer, à l'aide d'un modèle simple, le nombre de photons incidents nécessaires pour réceptionner 1 photon en retour après réflexion au point subterrestre.
Une puissance d'émission de 2 MW vous étonne-t-elle ?
[l'impulsion radar incidente est très brève : 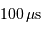 ; on se contentera également d'un ordre de grandeur grossier]
; on se contentera également d'un ordre de grandeur grossier]
La diffraction conduit à un lobe d'antenne de taille angulaire commensurable 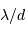 .
.
Pour le flux réfléchi : proposer un modèle simple pour les conditions de réflexion au point subterrestre.
 Spectres observé et théorique
Spectres observé et théorique
Difficulté : ☆
Temps : 10 min
La figure ci-jointe donne une portions des spectres observé et théorique d'une étoile de type F2, classe V.
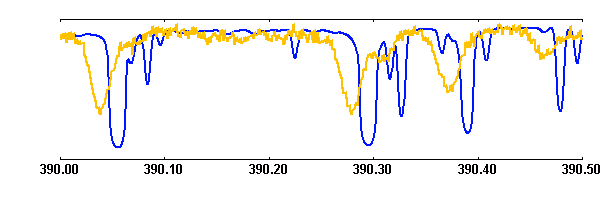
Spectres théorique (bleu) et observé (orange)
Crédit :
ESO/ASM
Question 1)
Expliquer les différences entre les 2 spectres
[1 points]
Question 2)
Donner un ordre de grandeur de 2 vitesses caractéristiques du spectre observé.
[2 points]
- Question 1
Aide :
L'onde radio parcourt le vide à la célérité de la lumière.
Attention au doublement de la distance par aller-retour.
Solution :
Un trajet de 616.125 s correspond à une distance aller-retour de 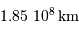 , soit 0.616 UA. On en déduit que Mercure est très proche de la ligne Soleil-Terre, à une distance minimale d'approche de la Terre.
, soit 0.616 UA. On en déduit que Mercure est très proche de la ligne Soleil-Terre, à une distance minimale d'approche de la Terre.
Dans ces conditions, Mercure est trop proche du Soleil pour être observé en lumière visible.
- Question 2
Aide :
Faire un schéma
Aide :
Un point 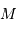 possède une vitesse de rotation
possède une vitesse de rotation 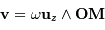
Solution :
La vitesse d'entraînement rotationnel vérifie :
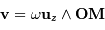
avec 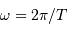 la rotation angulaire.
la rotation angulaire.
Soit, pour un point de coordonnées cartésiennes 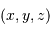 (avec bien sûr
(avec bien sûr 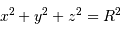 :
:
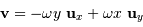
La projection radiale est la composante selon 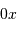 , càd
, càd 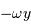
- Question 3
Aide :
Faire un schéma, avec les axes indiqués.
S'inspirer de l'animation sondage rotationnel .
Dans les applications numériques, ne pas oublie un facteur 2 temporel (aller-retour de l'onde) ou fréquentiel (double décalage Doppler à l'absorption et à la réémission de l'onde)
Solution :
La région de la surface hermienne contribuant au début du signal d'écho est le point le plus proche de la Terre : le point subterrestre. La fin correspond aux dernières régions touchées : au limbe.
La durée totale théorique 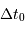 de l'écho correspond à l'intervalle de temps pour parcourir radialement la planète du point subterrestre au limbe, càd parcourir son rayon :
de l'écho correspond à l'intervalle de temps pour parcourir radialement la planète du point subterrestre au limbe, càd parcourir son rayon :
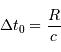
Les lignes d'iso-retard 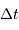 sur la carte
de Mercure [
sur la carte
de Mercure [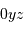 ] sont des lignes à coordonnée
] sont des lignes à coordonnée 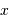 fixée. Analytiquement, à la surface de la planète et dans le plan du ciel
fixée. Analytiquement, à la surface de la planète et dans le plan du ciel 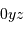 , l'équation
, l'équation
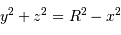
représente un cercle.
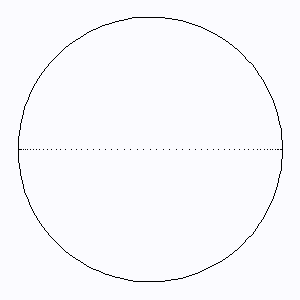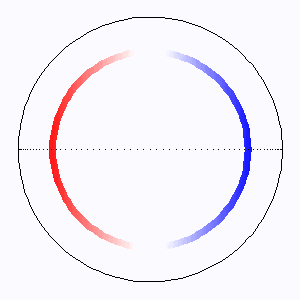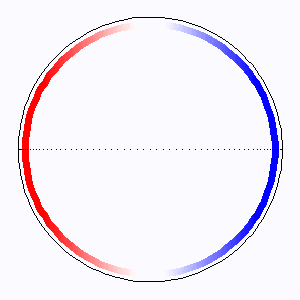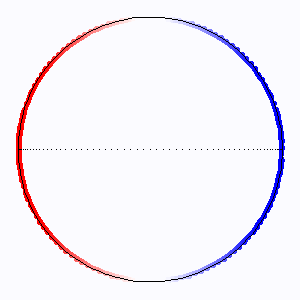
L'élargissement Doppler extrêmal est atteint au limbe, où l'entraînement rotationnel est le plus fort.
Les lignes d'iso-fréquence correspondent aux lignes isovitesses : ce sont des droites parallèles à l'axe de rotation.
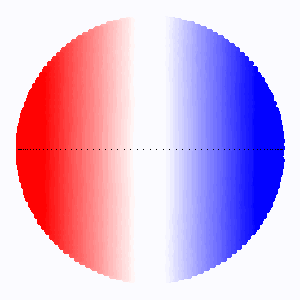 Pour un point de Mercure de coordonnées
Pour un point de Mercure de coordonnées
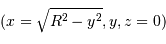 , le retard
, le retard 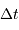 de l'écho et son décalage
spectral
de l'écho et son décalage
spectral 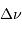 vérifient :
vérifient :
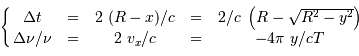
Les valeurs extrêmes du délai et du décalage sont :
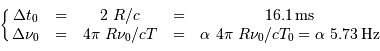
en ayant posé  .
On en déduit, pour un point du plan équatorial (
.
On en déduit, pour un point du plan équatorial (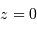 ) :
) :
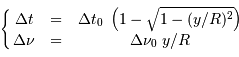
En éliminant la variable 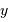 , il sort la relation demandée :
, il sort la relation demandée :
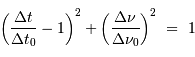
- Question 4
Aide :
Etudier les conditions de réflexion de l'onde, en supposant valide l'optique géométrique.
Aide :
Montrer que les dates effectives d'observations vérifient 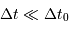 , et en tirer les conséquences.
, et en tirer les conséquences.
Aide :
Pour calculer 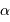 avec l'appliquette, la relation entre
avec l'appliquette, la relation entre 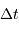 et
et 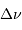 se traduit par :
= (B1/5.73) * sqrt(16.1 / (2*A1)), à faire calculer en ayant sélectionné la case C1
se traduit par :
= (B1/5.73) * sqrt(16.1 / (2*A1)), à faire calculer en ayant sélectionné la case C1
Solution :
Le retard maximal théorique est bien plus long que celui enregistré. Le
désaccord s'interprète par l'absence de signal réfléchi dans les régions proches du limbe.
Les lois de l'optique géométrique permettent d'interpréter les variations temporelles d'intensité du signal : la réflexion renvoie de moins en moins d'énergie vers la Terre dès lors que le signal s'éloigne du point subterrestre.
Et donc, les données présentant un grand retard par rapport au point subterrestre ne pas exploitables.
Les dates effectives d'observations vérifient alors 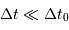 . Il s'ensuit que la relation entre
. Il s'ensuit que la relation entre 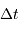 et
et 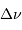 se simplifie en
se simplifie en
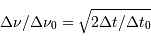
en ayant procédé au développement limité : 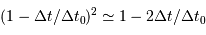 . Il en sort l'estimation de
. Il en sort l'estimation de 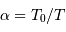 :
:
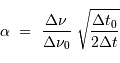
A l'aide de l'appliquette, on trouve 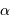 de l'ordre de 1.65, voisin de 5/3.
de l'ordre de 1.65, voisin de 5/3. 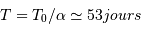 .
.
La rotation propre de Mercure est en résonance avec la révolution autour du Soleil. Mais elle est ici mesurée dans le référentiel tournant : la rotation propre sidérale découle du changement de référentiel, ici mesurée avec pour unité la révolution sidérale :
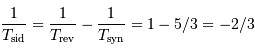
La rotation sidérale propre est plus lente que la révolution sidérale, est dans un rapport 3/2.
- Question 5
Aide :
La diffraction conduit à un lobe d'antenne de taille angulaire commensurable 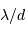 .
.
Aide :
Pour le flux réfléchi : proposer un modèle simple pour les conditions de réflexion au point subterrestre.
Solution :
La diffraction conduit à un lobe d'antenne de taille angulaire 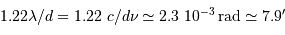 . En regard, Mercure intercepte une fraction angulaire
. En regard, Mercure intercepte une fraction angulaire 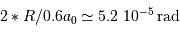 . La fraction du flux total intercepté par la planète est de l'ordre du rapport du carré de ces tailles angulaires, soit
. La fraction du flux total intercepté par la planète est de l'ordre du rapport du carré de ces tailles angulaires, soit 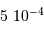 .
.




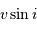 de 5, 20, 80 ou 200 km/s). Spectre d'une étoile F9 à grande résolution spectrale (R=120000)
de 5, 20, 80 ou 200 km/s). Spectre d'une étoile F9 à grande résolution spectrale (R=120000)

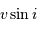 de 10, 80 ou 200 km/s. Spectre d'une étoile F9 à faible résolution spectrale (R=8000)
de 10, 80 ou 200 km/s. Spectre d'une étoile F9 à faible résolution spectrale (R=8000)
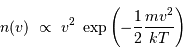
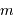 la masse atomique moyenne et
la masse atomique moyenne et 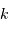 la constante de Boltzmann.
la constante de Boltzmann.
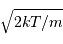 , du même ordre de grandeur que les vitesses moyenne ou la plus probable.
, du même ordre de grandeur que les vitesses moyenne ou la plus probable.

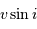 .
Les valeurs typiques de rotation varient de quelques km/s (rotateurs lents, tels le Soleil) à plusieurs centaines de km/s. Dans ce dernier cas, les signatures spectrales deviennent très peu marquées.
.
Les valeurs typiques de rotation varient de quelques km/s (rotateurs lents, tels le Soleil) à plusieurs centaines de km/s. Dans ce dernier cas, les signatures spectrales deviennent très peu marquées.

 . Lorsque l'axe de rotation de l'étoile se confond avec la ligne de visée, il n'y a pas d'élargissement rotationnel.
. Lorsque l'axe de rotation de l'étoile se confond avec la ligne de visée, il n'y a pas d'élargissement rotationnel.

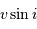 , et varie ici avec l'inclinaison
, et varie ici avec l'inclinaison  sur l'axe de visée.
sur l'axe de visée.
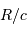 (
(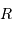 est le rayon de l'objet,
est le rayon de l'objet, 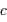 la célérité de la lumière) et donc scanne le champ de vitesse rotationnel.
la célérité de la lumière) et donc scanne le champ de vitesse rotationnel.



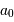
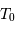
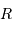
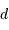
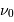

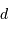 lors de l'observation,
et représenter la position relative de ces 2 planètes et du Soleil. Les observations effectuées pourraient-elles être menées en lumière visible ?
lors de l'observation,
et représenter la position relative de ces 2 planètes et du Soleil. Les observations effectuées pourraient-elles être menées en lumière visible ?
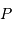 de la surface
visible de Mercure par ses coordonnées cartésiennes dans le repère
de la surface
visible de Mercure par ses coordonnées cartésiennes dans le repère
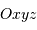 , où
, où 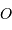 est le barycentre de la planète,
est le barycentre de la planète,
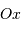 pointe vers la Terre et
pointe vers la Terre et 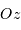 est parallèle à l'axe de rotation de la
planète. On note
est parallèle à l'axe de rotation de la
planète. On note 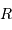 le rayon de la planète Mercure,
le rayon de la planète Mercure, 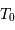 sa période de révolution sidérale, et
sa période de révolution sidérale, et 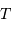 sa période de rotation propre.
sa période de rotation propre.
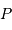 .
.
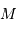 possède une vitesse de rotation
possède une vitesse de rotation 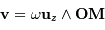
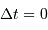 ) et à la fin (
) et à la fin (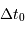 ) du signal d'écho.
Déterminer la durée totale théorique
) du signal d'écho.
Déterminer la durée totale théorique 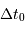 de l'écho ?
Représenter l'allure des lignes d'iso-retard
de l'écho ?
Représenter l'allure des lignes d'iso-retard 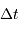 sur la carte
de Mercure [
sur la carte
de Mercure [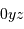 ].
].
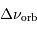 le décalage Doppler du signal
réfléchi au point subterrestre.
Quelles régions contribuent
à l'élargissement Doppler extrêmal
le décalage Doppler du signal
réfléchi au point subterrestre.
Quelles régions contribuent
à l'élargissement Doppler extrêmal
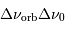 du signal ?
Représenter sur la carte de Mercure
l'allure des lignes d'iso-fréquence
du signal ?
Représenter sur la carte de Mercure
l'allure des lignes d'iso-fréquence 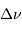 (à
(à 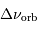 près).
près).
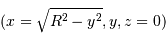 , le retard
, le retard 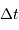 de l'écho et son décalage
spectral
de l'écho et son décalage
spectral 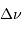 . Montrer que l'on a :
. Montrer que l'on a :
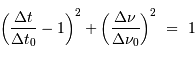
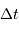 et
et 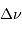 se réduit, pour les mesures effectuées, à
se réduit, pour les mesures effectuées, à 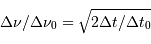 Comment interpréter les variations temporelles d'intensité du signal ?
Comment interpréter les variations temporelles d'intensité du signal ?
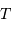 , la période de rotation propre de Mercure.
, la période de rotation propre de Mercure.
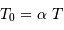 . Quelle signification donner à
. Quelle signification donner à 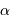 ?
De quelle fraction simple
?
De quelle fraction simple 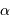 est-il proche ? Est-ce un hasard ?
est-il proche ? Est-ce un hasard ?
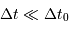 , et en tirer les conséquences.
, et en tirer les conséquences.
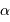 avec l'appliquette, la relation entre
avec l'appliquette, la relation entre 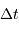 et
et 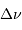 se traduit par :
se traduit par :
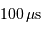 ; on se contentera également d'un ordre de grandeur grossier]
; on se contentera également d'un ordre de grandeur grossier]
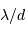 .
.

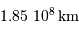 , soit 0.616 UA. On en déduit que Mercure est très proche de la ligne Soleil-Terre, à une distance minimale d'approche de la Terre.
, soit 0.616 UA. On en déduit que Mercure est très proche de la ligne Soleil-Terre, à une distance minimale d'approche de la Terre.
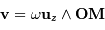
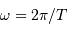 la rotation angulaire.
la rotation angulaire.
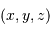 (avec bien sûr
(avec bien sûr 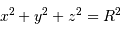 :
:
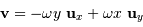
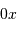 , càd
, càd 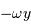
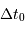 de l'écho correspond à l'intervalle de temps pour parcourir radialement la planète du point subterrestre au limbe, càd parcourir son rayon :
de l'écho correspond à l'intervalle de temps pour parcourir radialement la planète du point subterrestre au limbe, càd parcourir son rayon :
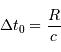
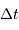 sur la carte
de Mercure [
sur la carte
de Mercure [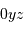 ] sont des lignes à coordonnée
] sont des lignes à coordonnée 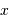 fixée. Analytiquement, à la surface de la planète et dans le plan du ciel
fixée. Analytiquement, à la surface de la planète et dans le plan du ciel 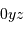 , l'équation
, l'équation
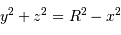

 Pour un point de Mercure de coordonnées
Pour un point de Mercure de coordonnées
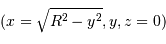 , le retard
, le retard 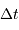 de l'écho et son décalage
spectral
de l'écho et son décalage
spectral 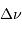 vérifient :
vérifient :
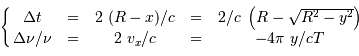
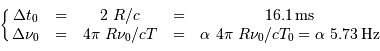
 .
On en déduit, pour un point du plan équatorial (
.
On en déduit, pour un point du plan équatorial (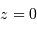 ) :
) :
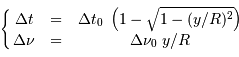
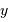 , il sort la relation demandée :
, il sort la relation demandée :
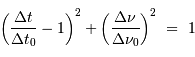
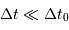 . Il s'ensuit que la relation entre
. Il s'ensuit que la relation entre 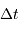 et
et 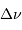 se simplifie en
se simplifie en
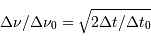
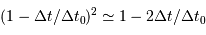 . Il en sort l'estimation de
. Il en sort l'estimation de 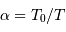 :
:
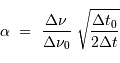
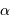 de l'ordre de 1.65, voisin de 5/3.
de l'ordre de 1.65, voisin de 5/3. 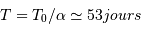 .
.
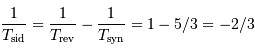
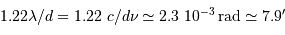 . En regard, Mercure intercepte une fraction angulaire
. En regard, Mercure intercepte une fraction angulaire 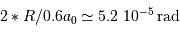 . La fraction du flux total intercepté par la planète est de l'ordre du rapport du carré de ces tailles angulaires, soit
. La fraction du flux total intercepté par la planète est de l'ordre du rapport du carré de ces tailles angulaires, soit 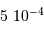 .
.