
|
Un référentiel, c'est aussi une horloge. La période apparente d'un phénomène périodique dépend donc de cette horloge.
Changer de référentiel, c'est changer de point de vue !
Comme ici, les différents référentiels concernés s'appuyant sur la rotation de la Terre autour du Soleil, ou sur la rotation de la Terre sur elle-même ou sur les étoiles fixes, sont en rotation angulaire les uns par rapport aux autres, il est nécessaire de s'intéresser à la composition des vitesses angulaires.
Les mesures d'une vitesse angulaire exprimée dans deux référentiels différents 1 et 2, identifiées par les indices /1 et /2, vérifient la "relation de Chasles" :
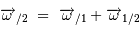
En considérant des mouvements de rotation coplanaires, l'égalité pour les périodes devient :
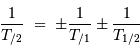
Les signes  dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
Dans les cas des référentiels terrestre tournant et sidéral, la rotation propre et la révolution étant le plus souvent sur des axes parallèles et dans le même sens, on a :
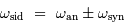
et donc :
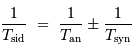
le signe 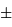 dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
Par exemple, on retrouve la relation entre le jour synodique moyen (temps qui sépare deux passages du Soleil au méridien) et le jour sidéral (temps pour que la Terre fasse un tour exact sur elle-même):
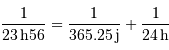
Ces 4 minutes de différence entre 23h56 et 24h00, en fait plutôt 3min56.3s, représente de l'ordre d'une fraction 1/365 de 24h.