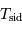QCM
Synodique ou sidéral
Difficulté : ☆
Temps : 20 min
Le tableau ci-joint donne les période de révolution sidérale des planètes du système solaire.
On veut calculer leurs périodes de révolution synodiques.
Périodes de révolution sidérale
| Planète |  |  |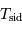
| UA | an |
| Mercure | 0.3871 | 0.2408 |
| Vénus | 0.7233 | 0.6152 |
| Terre | 1.0000 | 1.0000 |
| Mars | 1.5237 | 1.8808 |
| Jupiter | 5.2026 | 11.862 |
| Saturne | 9.5547 | 29.457 |
| Uranus | 19.218 | 84.020 |
| Neptune | 30.109 | 164.77 |
Question 1)
Le cas des planètes internes (Mercure, Vénus) est-il analogue à celui des planètes externes?
AideSolution
De la planète considérée et de la Terre,
qui double qui ?
La période synodique vérifie
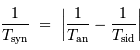
Question 2)
Calculer les révolutions synodiques.
Solution
Question 3)
Pourquoi les périodes synodiques ci-dessus calculées tendent-elles vers un an lorsque l'on s'éloigne dans le système solaire ?
Solution
Plus la planète est lointaine, plus son mouvement propre est lent, et donc son évolution se rapproche peu à peu de celle d'une étoile, animée essentiellement par le mouvement apparent dû à la rotation de la Terre autour du Soleil.
Ils tournent
Difficulté : ☆☆☆
Temps : 20 min
Question 1)
En quelle durée le Soleil parcourt-il son diamètre, du fait de la rotation diurne ?
AideSolution
Convertir l'unité angulaire en minute de temps
On peut arriver au résultat de 2 façons différentes.
Soit calculer la vitesse angulaire du soleil (360 degrés en 24 h,
15 degrés à l'heure), et donc un parcours de 0.5 deg prend 2 minutes.
Soit, directement, convertir le diamètre angulaire en diamètre horaire :
.
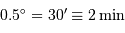Question 2)
En quelle durée la Lune parcourt-elle son diamètre ?
AideAideSolution
Estimer la part relative du mouvement propre de la Lune autour de la Terre et du mouvement d'entraînement dû à la rotation diurne.
Le mouvement propre de la Lune est-il vraiment important en 2 minutes ?
Comme la durée trouvée pour le Soleil est très courte devant la période
de révolution synodique de la Lune (29.5 j), alors que la Lune présente
le même diamètre angulaire que le Soleil, on peut négliger son mouvement.
Il s'ensuit que la durée cherchée est sensiblement
la même pour la Lune que pour le Soleil.
Question 3)
Déterminer la durée moyenne d'une éclipse, entre les premier et dernier
contacts ? La période de révolution synodique de la Lune est de 29.5 j ; les premier et dernier contacts correspondent aux tout début et toute fin de l'éclipse (situation 
et 
).
AideAideSolution
Montrer que 1 deg (2 diamètres solaires/lunaires) sépare le premier du
dernier contact.
Montrer que le fait de considérer la révolution synodique de la Lune
fige le mouvement du Soleil.
Pour "doubler" totalement le soleil, la lune doit
passer de la configuration 
à la configuration
, càd parcourir 2 diamètres, soit 1 deg.
Ceci représente 1/360ème de la période de révolution synodique (29.5 j),
soit 0.082 j, càd environ 2 heures.
Rotation de Mercure
Difficulté : ☆☆
Temps : 30 min
Question 1)
Déterminer la période sidérale de rotation, avec comme unité l'année hermienne
sidérale.
AideSolution
La question est peut être trop simple.
Si l'année hermienne vaut 1, le jour sidéral vaut 2/3, d'après l'énoncé, qui annonce 3 jours hermiens = 2 révolutions.
Question 2)
Définir les référentiels d'étude, et l'entraînement angulaire de l'un
par rapport à l'autre. Montrer alors que le jour hermien vaut 2 années sidérales.
AideSolution
Identifier ce qui est sidéral, hermien, et la révolution de l'un par rapport à l'autre.
En unités d'année hermienne sidérale, la période de rotation propre est 2/3, et la période d'entraînement du référentiel hermien par rapport aux étoiles est 1. La relation de cours, vue avec une période synodique, s'écrit ici avec la période hermienne cherchée :
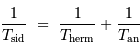
Avec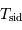 
la rotation hermienne sidérale,
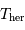Avec 
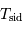la période hermienne sidérale, la rotation hermienne,
et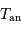 
l'année hermienne sidérale.
Donc, dans le système d'unité choisi :
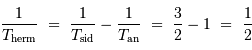
On en conclut que le jour hermien dure 2 années, comme l'illustre
l'animation.
S'exercer
