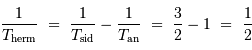Objectifs
Objectifs
Un référentiel, c'est aussi une horloge. La période apparente d'un phénomène périodique dépend donc de cette horloge.
Changer de référentiel, c'est changer de point de vue !
Comme ici, les différents référentiels concernés s'appuyant sur la rotation de la Terre autour du Soleil, ou sur la rotation de la Terre sur elle-même ou sur les étoiles fixes, sont en rotation angulaire les uns par rapport aux autres, il est nécessaire de s'intéresser à la composition des vitesses angulaires.
Composition des vitesses angulaires
Les mesures d'une vitesse angulaire exprimée dans deux référentiels différents 1 et 2, identifiées par les indices /1 et /2, vérifient la "relation de Chasles" :
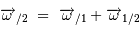
En considérant des mouvements de rotation coplanaires, l'égalité pour
les périodes devient :
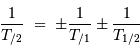
Les signes  dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
Sidéral versus synodique
Dans les cas des référentiels terrestre tournant et sidéral, la rotation propre et la révolution étant le plus souvent sur des axes parallèles et dans le même sens, on a :
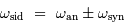
et donc :
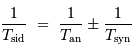
le signe 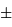 dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
Par exemple, on retrouve la relation entre le jour synodique moyen (temps qui sépare deux passages du Soleil au méridien) et le jour sidéral (temps pour que la Terre fasse un tour exact sur elle-même):
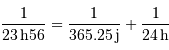
Ces 4 minutes de différence entre 23h56 et 24h00, en fait plutôt 3min56.3s, représente de l'ordre d'une fraction 1/365 de 24h.
Conversion
A l'aide de l'appliquette, convertir les périodes sidérales des planètes (Tsid) en périodes synodiques (Tsyn).

- Sélectionner la case C1, puis mener le calcul =1/(1-1/B1).
- Que se passe-t-il pour la Terre ? Sélectionner la case C3 et effacer le résultat.
- Pourquoi Mercure et Vénus se distinguent-elles ?
- Vers quelle période de révolution synodique tendent les planètes géantes ? Pourquoi ?
La rotation de Mercure
L'évolution de Mercure a conduit à figer ses périodes de rotation propre
et de révolution dans une résonance
de type 3:2, ce qui signifie que Mercure accomplit, dans un référentiel sidéral, 3 rotations
propres en 2 révolutions autour du Soleil.
Cette configuration particulière conduit, pour une hypothétique habitant
mercurien (hermien), à des jours valant deux années mercuriennes (voir
exercice), comme le montre
l'animation.
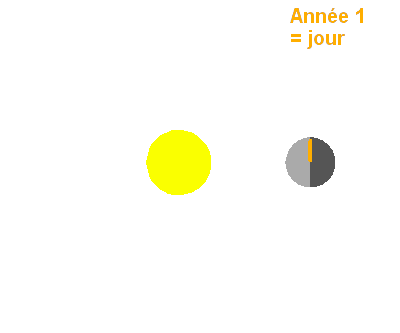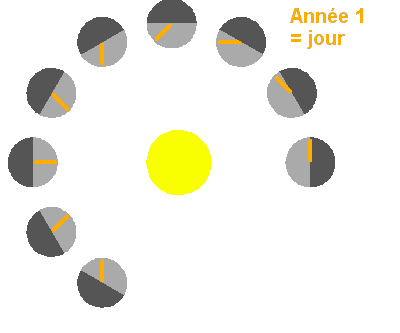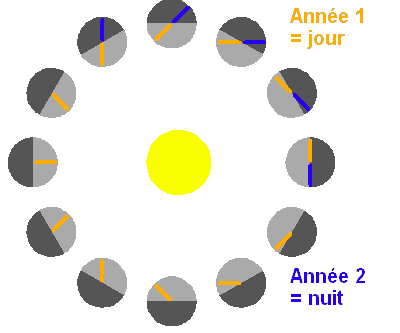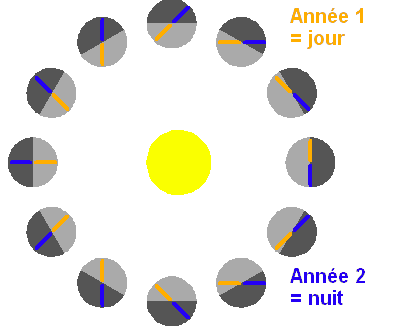
L'observateur est repéré par un tiret, jaune puis bleu. L'emploi de deux couleurs permet
de distinguer les 2 années nécessaires pour accomplir un jour sur
Mercure (ici défini entre 2 levers de Soleil).
Crédit :
ASM
 Synodique ou sidéral
Synodique ou sidéral
Difficulté : ☆
Temps : 20 min
Le tableau ci-joint donne les période de révolution sidérale des planètes du système solaire.
On veut calculer leurs périodes de révolution synodiques.
Périodes de révolution sidérale
| Planète |  | 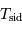 |
| UA | an |
| Mercure | 0.3871 | 0.2408 |
| Vénus | 0.7233 | 0.6152 |
| Terre | 1.0000 | 1.0000 |
| Mars | 1.5237 | 1.8808 |
| Jupiter | 5.2026 | 11.862 |
| Saturne | 9.5547 | 29.457 |
| Uranus | 19.218 | 84.020 |
| Neptune | 30.109 | 164.77 |
Question 1)
Le cas des planètes internes (Mercure, Vénus) est-il analogue à celui des planètes externes?
De la planète considérée et de la Terre,
qui double qui ?
Question 2)
Calculer les révolutions synodiques.
Question 3)
Pourquoi les périodes synodiques ci-dessus calculées tendent-elles vers un an lorsque l'on s'éloigne dans le système solaire ?
 Ils tournent
Ils tournent
Difficulté : ☆☆☆
Temps : 20 min
Question 1)
En quelle durée le Soleil parcourt-il son diamètre, du fait de la rotation diurne ?
Convertir l'unité angulaire en minute de temps
Question 2)
En quelle durée la Lune parcourt-elle son diamètre ?
Estimer la part relative du mouvement propre de la Lune autour de la Terre et du mouvement d'entraînement dû à la rotation diurne.
Le mouvement propre de la Lune est-il vraiment important en 2 minutes ?
Question 3)
Déterminer la durée moyenne d'une éclipse, entre les premier et dernier
contacts ? La période de révolution synodique de la Lune est de 29.5 j ; les premier et dernier contacts correspondent aux tout début et toute fin de l'éclipse (situation  et
et  ).
).
Montrer que 1 deg (2 diamètres solaires/lunaires) sépare le premier du
dernier contact.
Montrer que le fait de considérer la révolution synodique de la Lune
fige le mouvement du Soleil.
 Rotation de Mercure
Rotation de Mercure
Difficulté : ☆☆
Temps : 30 min
Question 1)
Déterminer la période sidérale de rotation, avec comme unité l'année hermienne
sidérale.
La question est peut être trop simple.
Question 2)
Définir les référentiels d'étude, et l'entraînement angulaire de l'un
par rapport à l'autre. Montrer alors que le jour hermien vaut 2 années sidérales.
Identifier ce qui est sidéral, hermien, et la révolution de l'un par rapport à l'autre.
 Le cas de la Lune
Le cas de la Lune
Difficulté : ☆☆
Temps : 20 min
La période de révolution synodique de la Lune, durée s'écoulant entre deux nouvelles lunes, vaut 29 j 12 h 44 min.
Question 1)
Calculer la période de révolution sidérale de la Lune.
[2 points]
Quelle rotation distingue les descriptions sidérale et synodique ?
Question 2)
Déterminer l'intervalle de temps moyen entre 2 passages consécutifs de la Lune au méridien.
[2 points]
La Lune n'est ni le Soleil, autour duquel la Terre tourne, ni les étoiles, considérées comme lointaines et fixes.
- Question 1
Aide :
Convertir l'unité angulaire en minute de temps
Solution :
On peut arriver au résultat de 2 façons différentes.
Soit calculer la vitesse angulaire du soleil (360 degrés en 24 h,
15 degrés à l'heure), et donc un parcours de 0.5 deg prend 2 minutes.
Soit, directement, convertir le diamètre angulaire en diamètre horaire :
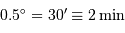 .
.
- Question 2
Aide :
Estimer la part relative du mouvement propre de la Lune autour de la Terre et du mouvement d'entraînement dû à la rotation diurne.
Aide :
Le mouvement propre de la Lune est-il vraiment important en 2 minutes ?
Solution :
Comme la durée trouvée pour le Soleil est très courte devant la période
de révolution synodique de la Lune (29.5 j), alors que la Lune présente
le même diamètre angulaire que le Soleil, on peut négliger son mouvement.
Il s'ensuit que la durée cherchée est sensiblement
la même pour la Lune que pour le Soleil.
- Question 3
Aide :
Montrer que 1 deg (2 diamètres solaires/lunaires) sépare le premier du
dernier contact.
Aide :
Montrer que le fait de considérer la révolution synodique de la Lune
fige le mouvement du Soleil.
Solution :
Pour "doubler" totalement le soleil, la lune doit
passer de la configuration  à la configuration
à la configuration
 , càd parcourir 2 diamètres, soit 1 deg.
, càd parcourir 2 diamètres, soit 1 deg.
Ceci représente 1/360ème de la période de révolution synodique (29.5 j),
soit 0.082 j, càd environ 2 heures.
- Question 1
Aide :
La question est peut être trop simple.
Solution :
Si l'année hermienne vaut 1, le jour sidéral vaut 2/3, d'après l'énoncé, qui annonce 3 jours hermiens = 2 révolutions.
- Question 2
Aide :
Identifier ce qui est sidéral, hermien, et la révolution de l'un par rapport à l'autre.
Solution :
En unités d'année hermienne sidérale, la période de rotation propre est 2/3, et la période d'entraînement du référentiel hermien par rapport aux étoiles est 1. La relation de cours, vue avec une période synodique, s'écrit ici avec la période hermienne cherchée :
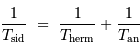
Avec 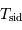 la rotation hermienne sidérale,
la rotation hermienne sidérale,
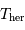 Avec
Avec 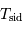 la période hermienne sidérale, la rotation hermienne,
et
la période hermienne sidérale, la rotation hermienne,
et 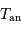 l'année hermienne sidérale.
l'année hermienne sidérale.
Donc, dans le système d'unité choisi :
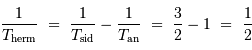
On en conclut que le jour hermien dure 2 années, comme l'illustre
l'animation.
 Objectifs
Objectifs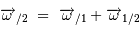
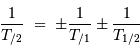
 dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
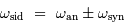
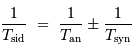
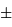 dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
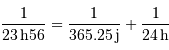

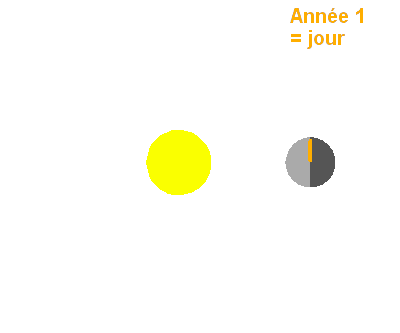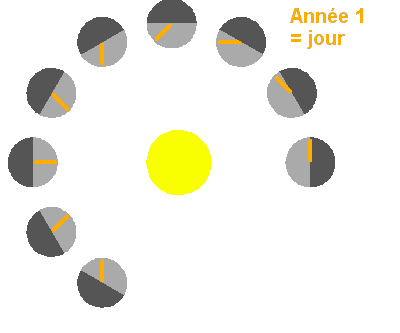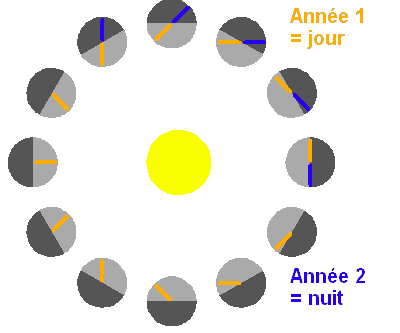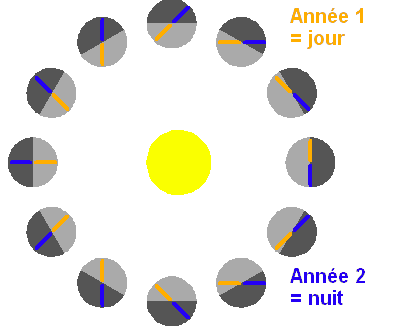
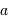
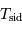
 et
et  ).
).
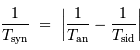
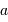
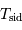
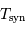
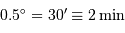 .
.
 à la configuration
à la configuration
 , càd parcourir 2 diamètres, soit 1 deg.
, càd parcourir 2 diamètres, soit 1 deg.
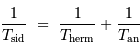
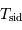 la rotation hermienne sidérale,
la rotation hermienne sidérale,
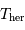 Avec
Avec 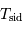 la période hermienne sidérale, la rotation hermienne,
et
la période hermienne sidérale, la rotation hermienne,
et 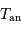 l'année hermienne sidérale.
l'année hermienne sidérale.