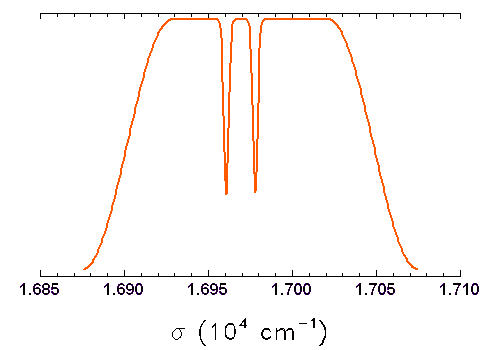
Le filtre sélectionne ici 2 raies (les raies modélisées du doublet du sodium). La variable spectrale est donnée en nombre d'onde
.
Crédit :
ASM
Au fil de l'interférogramme
Un interférogramme présente une modulation, de période égale à la longueur d'onde moyenne sélectionnée par le filtre.
Interférogramme du
spectre synthétique du sodium. Le domaine spectral étant large, le contraste décroît avec la longueur d'onde. Les oscillations ont pour période moyenne 589.3 nm.
Crédit :
ASM
L'interférogramme présente à plus grande différence de marche des motifs liés à la nature du signal.
A très grande différence de marche, il perd tout contraste.
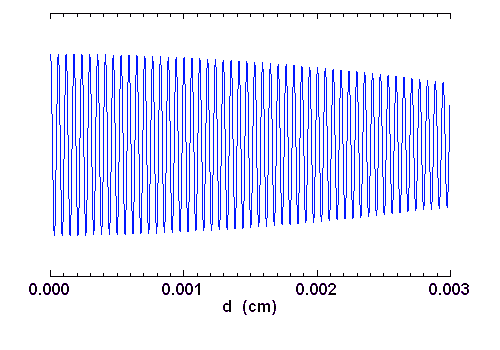
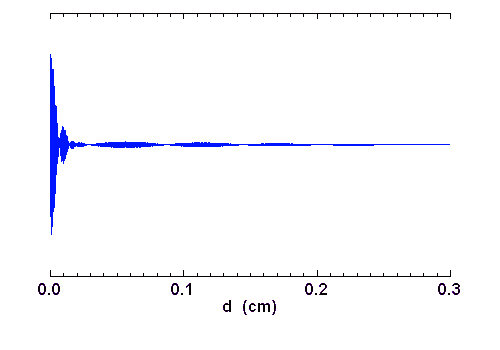
Interférogramme du
spectre
synthétique du sodium. Les motifs sont dus au doublet du
sodium. Leur effacement à grande différence de marche provient de la non-cohérence du signal spectral : les raies du sodium présentent une certaine largeur, càd une longueur de cohérence limitée. A l'échelle de cet interférogramme, la modulation présente lorsque l'on zoome sur une
portion de l'interférogramme n'est plus
visible ; on visualise ici essentiellement l'enveloppe du signal, qui représente les variations du
contraste.
Crédit :
ASM
Crédit :
ASM
 Objectifs
Objectifs
Introduire la notion de contraste, qui rend compte d'une
modulation amoindrie dans l'interférogramme d'une raie réelle, qui
n'est pas strictement monochromatique.
Le contraste représente globalement l'allure de l'interférogramme,
avec des trains de franges plus ou moins contrastés (chaque frange
n'étant localement qu'essentiellement un bout de sinusoïde de
période égale à la longueur d'onde moyenne sélectionnée par le
filtre d'entrée.
Monochromaticité
Un laser présente une bonne réalisation pratique d'une raie monochromatique. Sa longueur de cohérence peut être tellement grande que la réalisation de son interférogramme conduit effectivement à un signal également modulé à toute différence de marche :
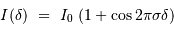
Mais une source réelle ne présente pas un telle cohérence (autrement dit, elle est moins monochromatique), et cela modifie les propriétés de l'interférogramme, qui apparaît moins contrasté.
Définition du contraste
Le contraste se mesure localement dans l'interférogramme par :
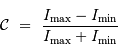
Dans l'interférogramme d'une source avec une seule raie plus ou moins large,
il intervient comme :
![I (\delta) \ = \ I_0 \ \left[ 1 + { \mathcal{C}} (\delta) \cos(2\pi\sigma\delta)\right]](../pages_fourier/equations_fts-frange/equation6.png)
Visibilité des franges d'interférence
La visibilité des franges, ou leur contraste, dépend de la largeur des raies du spectre. Une approche simple est proposée en exercice.
Des animations montrent comment la visibilité évolue avec la largeur des raies, mais aussi avec la largeur du filtre.
Visibilité
La visibilité des franges dépend de la largeur spectrale des raies étudiées. Plus les raies sont larges, moins les franges sont visibles à grande différence de marche.
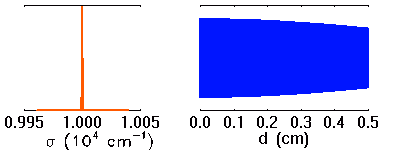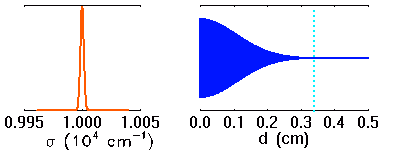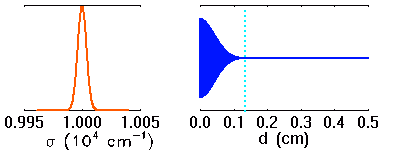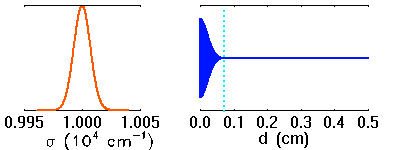
Simulation d'une raie en émission, et interférogramme associé. Lorsque la raie s'élargit, les motifs interférométriques à différence de marche élevée disparaissent.
Crédit :
ASM
 Visibilité des franges
Visibilité des franges
Difficulté : ☆☆☆
Temps : 45 min
On alimente un spectromètre par TF par un spectre avec une seule raie, non monochromatique, de largeur
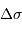 . On note
. On note 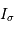 l'intensité spectrale, et
l'intensité spectrale, et 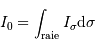 l'intensité dans la raie.
Pour simplifier les calculs, on ne s'intéresse pas à un profil réaliste,
mais à un profil de raie en émission idéalisé par :
l'intensité dans la raie.
Pour simplifier les calculs, on ne s'intéresse pas à un profil réaliste,
mais à un profil de raie en émission idéalisé par :
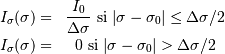
Question 1)
Justifier le fait que l'intensité totale 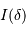 enregistrée à la différence de marche
enregistrée à la différence de marche 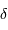 est la somme de toutes les intensités spectrales reçues.
est la somme de toutes les intensités spectrales reçues.
[3 points]
Question 2)
Mener le calcul de l'interférogramme.
[3 points]
Question 3)
Montrer la relation :
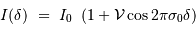
et exprimer la fonction de visibilité des franges 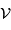 en fonction de
en fonction de
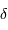 et
et 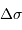 .
.
[1 points]
Question 4)
Représenter schématiquement la fonction
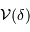 .
Déterminer la première valeur
.
Déterminer la première valeur 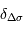 qui annule la fonction de visibilité.
qui annule la fonction de visibilité.
[2 points]

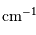 .
.



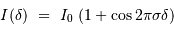
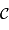 des franges est le rapport entre l'amplitude de modulation de la frange à l'énergie totale
des franges est le rapport entre l'amplitude de modulation de la frange à l'énergie totale 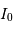 collectée dans le filtre.
collectée dans le filtre.
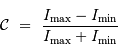
![I (\delta) \ = \ I_0 \ \left[ 1 + { \mathcal{C}} (\delta) \cos(2\pi\sigma\delta)\right]](../pages_fourier/equations_fts-frange/equation6.png)

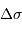 . On note
. On note 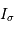 l'intensité spectrale, et
l'intensité spectrale, et 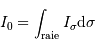 l'intensité dans la raie.
Pour simplifier les calculs, on ne s'intéresse pas à un profil réaliste,
mais à un profil de raie en émission idéalisé par :
l'intensité dans la raie.
Pour simplifier les calculs, on ne s'intéresse pas à un profil réaliste,
mais à un profil de raie en émission idéalisé par :
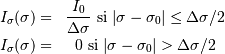
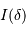 enregistrée à la différence de marche
enregistrée à la différence de marche 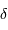 est la somme de toutes les intensités spectrales reçues.
est la somme de toutes les intensités spectrales reçues.
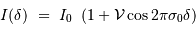
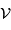 en fonction de
en fonction de
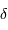 et
et 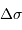 .
.
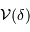 .
Déterminer la première valeur
.
Déterminer la première valeur 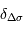 qui annule la fonction de visibilité.
qui annule la fonction de visibilité.