S'évaluer

Visibilité des franges

Difficulté : ☆☆☆ Temps : 45 min

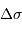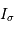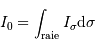On alimente un spectromètre par TF par un spectre avec une seule raie, non monochromatique, de largeur $\Delta\sigma$ . On note $I_\sigma$ l'intensité spectrale, et $I_0 = \int _{\mathrm{raie}} I_\sigma {\mathrm{d}} \sigma$ l'intensité dans la raie. Pour simplifier les calculs, on ne s'intéresse pas à un profil réaliste, mais à un profil de raie en émission idéalisé par :

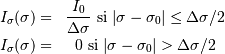
$\begin{eqnarray*} I_\sigma (\sigma) =& \displaystyle{I_0\over \Delta \sigma} \mathrm{ \ si\ } |\sigma-\sigma_0| \le \Delta\sigma/2\\ I_\sigma (\sigma) =& 0 \mathrm{ \ si\ } |\sigma-\sigma_0| > \Delta\sigma/2 \end{eqnarray*}$

Question 1)

Justifier le fait que l'intensité totale 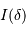$I(\delta)$ enregistrée à la différence de marche 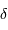$\delta$ est la somme de toutes les intensités spectrales reçues.

[3 points]

Question 2)

Mener le calcul de l'interférogramme.

[3 points]

Question 3)

Montrer la relation :

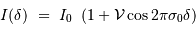
$I( \delta) \ = \ I_0\ \left(1 + { \mathcal{V}} \cos 2\pi\sigma_0 \delta \right)$

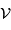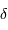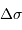et exprimer la fonction de visibilité des franges $\mathcal{V}$ en fonction de $\delta$ et $\Delta\sigma$ .

[1 points]

Question 4)

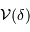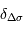Représenter schématiquement la fonction ${ \mathcal{V}} ( \delta )$ . Déterminer la première valeur $\delta_{\Delta\sigma}$ qui annule la fonction de visibilité.

[2 points]