Apprendre

L'intervalle spectral libre contient entièrement le domaine spectral : il est suffisamment large, et les 2 bornes du signal sont comprises dans le même segment multiple de l'intervalle spectral.

Crédit : ASM

L'intervalle spectral libre ne contient pas entièrement le domaine spectral. Le principe de la spectrométrie par TF est alors inopérant.

Crédit : ASM

Avec 163 points, l'interférogramme est convenablement échantillonné, et l'intervalle spectral libre inclut toutes les données. Ce n'est pas le cas avec 162 ou 164 points : le nombre de points inadapté conduit à un mauvais repliement du spectre.

Crédit : ASM

Le spectre initial est mieux reproduit lorsque l'interférogramme est obtenu avec une grande différence de marche maximale. Sur cet exemple, la résolution du spectre initial est reproduite avec un balayage de l'interférogramme jusqu'à 4 cm (R = 68000), alors que 0.1 ou 1.0 cm restent insuffisants (respectivement R = 1700 et 17000).

Crédit : ASM

Suréchantillonner ne sert à rien. Il n'y a pas plus d'information dans l'interférogramme à 1630 points que dans celui à 163.

Crédit : ASM

Objectifs

Décortiquer le fonctionnement d'un spectromètre par transformée de Fourier, en s'appuyant sur les propriétés d'une TF en lien avec les caractéristiques souhaitées du spectre.

Simulations

Une observation par spectrométrie de Fourier nécessite le choix de paramètres de Fourier efficaces pour l'enregistrement rapide de l'interférogramme. La comparaison entre le spectre initial et le spectre calculé à partir d'un interférogramme simulé permet de jauger la pertinence des choix effectués.

Principe... et propriétés de la TF discrète.

L'interférogramme, obtenu par pas de différences de marche équidistants de 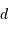, admet une fréquence de coupure 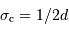$\sigma _{\mathrm{c}}=1/2d$ . La valeur de cette fréquence, donc la valeur de 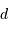, ne peuvent pas être prises au hasard.

Le spectre étant recalculé à partir de l'interférogramme par transformée de Fourier rapide (fft), la validité du principe suppose que les bornes de l'intervalle spectral libre, multiples entiers consécutifs de 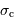$\sigma _{\mathrm{c}}$ , encadrent entièrement le domaine spectral défini par le filtre d'entrée.

Intervalle spectral libre

Quand bien même la largeur de l'intervalle spectral libre est suffisante, mais avec un spectre distribué sur 2 intervalles, le résultat ne sera pas correct, par suite du repliement des fréquences lors de la fft. Le nombre de points de l'interférogramme doit être optimisé. S'il diffère légèrement de la valeur optimale, le mauvais échantillonnage du signal conduit à retrouver un spectre à l'aspect tordu, par suite du repliement indu de fréquences mal séparées.

Résolution spectrale

La résolution spectrale varie en fonction de la différence de marche maximale 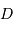explorée. Elle s'exprime simplement :

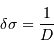
$\delta\sigma = {1\over D}$

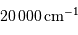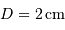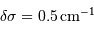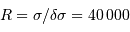Exemple : pour une raie à $20\,000 {\,\mathrm{cm}}^{-1}$ et $D = 2 {\,\mathrm{cm}}$ , $\delta\sigma = 0.5 {\,\mathrm{cm}}^{-1}$ et le pouvoir de résolution vaut donc $R = \sigma / \delta\sigma = 40\,000$ .

Echantillonnage

Rien ne sert de suréchantillonner l'interférogramme dès lors que le nombre de points 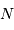a été optimisé au sens des propriétés de la transformée de Fourier rapide.